一、二项式实例
为了让读者更了解二项式定价法及蒙特卡罗仿真法的定价原理，本节特别以两个实例说明。读者可以利用所熟悉的Excel软件，根据本书介绍的步骤，求出期权的价值，相信将有助于对这两种定价方法的了解。
【例题4】 假设股价S=100，执行价格K=100，股价报酬率波动率σ=60%，无风险利率r=6%，期权到期期限T=1年，期数分割为n=5期，求看涨期权的价格。
解: 由以上条件，我们知道σ=60%，Δt=1/5=0.2，因此u=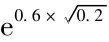
=1.3078
则
因此，先将股价展开成5期的树形图，如图18-4。由对应的到期的股价，我们便可以得知到期看涨期权的价值(如图18-4)。譬如，股价为382.53元时，到期看涨期权价值为282.53元。然后，再依公式18-1逐渐往左推出前一期看涨期权的价值，最后我们便可以得到欧式看涨期权价格为26.98元，其计算出来的值如图18-5。随着切割期数的增加，求出的看涨期权价值会愈接近理论值，如图18-6所示，大约在分割期数为50期时，便接近理论价格25.92元。
图18-4 二项式股价树形图(股价的展开)
图18-5 二项式看涨期权计算方法(期权的回推)(www.xing528.com)
图18-6 二项式价格收敛图
二、蒙特卡罗仿真法实例
【例题5】 假设给定同样的条件，亦即股价S=100，执行价格K=100，股价报酬波动率σ=60%，无风险利率r=6%，期满日T=1年，求看涨期权价值。
解: 首先，我们假设Δt=1，即股价1年产生一次，并以抽样10次为例。首先我们可以在Excel中输入=NORMSINV(RAND())，便可以得到10个正态分布随机数，根据公式18-4产生最后10个股价。
随后，我们将抽到的10个随机数及其产生的股价在表18-1列出，以第一次抽到随机数0.6534为例，到期股价为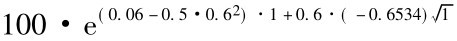
=59.93，因为此次路径股价小于100，所以到期看涨期权价值为0。重复以上步骤，便可以知道10个看涨期权的到期价值，再将这10个看涨期权的价值平均，得到39.04元，然后再以6%的利率折现，得到10次模拟的看涨期权现值为36.83元，如表18-1。随着抽样次数的增加，看涨期权的现值会逐渐接近理论值25.92元。[5]
表18-1 蒙特卡罗模拟法(10次)
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
