二项式期权定价模型分析与优化

二项式期权定价模型(binomial option pricing model，BOPM)是一种常用来给期权定价的方法。在二项式定价模型中，由于股价展开以后，成为倾倒90度角的树状，因此也常称为二项树状模型(binomial tree model)或树状模型(tree model)或二项式模型。二项式模型最早是由诺贝尔奖得主William Sharpe在1978年提出，后来John Cox、Stephen Ross和Mark Rubinstein三人以及Rendleman和Barter两人又分别提出相同主张。目前大都以Cox、Ross和Rubinstein三人发表的论文为主，故又称为CRR模型。[1]

二项式模型的基本概念是假设股价的变动是间断的(discrete)，而非B-S模型中的连续的(continuous)。二项式模型中假设股价不是涨到Su就是下跌至Sd两种情形，其中S为股价，u、d为1加上上涨幅度或减去下跌幅度。譬如上涨10%，则u=1.1; 下跌10%，则d=0.9，即股价不是由100上涨到110=100×1.1，就是下跌到90=100×0.9。

二项式模型是借由求出最终股价，然后求出最终期权价格，再往前推出二项式模型前一期的期权价格，再通过相同程序，求出更往前一期的价格，如此重复，最后得出期权的期初价格。因此，二项式模型基本上是知道了期满日的股价，推导出到期期权价格，再推回期初的看涨期权价格。

首先，假设期权还有一期到期，股价上涨到Su或下跌到Sd，假设看涨期权到期的价格分别为Cu和Cd，而Cu等于max(Su－K，0)，而Cd等于max(Sd－K，0)，如图18－1所示。

图18-1 一期模型

因此，二项式一期期初看涨期权价值的公式可以得到如下:

其中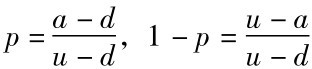，，a=erΔt或1+rΔt，r为利率;Δt为期间的长短。此外， u、a、d还须满足u＞a＞d的条件，不然会有套利的情形发生。在此，p可视为股价上涨的概率。[2]

【例题1】 假设目前股价为S=100，看涨期权执行价格K=100，还有1年到期，另假设u=1.2，d=0.9，年利率为10%，求此看涨期权的价格。(www.xing528.com)

解: 一年后可能股价:

上涨: Su=100×1.2=120

下跌: Sd=100×0.9=90

股价上涨时，看涨期权到期值Cu=max(120－100，0) =20。

股价下跌时看涨期权到期值Cd=max(90－120，0) =0。

而Δt=1，所以a=erΔt=e0.1×1=1.1，而p=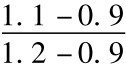=0.667，1－p=0.333，代入公式得到目前看涨期权价值为:

C=(0.667×20+0.333×0)/a=(0.667×20)/1.1=12.1