Black-Scholes公式解析与优化技巧

B-S公式虽看起来很复杂，包括自然对数、标准常态累积概率等，但实际上包含很多简单而实用的信息，以下将分别解释说明。

一、N(d1)为对冲比率

B-S公式中的N(d1)一般称为对冲比率或避险比率(hedge ratio)，或delta。即:

其中: ΔC: 看涨期权变动的大小

ΔS: 股价变动的大小[5]

这个比率表示认购权证或看涨期权对股价变动的变动比值。譬如在中国石油的例子中，N(d1) =0.655，表示股价上涨1元，看涨期权或认购权证理论上将上涨0.655元;反之，股价下跌1元，看涨期权或认购权证理论上将下跌0.655元。所以，券商卖出一股认购权证时，如果股价上涨，认购权证价格上涨，券商就会遭受损失，因此需要买入0.655股股票，才可以“规避”或“对冲”因股价上涨而面临的损失风险，故N(d1)又称为对冲比率或对冲率。如果股价上涨1元，认购权证上涨0.655元，券商就会损失0.655元，而买入的0.655股股票，刚好获利0.655元。如此一来，便可将股价上涨造成的认购权证损失的风险完全对冲掉; 反之，股价下跌情形亦类似。

二、N(d1)不固定

B-S公式中的N(d1)不是固定的，而是会随着股价的上涨而上升、随着股价下跌而下降。因为由公式5-1可知，股价上涨，那么d1上升，N(d1)也会上升; 反之，当股票价格下跌，那么d1下降，N(d1)也会下降。所以，随着股价的变动，券商的对冲比率，即买入股票的数量也会变动，也就是对冲比率会随时调整。实务上，因为随时调整N(d1)较不可行，一般而言，券商发行权证对冲时会订定一个对冲比率的上下区间，只要不超过此区间就不用一直调整对冲比率。

三、N(d1)为切线斜率

N(d1)也是看涨期权和股价关系图形的切线斜率，因为股价变动引起看涨期权变动的大小的比例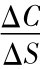，在数学式的意义就是切线的斜率。随着股价的上涨，切线斜率将增加，最高到45°，此时切线斜率为1; 随着股价下跌，切线斜率将下降，最极端的状况为水平切线，此时切线斜率为0，如图5-2所示。

图5-2 股价、看涨期权价值及对冲比率

说明:虚线部分表示切线的斜率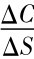。切线斜率即对冲比率，切线斜率最大为45°，斜率为1; 切线斜率最小为0，为水平线。

四、N(d1)介于0和1之间[6]

另外，由概率的概念来看，N(d1)会介于0和1之间，亦即0≤N(d1)≤1。因为N(d1)为一累积概率，所以累积概率最低为0，最高为1。也就是说股价上涨1元，看涨期权最低上涨0元，最高上涨1元。我国台湾证券交易所对认购权证涨跌幅的限制，基本上是假设N(d1)为1，也就是股价上涨1元，权证最多上涨1元; 反之，股价下跌1元，权证最多下跌1元。因此，认购权证的涨跌大小，便是以目标股价的涨跌大小为范围。

譬如在台湾地区股市有7%涨跌停的限制，假设今天鸿海的收盘股价为100元，明日鸿海股价在7%的涨跌幅下为107元及93元，即上涨、下跌各7元。因此，根据台湾证券交易所的规定，明天认购权证的上涨、下跌也限制在7元。也就是说，如果今天认购权证收盘价格为20元，那么明天认购权证最高为27元，最低为13元。

另外，为了考虑执行比例不是1的情形，台湾证券交易所于1999年9月，将认购权证的涨跌停大小改为目标股价的7%再乘以执行比例。譬如执行比例如果是1.2，即每一股认购权证可以换1.2股目标股票，则认购权证的涨跌停为±7×1.2=±8.4元，即最大可以上涨至8.4元、下跌至8.4元。目前国内许多认购权证的执行比率小于1，因此权证的涨跌幅会小于股票的涨跌幅。

五、N(d1)可解释认购权证有助涨助跌的作用

N(d1)可以解释为什么认购权证的发行可能会有助涨助跌的效果。如果股价上涨， d1上升，N(d1)会上升，所以券商要买入更多股票来对冲，因此增加市场上对此一股票的需求，使股价更加上涨; 反之，如果股价下跌，N(d1)下降，券商要抛售股票减少对冲数量，因此会增加此一股票的供给，使股价更加下跌。

六、股价很高时，N(d1)=1; N(d2)=1(www.xing528.com)

当股价相对于执行价格很高时，N(d1)及N(d2)会逼近1，此时看涨期权公式变为C=S－K(1+r)－T，因而当股价上升1元时，看涨期权价值也会上升1元。此时看涨期权的价格性质和股票相似，不同的只是现在支付S－K(1+r)－T拿到看涨期权，届时再以K元换入股票。在此情形下，看涨期权价格等于看涨期权价格下限或广义的内在价值。

七、N(d1)和时间价值的关系

我们也可由N(d1)来解释第三章所提到的论点: 价内看涨期权，当股价上涨时，时间价值下降; 反之，价外看涨期权，当股价上涨时，时间价值会上升。我们知道，价内看涨期权的价值可以表示为内在价值(S－K)和时间价值(Time Value，TV)的和，即:

C=S－K+TV (5-2)

对公式5-2微分得到:

其中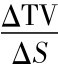=股价变动对时间价值的影响。

因为已知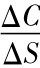=N(d1)，所以1+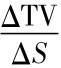=N(d1)。又因为N(d1)≤1，所以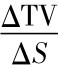＜0。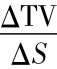＜0表示股价和时间价值的变动成相反方向，也就是表示股价上涨，价内看涨期权的时间价值将下降; 或者股价下跌时，价内看涨期权的时间价值上升。

对价外看涨期权而言，由于内在价值为0，所以看涨期权价值即时间价值(C=TV)，对看涨期权微分得到: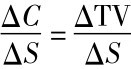=N(d1)，因为0≤N(d1)≤1，所以0≤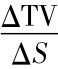≤1为正，而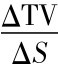＞0表示股价和时间价值成同向变动。所以，股价上涨，价外看涨期权的时间价值也会上升; 反之，股价下跌，价外看涨期权时间价值下跌。

八、N(d2)为到期时股价大于执行价格的概率

B-S公式的第二部分N(d2)，代表股价在期满日时会大于执行价格的概率。K(1+r)－T表示到期需支付K元的执行价格，以换取股票所换算成目前的现值。K(1+r)－TN(d2)则表示考虑了履约的概率后，预期将支出金额的现值，即预期成本的现值; 而SN(d1)则可视为是预期收益的现值。因此，预期收益现值SN(d1)减去预期成本现值，便是看涨期权预期价值的现值，即看涨期权目前的理论价值。

九、看涨期权可由股票和债券来复制

B-S公式也告诉我们，看涨期权其实可以藉由买入N(d1)股的股票及卖出K(1+r)－TN(d2)的债券来复制，也就是说看涨期权隐含融资K(1+r)－TN(d2)来买N(d1)股股票。这和第四章看跌看涨期权平价关系所提到的看涨期权可由买入股票及买入看跌期权来复制的概念很类似［C=S+P－K(1+r)－T］。不同的是，看跌看涨期权平价关系复制的看涨期权是期满日的报酬型态。因此，只要复制以后，就不要再调整; 而此处的看涨期权经由股票及债券来复制，则是短时间的报酬型态，因为N(d1)会随时改变，所以需要随时调整买入的股票数量来达到完全复制看涨期权的效果。

十、B-S公式也告诉我们C(nS，nK) =n·C(S，K)

假设有两支看涨期权A与B，其期满日、波动率及价内外程度(moneyness，定义为S/K)均相同，但是A看涨期权的股价及执行价格都是B看涨期权的n倍，那么A看涨期权的价格应该是B看涨期权价格的n倍。亦即:

C(nS，nK) =nC(S，K)

譬如例题1中，如果某一看涨期权的目标股价及执行价格均为200元，其余条件均相同，则该认购权证的价格应为2×25.78=51.56元。

动动脑

你会证明C(nS，nK) =nC(S，K)吗?