信用风险度量模型的优化

信用风险与市场风险相比，具有以下特性:其一，市场风险的概率分布通常近似服从正态分布。债务合约的信用风险有所不同，若贷款能安全收回，贷款人只可获得约定的利息，一旦债务人违约，则贷款人可能会损失全部或部分本金。由于贷款具有收益、损失不对称的特点，且损失区域的概率密度高于相应的正态分布的概率密度，即存在“厚尾”(fat tail)，使得信用风险的概率分布不适合于正态分布的假设，为引入统计分析带来困难。其二，借贷双方存在显著的信息不对称。借款人较贷款人掌握了更多的信息，可能产生道德风险问题。其三，信用风险的观察数据不易获取。贷款是非公开交易，难以观察到贷款的市场价值及其波动性。由于这些特性，信用风险的量化难度较大。

20世纪60年代以来，随着风险管理技术的进步，信用风险的测度逐步实现突破，发达国家的学者和机构陆续开发出各具特色的多种信用风险度量模型，基于风险评估模型的计量分析被引入银行的实践操作中。

(一)信用风险的度量要素

根据《巴塞尔资本协议Ⅱ》，信用风险的度量包括以下要素:一是违约概率(PD)，即借款人或交易对手无法履行其合约义务的概率；二是违约损失率(LGD)，指在借款人或交易对手发生违约事件的情况下，债权人或交易另一方遭受的损失程度；三是违约风险暴露(EAD)，是指债务人违约时预期表内和表外项目的风险暴露总额，包括已使用的授信余额、应收未收利息、未使用授信额度的预期提取数量以及可能发生的相关费用等。

将信用风险度量从狭义的违约风险扩展到广义的信用价差风险，需要测度信用等级迁移概率，即债务人在特定的时间内从期初信用等级迁移到各个信用等级的概率。如果要度量信贷组合的风险，还需估算借款人之间的违约相关性或联合信用等级迁移概率，即信贷组合中借款人的违约风险或信用品质变化之间的关联程度。

(二)基于财务指标的信用风险度量模型

20世纪60年代至80年代，学术界创建了基于财务比率评估企业信用风险的若干模型，其中具有代表性的模型如下:

1．Z计分模型

Z计分模型是由美国学者阿尔特曼(Altman)于1968年创建的信用评分模型，其基本思路是:采用多元线性判别分析法，从备选的多项财务比率中筛选出对企业破产风险最具判别能力的财务比率，分别赋予这些比率在综合评分中的权重，建立一个区分破产与非破产企业的判别函数，据此计算出企业的Z分值(Z-score)，将之与临界值比较，以判别其破产的可能性。

该方法涉及三个关键环节:一是选择财务比率，二是各比率的权重分配，三是临界值的确定。Altman选取了5个财务比率，分别是:营运资本/总资产(X1)、留存收益/总资产(X2)、税息前利润/总资产(X3)、权益市值/总负债(X4)、销售收入/总资产(X5)，分别反映企业的偿债能力、盈利能力、财务结构和营运能力，构建五变量Z值计分模型，其公式如下:

Z＝0．012X1＋0．014X2＋0．033X3＋0．006X4＋0．999X5

其后，设定判别函数的临界值，破产区域的上限值为1．81，非破产区域的下限值为2．99，中间是灰色区域。通过计算Z分值，观察其落在哪一段区域，预测企业是否会破产。如果企业的Z分值高于2．99，信用状况良好；如果Z分值低于1．81，企业发生财务危机的可能性较大；如果Z分值落在灰色区域，模型不能判别企业是否会破产。

和传统的定性分析相比，Z计分模型的优点是相对客观且量化，其局限性在于:线性判别函数可能不能充分描述各因素与违约之间的非线性关系；多元判别分析要求财务指标变量在组内服从多元正态分布，破产组和非破产组具有相同的协方差矩阵，通常与现实情况不符。

2．Logit模型

20世纪70年代以来，研究者开始运用回归分析法测算企业的违约概率。Logit模型是基于Logistic回归建立的企业财务预警模型，由奥尔森(Ohlson)在1980年最先应用。该模型将企业是否发生财务危机(违约)设为一个二值虚拟变量，企业违约记为Y＝1，不发生违约记为Y＝0。假设违约事件发生的概率服从累积Logistic分布，其分布函数可以表达为:

其中，P是企业的违约概率，X是企业的财务指标向量，B为回归系数向量。在此函数中，P与X和B之间是非线性关系，对该等式变形后，可转换成线性函数:

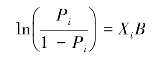
Logit模型不要求自变量符合正态分布，在财务指标不满足正态分布假设的情况下，其预测准确率高于判别分析法；可以反映违约事件概率与解释变量之间的非线性关系；从模型可以直接得出企业的违约概率，因而成为主流的财务预警模型之一。

(三)现代信用风险度量模型

20世纪90年代以来，欧美国家推出KMV模型、信用度量模型、宏观模拟模型、信用风险附加模型等新型信用风险度量模型，其建模思想和基于财务指标的判别分析和回归分析迥然相异。

1．KMV模型

KMV模型是由美国KMV公司在1993年开发的信用风险度量模型。KMV公司根据默顿(Merton)在1974年提出的“资产价值理论”，将债权看作债权人向借款公司股东出售的对企业价值的看跌期权(卖权)，期权标的是公司资产，执行价格是企业的债务价值。企业所有者相当于购买了一项违约或不违约的选择权，在债务到期时，如果借款企业资产的市场价值超出企业的负债，企业有动力偿还债务；如果企业资产的市场价值低于其负债水平，企业的所有者将选择违约，将资产转交给债权人处置。

图14-1中，B点表示债务价值。如果债务到期时企业资产价值下降到其债务价值以下，企业将对其债务违约，而债权人就会遭受损失，最为极端的情况是本息尽失。如果资产价值高于债务价值，则债权人可获得固定的本息。由此图可看出，债权人的收益分布曲线类似看跌期权卖方的盈亏分布曲线。基于该原理，KMV模型预测的是看跌期权可能被执行的概率，也即借款企业的违约概率，取决于债务到期时企业价值低于债务价值的可能性。

由于企业资产的市场价值难以直接观测，KMV公司采用期权定价的原理推算借款企业资产价值及其波动性。企业股东持有的股权可看作是对企业资产价值的看涨期权^[4]，根据期权定价理论，股权价值的公式是:

E＝f(A，σA，B，r，τ)

图14-1　债权人的收益分布

E是股权的市场价值(即看涨期权的价值)，A是公司资产市场价值，σA是资产价值波动性，B是负债价值，r是无风险借贷利率，τ是时间范围。

根据伊藤引理，企业股权价值波动性σE与企业资产价值波动性σA之间存在理论上的关系:

σE＝g(σA)

在上面两个公式中，已知变量有:E，可直接观察得到；σE，可由历史数据估算出；B，公司的违约实施点或违约触发点，为已知常数；τ，一般设定为1年；r，可直接观察得到。公司资产价值A及其波动性σA是未知数。将两个等式联立，可求出这两个未知数。

计算出A和σA的值之后，就可以据此计算企业的违约距离。假定公司未来资产价值围绕其现值呈正态分布，均值为A，标准差为σA，可利用下面的公式计算公司在1年内或t＝0时(现在)距违约触发点的距离，其公式为:

KMV公司基于其拥有的企业数据库，利用历史经验数据估算企业的预期违约频率(expected default frequency，简称EDF)的经验值。假设违约距离为2σA，则经验EDF的计算公式为:

针对单个企业的KMV模型可以扩展到组合模型(portfoliomanager模型)。使用多因素股票收益模型，估算两家企业资产价值变化的相关性，据此推算其违约相关性；计算两家企业的资产价值同时下降到各自的违约触发点以下的概率，即得到两家企业的联合违约频率。进而，估算贷款组合的预期损失和非预期损失。

KMV模型的优点在于:一是基于现代公司金融和期权理论的结构化模型，拥有强有力的理论支撑；二是动态模型，基于对企业股票价格变化的分析估算EDF，对违约概率的预测更具有前瞻性，被视为“向前看”的方法。KMV模型在实际应用中也存在局限性:不能直接运用于非上市企业，需要借助一些会计信息或其他能够反映企业特征的指标来替代模型中的一些重要变量，并通过对比分析得出企业的EDF；对于发展中国家新兴股票市场的适用性需要验证。

2．信用度量模型

信用度量模型(creditmetrics model)由JP摩根银行于1997年推出，旨在估算贷款信用风险的VaR值。

(1)VaR方法的基本原理^[5]

VaR(value-at-risk)即“风险价值”，亦称在险价值，是指在未来给定时期内和给定的置信度下，资产可能发生的最大损失。1993年，JP摩根发布度量市场风险的VaR方法，其后被应用于信用风险度量。例如，JP摩根在1994年年报中公布其日交易VaR值在时间间隔为1天和95%的置信度下，平均约为1 500万美元。其含义是，1994年某一特定时点上的证券组合在未来的1天内，由于市场价格波动而带来的损失不会超过1 500万美元，JP摩根对此有95%的把握，损失大于1 500万美元的概率为5%。VaR可以用数学公式表达为:

Prob(ΔW＞VaR)＝1－a

其中，ΔW为资产在给定的时期Δt内的损失，α为置信度。由上式可知，VaR就是对应于置信度α的资产损益分布的下分位数。

要估算VaR，首先需要选择两个重要参数:一是观察期间，即计算VaR的时间范围。银行通常以每日间隔公布其交易账户的市场风险的VaR，是由于投资组合规模的快速变动。监管者则会考虑监督成本和尽早发觉潜在问题的收益之间的替代关系。二是置信度，其设定并无可遵循的统一规则，若侧重于考虑VaR的有效性(估计精度)，需要选择较低的置信水平，而测算风险资本需求则需要选择较高的置信水平。巴塞尔委员会选择了99%的置信度，这一置信水平反映了监管者对确保金融体系安全有效和最低资本要求对银行的盈利产生不利影响之间的权衡。置信度越高，意味着VaR越大。

估算VaR的关键环节是估计资产收益率或资产价值变化的概率分布，据此计算出VaR值。假定W0为资产的初始价值，R是观察期内的投资回报率。在观察期末，资产价值为W＝W0(1＋R)。回报率R的均值和标准差分别为μ和σ。在给定的置信度α下，资产的最低价值为W*＝W0(1＋R*)，进而计算相对于资产价值均值的VaR，即“相对VaR”:(www.xing528.com)

VaRR＝E(W)－W*＝－W0(R*－μ)

若为简化VaR的计算，也可以采用参数法，假设资产收益率或资产价值服从正态分布，但这一假设可能和现实不符合，基于正态分布假设估算VaR易于低估风险。

VaR方法的主要优点是:输出的是一个明确直观的风险值，简单易懂，有助于揭示银行的风险承担水平；提供了统一的风险值测度的框架，为全面风险管理提供了工具；可用于预估金融资产组合的最大损失。

VaR方法也存在缺陷:其一，利用历史数据度量信用风险，属于“向后看”(backward-looking)的风险度量方法；其二，忽略了极端负面冲击的尾部风险。2007年，在经历持续的经济繁荣期之后，美国次贷危机爆发，银行业遭受了超出预期的更为频繁和严重的损失，VaR方法由于对风险评估不充分而受到质疑，银行应结合压力测试等手段对其进行补充。

(2)单项贷款的VaR测算

测算单项贷款的VaR值的具体步骤如下:

①估算债务人的信用等级迁移概率。在观察期末，债务人由期初的初始信用等级迁移到其他信用等级或维持原等级的概率即为等级迁移概率。假定实际信用等级迁移概率等于历史平均迁移概率，可以利用历史数据得到信用等级迁移概率。

②估算未来不同信用等级下的贷款远期价值。贷款的理论市场价值随信用等级变化而变化。若信用等级下降，信用风险溢价(信用价差)随之增大，贷款价值(未来各期现金流折现值之和)下降。若信用升级，则信用价差变小，贷款价值上升。贷款的估值公式如下:

R为各期固定利息，F是贷款金额，n是贷款剩余期限，r为无风险利率，s为信用价差。

③得出贷款远期价值的概率分布。将不同等级的期末贷款价值与迁移概率结合，即得到贷款价值在期末的实际分布。

④计算贷款远期价值的均值和标准差，在此基础上求出VaR值。假设贷款价值服从正态分布，置信度为95%下的VaR值为1．65×σ，置信度为99%下的VaR值为2．33×σ。若基于贷款价值的实际分布，贷款的VaR值的计算公式为:

贷款VaR值＝贷款均值－与给定的置信度对应的贷款远期价值

例　假设一项5年期的固定利率贷款，年利率为6%，金额为1亿元。借款企业的信用等级为BBB。给定观察期为1年。借款企业在下一个年度可能向8种信用级别迁移，包括升级、降级和评级不变。见表14-1。

表14-1　贷款信用风险的VaR计算

资料来源:CreditMetriesTM-Technical Document．J．P．Morgan．Apri1 2，1997:10．

第1年末贷款价值的均值μ＝10 709万元，标准差σ＝299万元。假定贷款价值服从正态分布:

在95%置信度下，VaR＝1．65×σ＝493(万元)

在99%置信度下，VaR＝2．33×σ＝697(万元)

基于正态分布假设会低估实际的VaR值，根据贷款价值的实际分布:

在95%置信度下，VaR＝10 709－10 202＝507(万元)

在99%置信度下，VaR＝10 709－9 810＝899(万元)

(3)贷款组合的VaR测算

JP摩根将单项资产模型加以延展，使之成为组合风险计量模型。为便于理解，假设组合由两笔贷款构成，估算组合VaR值的具体步骤如下:

①得出两笔贷款的联合信用等级迁移概率矩阵。首先，将借款企业资产价值的波动性与借款人信用等级变化相联系。假定企业资产价值变化幅度达到一定程度时其信用等级就会改变，由此得到等级迁移与企业资产价值变化之间的映射关系。其后，计算两企业资产价值的相关系数。然后，将相关系数代入两企业资产价值的联合正态分布密度函数中，计算两资产价值波动范围分别在一定区域内的联合概率，该概率即等于和资产价值变动区域相对应的两企业未来信用等级状态的联合迁移概率。两贷款组合应得到一个8×8的联合迁移概率矩阵。

两家企业的联合信用等级迁移概率为:

其中，Xi和Xj代表任意两个信用等级，对于有8个级别的评级系统，i，j∈(1，2，…，8)。Y1和Y2分别表示两家企业的资产价值，(a，b)和(c，d)分别表示和两个信用等级对应的企业资产价值波动范围，f(·)是两企业资产价值的联合正态分布密度函数，ρ是两企业资产价值的相关系数。

②求出在不同信用等级状态下贷款组合的市场价值。计算单笔贷款在未来每种信用等级状态下的价值，再将组合中每笔贷款的价值加总，即得到组合的价值。最终得到一个8×8贷款组合价值矩阵。

③得出贷款组合价值的概率分布。已知贷款组合在不同信用等级状态下的价值及相应的联合转移概率，可得到组合价值的实际分布。

④求出贷款组合价值的均值与方差，进而计算贷款组合基于实际分布或正态分布的VaR值。

3．宏观模拟模型

Creditmetrics模型假定等级迁移概率在经济周期不同阶段之间是稳定的，然而等级转移对经济周期是比较敏感的。为修正这个偏差，麦肯锡公司提出宏观模拟模型(loan portfolio view，又称信贷组合观点)，试图将宏观因素与迁移概率的关系模型化，求解基于宏观条件的迁移概率模拟值，以有条件迁移矩阵取代基于历史数据的无条件迁移矩阵，以便求出对经济周期敏感的VaR值。

宏观因素与转移概率间的关系可用函数式描述:

Pt＝f(yt)

Pt表示时间t上未来1年内借款人从C级移往D级的概率(PCD)，yt表示时间t上的一整套宏观因素所构成的经济状态。yt由系统宏观因素和非系统宏观因素驱动，前者包括GDP增长率、失业率等，后者指经济体系受到的随机冲击或创新。系统宏观因素受其历史值影响，也对当期受到的冲击敏感。

由于历史值已知，冲击因素可以用蒙特卡罗方法模拟得到，最终，可求出Pt的模拟值，可模拟出未来多期(t，t＋1，…，t＋n)的PCD的情景值。

按上述思路，同样可以对转移矩阵中所有的其他元素进行调整，估算出以宏观经济状态为条件的未来各期t，t＋1，…，t＋n的转移概率模拟值，进而得到未来各期的有条件的模拟转移矩阵，从而取代以历史数据为基础的无条件的转移矩阵，并计算出对经济周期敏感的未来各期的VAR值。该模型也可以计算周期影响下的违约损失率。

4．信用风险附加模型

瑞士信贷银行开发的信用风险附加模型(Creditrisk＋)借鉴了财产火险精算理论。每处房屋遭遇火灾是独立的小概率事件，同样可假定大规模信贷组合中每笔贷款的违约概率较小且违约事件相互独立，因此组合中发生违约事件的次数近似于泊松分布。房屋失火的损毁程度可能差别很大，贷款的违约损失程度同样很不确定，由于逐笔度量损失程度较困难，可按贷款风险暴露将信贷组合划分为若干频段(次级组合)，以降低不精确性。将不同频段的损失分布加总，可得到贷款组合的损失分布。

模型的具体步骤如下:

①将贷款组合按单笔贷款的风险暴露划分为若干频段。

②求出各频段的违约概率分布。首先，根据历史数据确定某频段的平均违约率。其次，将平均违约率代入泊松分布函数中，可求得频段中违约次数的概率。最后，将违约次数和相应的概率结合，可得到该频段违约次数的概率分布曲线。

③计算各频段的损失分布。将违约损失值与对应的违约概率结合，可得到该频段的损失分布曲线。

④将各频段的损失分布加总得到组合损失分布。进而，计算出未预期到的损失值，即可确定组合的经济资本要求。