让罗马大败的秘密武器
阿基米德将自己锁在一间小屋里,正夜以继日地埋头写作《浮体论》。这天突然闯进一个人来,一进门就连忙喊道:“哎呀!你老先生原来躲在这里。国王正调动大批人马,在全城四处找你呢。”阿基米德认出他是朝廷大臣,心想,外面一定出了大事。他立即收拾起羊皮书稿,伸手抓过一顶圆壳小帽,随大臣一同出去,直奔王宫。
当他们来到宫殿前阶下时,就看见各种马车停了一片,卫兵们银枪铁盔站立两行,殿内文武满座,鸦雀无声,国王正焦急地在地毯上来回踱步。由于殿内阴暗,天还没黑就燃起了高高的烛台。灯下长条案上摆着海防图、陆防图。阿基米德看着这一切,就知道他最担心的战争终于爆发了。
公元前216年,眼看迦太基人将要打败罗马人,国王很快就和罗马人决裂了,与迦太基人结成了同盟,罗马人对此举很恼火。现在罗马人又打了胜仗,于是采取了报复的行动,从海陆两路向这个城邦小国攻过来,国王吓得没了主意。当他看到阿基米德从外面进来,连忙迎上前去,恨不得立即向他下跪,说道:“啊,亲爱的阿基米德,你是一个聪明的人,先王在世时说过你都能撬动地球。”
关于阿基米德撬动地球的说法,却还是他在亚历山大里亚留学时候的事。当时他从埃及农民提水用的吊杆和奴隶们撬石头用的撬棍受到启发,发现可以借助一种杠杆来达到省力的目的,而且发现,手握的地方到支点的这一段距离越长,就越省力气。由此他提出了杠杆原理。为此,他曾给当时的国王亥尼洛写信说:“我不费吹灰之力,就可以随便移动任何重量的东西;只要给我一个支点,给我一根足够长的杠杆,我连地球都可以撬动。”可现在这个小国王并不懂得什么叫科学,他只知道在大难临头的时候,借助阿基米德的神力来救他的驾。
阿基米德虽然对因国王目光短浅造成的这场祸灾非常不满,但木已成舟,国家为重,他扫了一眼沉闷的大殿,捻着银白的胡须说:“如果单靠军事实力,我们绝不是罗马人的对手。现在若能造出一种新式武器来,或许还可守住城池,以待援兵。”
两天以后,天刚拂晓,罗马统帅马赛拉斯指挥着他那严密整齐的方阵向护城河攻来。今天方阵两边还预备了铁甲骑兵,方阵内强壮的士兵肩扛着云梯。马赛拉斯在出发前曾口出狂言:“攻破叙拉古,到城里吃午饭去。”在喊杀声中,方阵慢慢向前蠕动。照常规,城头上早该放箭了。可今天城墙上却是静悄悄地不见一人。也许是几天来的恶战使叙拉古人筋疲力尽了吧,罗马人正在疑惑,城里隐约传来吱吱呀呀的响声,接着城头上就飞出大大小小的石块,开始时大小如碗如拳一般,以后越来越大,简直有如锅盆,山洪般地倾泻下来。石头落在敌人阵中,士兵们连忙举盾护体,谁知石头又重,速度又急,一下子连盾带人都砸成一团肉泥。罗马人渐渐支持不住了,连滚带爬地逃命。
阿基米德到底造出了什么秘密武器让罗马人大败而归?原来他制造了一些特大的弩弓——发石机(见图5.2.1)。这么大的弓,人是根本拉不动的,他就利用了杠杆原理。只要将弩上转轴的摇柄用力扳动,那与摇柄相连的牛筋又拉紧许多根牛筋组成的粗弓弦,拉到最紧时,再突然一放,弓弦就带动载石装置,把石头高高地抛出城外,可落在很远的地方。原来这杠杆原理并不是简单使用一根直棍撬东西。
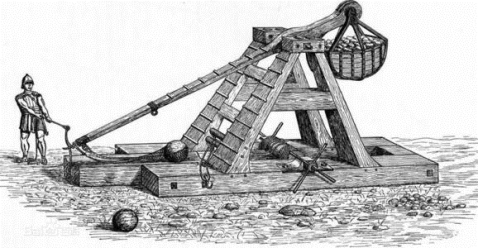
图5.2.1 发石机
在今天,人们对杠杆原理的应用还有哪些呢?打开本节的内容,去了解吧!
表5.2.1 分层学习要求
如图5.2.2所示,木板上钉了一只图钉,你会选用下图中的哪种工具把图钉从木板中拔出来呢?

图5.2.2 形形色色的工具
杠杆及五要素
杠杆是简单机械中的一种,图5.2.3所示都是生活中常见的杠杆。
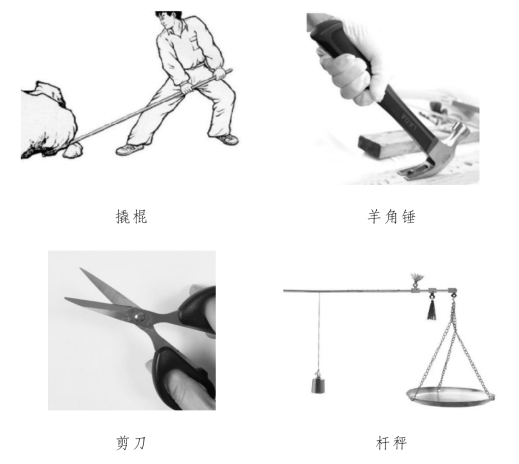
图5.2.3 生活中的杠杆
1.杠杆一定是一根木棒吗?
对于形态各异的杠杆,是否具有共同的特点呢?
使用撬棒时,撬棒可以绕着小石头的顶点转动;使用羊角锤时,它会绕着锤头的另一端点转动;使用剪刀时,刀口绕着连接点转动。我们将在力的作用下能够绕着固定点转动的坚实物体称为杠杆。
影响杠杆使用效果的因素有以下五点:
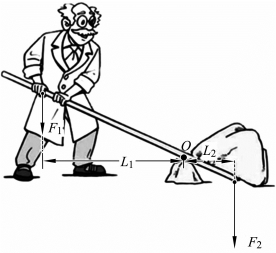
图5.2.4 杠杆的五要素
2.动力和阻力的作用点在哪?
3.杠杆的支点和力臂一定在杠杆上吗?
如图5.2.4所示,杠杆绕某固定点转动的点称为支点;使杠杆转动的力称为动力可用符号F1表示;阻碍杠杆转动的力称为阻力可用F2表示;从支点O到动力F1作用线的距离L1称为动力臂;从支点O到阻力F2作用线的距离L2称为阻力臂。
杠杆平衡条件
两位同学玩跷跷板,这也是生活中常见的杠杆。当跷跷板两端的同学在空中保持静止或匀速上下转动时,我们称此时杠杆处于平衡状态,即此时的动力作用转动效果和阻力的作用转动效果相互抵消。
如图5.2.5所示,此时两小朋友在空中静止,若换一个大人坐在右端,那么跷跷板会立马向右端倾斜,不再是平衡状态。若要再次使跷跷板恢复平衡状态,大人应该向哪个方向移动呢?

图5.2.5 跷跷板
4.什么是杠杆的平衡状态?
这个示例表明:杠杆的平衡不仅与力有关,还与支点到力作用线的距离有关。
实验探究
杠杆平衡条件
实验器材:杠杆、支架、50 g钩码若干、刻度尺、细线。
(1)如图5.2.6所示,将杠杆中点支在支架上,调节杠杆两端的平衡螺母使杠杆在水平位置平衡。
图5.2.6 天平第一次调平衡
(2)如图5.2.7,在左右两端挂上不同数量的钩码,移动钩码的位置,使杠杆恢复至原来平衡位置。
图5.2.7 天平第二次调平衡
5.为什么将杠杆调至水平位置平衡?
(3)记录钩码的个数,测量钩码到支点的距离并记录到表5.2.2中。
(4)更换钩码个数,重复以上实验步骤。
6.此实验中,多次测量的目的是什么?
表5.2.2 天平平衡实验数据

从实验中我们可以知道,杠杆平衡的条件是
![]()
或写成
![]()
如图5.2.8所示,我们也可以用弹簧测力计拉杠杆进行探究杠杆平衡的条件。甲乙两种方使杠杆平衡,其示数1F和1F′的大小关系?倾角变大,弹簧测力的示数怎么变化?
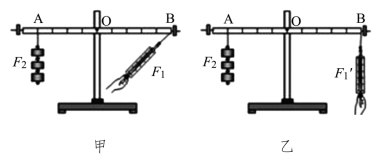
图5.2.8 力沿两个方向施加
7.当L1=L2时,你有什么发现?
8.弹簧测力计斜拉杠杆时,为什么倾角越大,示数越大?
可以发现,垂直杠杆向下拉的时候,等式![]() 依然成立。一旦倾斜,示数随之改变,因为1F′的力臂发生了改变。式子
依然成立。一旦倾斜,示数随之改变,因为1F′的力臂发生了改变。式子![]() 仍然成立。并且还发现:倾斜角度越大,示数也越大。
仍然成立。并且还发现:倾斜角度越大,示数也越大。
在物理学上,我们把力与其力臂的乘积称为力矩,用M表示,单位是N·m。因此杠杆平衡条件也可以写作
9.请思考,如何确定最小力?
![]()
式中,M顺表示能使杠杆顺时针转动的力矩,M逆表示使杠杆逆时针转动的力矩。因此,杠杆平衡条件又称之为力矩平衡条件。
杠杆的分类
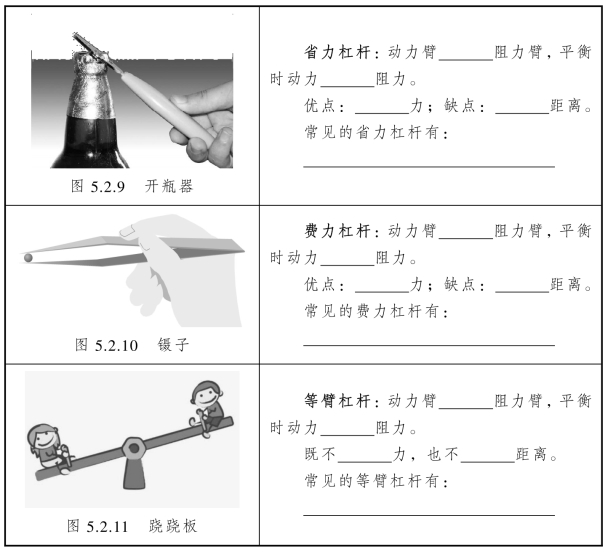
生活中有许多杠杆给我们带来了不同的便利。例如:图5.2.9开瓶器、5.2.10镊子、5.2.11小朋友玩的跷跷板……根据动力臂与阻力臂的长短比较,杠杆可以分为省力杠杆,费力杠杆和等臂杠杆。
请作出以下杠杆的力臂,并完成表5.2.3中的填空。
表5.2.3 杠杆的分类
例题1:如图5.2.12所示,甲、乙两同学用一根轻质木棒抬重物,若甲乙两同学肩膀间的距离d=1.6 m,物体到甲同学肩膀处的距离为L=1.0 m,木棒对乙同学的压力大小为300 N,求:
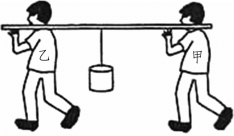
图5.2.12 两同学用木棒抬水
(1)物体重力多少?
(2)木棒对甲同学肩膀的压力是多大?
分析:(1)以木棒和甲同学的接触点为支点,由杠杆平衡条件F乙d=FL,求解绳子对杠杆的拉力F,即得物体的重力G。
(2)以木棒和乙同学的接触点为支点,由杠杆平衡条件F甲d=F(d-L),求解甲同学肩膀对木棒的支持力F甲。
解:(1)以木棒和甲同学的接触点为支点,杠杆受绳子拉力F和乙同学肩膀对木棒的支持力F乙而处于杠杆平衡状态,如图5.2.13甲所示。
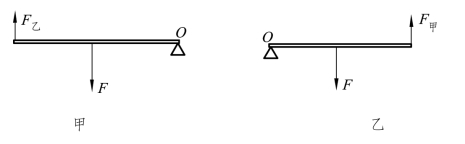
图5.2.13 受力分析
由杠杆平衡条件 F乙d=FL
解得绳子的拉力

则物体的重力G=F=480 N。
(2)以木棒和乙同学的接触点为支点,杠杆受绳子拉力F和甲同学肩膀对木棒的支持力F甲而处于杠杆平衡状态,如图5.2.13乙所示,由杠杆平衡条件
![]()
解得
![]()
有没有注意到F甲+F乙=F?是偶然还是必然?
实际这正是物体受力平衡的体现!(https://www.xing528.com)
如图5.2.14所示,轻质细杆受到竖直向下的绳子拉力F,甲同学肩膀对木棒的支持力F甲和乙同学肩膀对木棒的支持力F乙而处于平衡态,根据二力平衡原理有
![]()
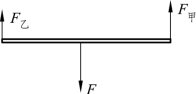
图5.2.14 受力分析
由此可见,一般情况下,受力作用的物体,平衡的条件为

例题2:小杰同学发现了一个金属块,他想知道它的重力和密度。他手中只有一只量程较小的弹簧秤,当他用此弹簧秤测量此金属块的重力时,发现已超过弹簧秤的最大量程,于是他设计了如图5.2.15乙所示的装置去测量,轻质细杆的质量忽略不计。图中OA∶OB=3∶1,用细绳把金属块悬挂于B点,用弹簧秤在A点施加一个竖直向上的力,当杠杆水平静止时,弹簧秤读数为18 N;当向容器中加水,金属块浸没水中后,弹簧秤读数为12 N。g取10 N/kg。求:
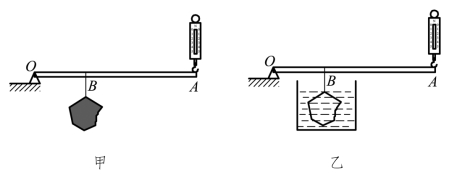
图5.2.15 示意图
(1)属块的重力为多少?
(2)金属块浸没于水中后所受到的浮力为多大?
(3)金属块的密度是多少?
分析:(1)未浸入水时,杠杆在拉力和金属块的重力作用下处于杠杆平衡状态,则由杠杆的平衡条件可求得金属块的重力。
(2)当金属块浸入水中时,由杠杆的平衡条件可求得绳对B点的拉力,而绳对金属块的拉力与金属块对绳的拉力为相互作用力,故可知金属块所受拉力,则由力的合成可求得浮力。
(3)由浮力公式可求得金属块排开水的体积,即可得金属块的体积,由重力公式可求得金属块的质量,则由密度公式可求得金属块的密度。
解:(1)杠杆在弹簧秤的拉力F1及细绳对B的拉力T1作用下而处于平衡状态,如图5.2.16甲所示。
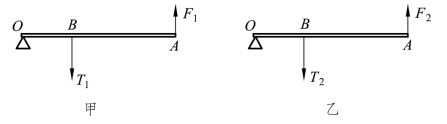
图5.2.16 受力分析
由杠杆平衡条件可得
![]()
得
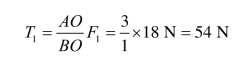
金属块受到绳子的拉力![]() 。
。
金属块受到绳子对它的拉力T1′和地球对它的重力G而平衡,故
![]()
(2)杠杆在弹簧秤的拉力F2及金属块对B的拉力T2作用下而处于平衡状态,如图5.2.16乙所示,则由杠杆的平衡条件可得:
![]()
解得![]()
金属块受到绳子的拉力![]()
金属块受到绳子对它的拉力T2′,水对它的浮力F浮,地球对它的重力G而平衡,故
![]()
解得![]() 。
。
(3)由浮力公式![]() 可求得金属块排开水的体积,即金属块的体积
可求得金属块排开水的体积,即金属块的体积

金属块的密度
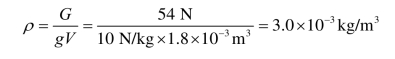
自我评价
1.爱劳动的小明春节去给外婆家拜年时,想和爸爸一起去果园修理果枝,他在家里的工具箱里翻出了下面几种剪刀(如图所示),应当选择哪一种最为合适( )。

2.如图5.2.17所示为等刻度轻质杠杆,A处挂2牛的物体,若使杠杆在水平位置平衡,则在B处施加的力( )。

图5.2.17
A.可能为0.5牛 B.一定为1牛 C.一定为4牛 D.可能为2牛
3.如图5.2.18是一个指甲刀的示意图,它由三个杠杆ABC、OBD和OED组成,用指甲刀剪指甲时,其中,ABC是________杠杆;OED是________杠杆。(填“省力”“费力”或“等臂”)
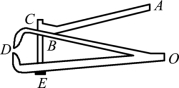
图5.2.18
4.如图5.2.19所示,利用羊角锤撬起钉子,请你在羊角锤A点处画出所能施加最小动力F1。
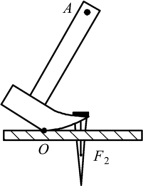
图5.2.19
5.如图5.2.20所示,教室里学生座椅的侧视图,现在小明同学要在C点用最小的力使座椅绕A开始逆时针旋转,请在图上画出这个力F的力臂以及力F的示意图。
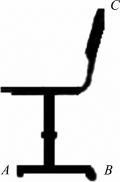
图5.2.20
6.园艺师用绳子将古树系住,通过山体固定,对古树展开救助。如图5.2.21所示,把古树视为杠杆,O点为支点,A点为古树重心位置。请画出:
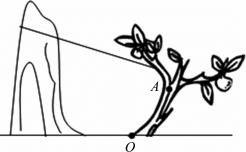
图5.2.21
①古树受到的重力G的示意图;②绳子拉力的力臂L。
7.小华在做“探究杠杆平衡条件”实验时的装置如图5.2.22所示。

图5.2.22
(1)杠杆在图甲所示的位置静止时,杠杆_____(选填“是”或“不是”)处于平衡状态。
(2)将杠杆调节到水平位置平衡后开始实验,杠杆两侧挂上钩码后,发现杠杆倾斜,为使杠杆重新在水平位置平衡,小华采用调节平衡螺母的方法,请判断这种做法是否可取?_____。
(3)如图乙所示,当杠杆在水平位置平衡后,从杠杆的两侧同时减掉一个钩码,那么杠杆的________(选填“右”或“左”)端下沉。
(4)在图丙中,将弹簧测力计由竖直方向旋转至沿虚线方向,如果要继续保持杠杆在水平方向静止,弹簧测力计的示数_____(选填“变大”、“变小”或“不变”)。
(5)若杠杆没有在水平位置平衡时就在杠杆两侧挂上钩码进行实验,则此操作对实验产生的影响说法不正确的是_____。
A.杠杆自身重力可能会对实验产生影响
B.可能不便于测量力臂或力臂测量错误
C.无法得出杠杆平衡条件
古代的杠杆
人们很早就知道利用杠杆来搬运重物。4500年前,古埃及人在建造金字塔时就使用撬棍来推动巨石前进,如图5.2.23所示。
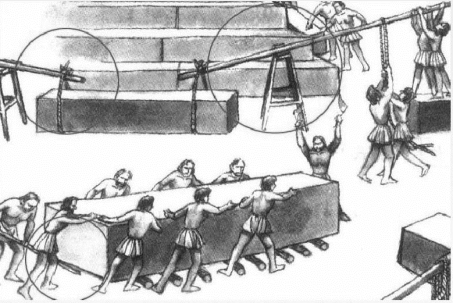
图5.2.23 古埃及人建造金字塔利用杠杆
杠杆在古代中国则有着更加丰富的用途。1981年,在长沙发掘出一套战国时期的天平(见图5.2.24),最小的砝码只有0.6克,在当时是相当精确的称量工具;而另一种称量工具——杆秤(见图5.2.25),距今也有超过2000年的历史,至今仍在使用,其制作工艺也被许多地区作为非物质文化遗产加以保护。

图5.2.24 战国时期的天平

图5.2.25 杆秤
在农业方面的例子更是举不胜举,例如春秋时期鲁、卫、郑等国人民利用“桔槔”来打水(见图5.2.26),魏晋时期发明了用水力驱动的舂米机械“连机碓”(见图5.2.27)。想要知道更多中国古代科技的辉煌成就,大家可以查阅明代宋应星所编纂的《天工开物》,相信你一定会为我们祖先的聪明才智发出由衷地感叹。
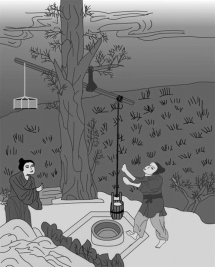
图5.2.26 桔槔

图5.2.27 连机碓模型
人体内的杠杆
人体相当于一部精密的机械,由各种骨骼、关节、肌肉组合而成。我们的每个动作,都需要肌肉收缩来提供动作,使骨骼绕关节转动,因此也相当于一个个的杠杆。漫长的生物进化保证了每个杠杆结构都有其独特的生理功能。
下图所示的是人体内的一些杠杆。如图5.2.28所示,踮脚时,身体重量落在脚掌心,而小腿肌肉在脚跟出提起脚掌,这是个省力杠杆,踮起脚来就不会吃力。如图5.2.29所示,抬手时,肱二头肌在肘关节处拉动小臂,这是个费力杠杆,但可以使手臂摆动的幅度更大一些。
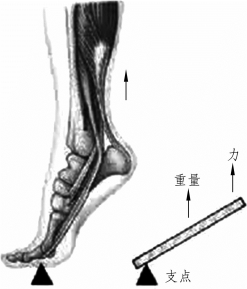
图5.2.28 踮脚
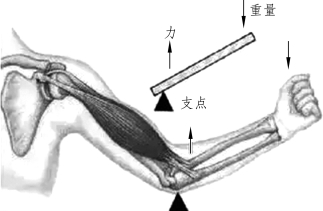
图5.2.29 抬手
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




