大气压强及其现象

格里克与马德堡半球实验

17世纪中期，几乎与意大利和法国同时，关于真空问题的研究也在德国独立地进行，并最终诞生了著名的马德堡半球实验：实验是由格里克（1602—1686）设计的。这位出身于名门望族的德国工程师早年曾游学于荷兰、法国和英国，学习法律和数学。17世纪二三十年代的战争，将他的家乡马德堡变成了废墟。1646年，他当上了该市的市长，在任35年，为重建家乡殚精竭虑。青年时代的他对欧洲学界正关注的真空问题有所了解，而且产生了浓厚的兴趣。他很反感当时盛行的亚里士多德派学者的理论辩护，认为“雄辩术、优雅的语言或争论的技巧，在自然科学的领域中是没有用处的”，他决定用实验来解决这个问题。

一开始，格里克使用一个装满水的葡萄酒桶。用黄铜泵将桶内的水抽出，但桶不太严实，水抽出后，不久即有空气进入。格里克用空心铜球代替木桶继续实验，起初抽起来比较轻松，后来活塞很难拉动了，再后来“啪”的一声巨响，铜球瘪了。格里克又换上更结实的铜球。这一次铜球没有瘪，但抽完气后往里放气的场面十分吓人。格里克改进了抽气机，制造了许多真空球。他发现，在真空中，火焰熄灭了，小动物不能存活，而水果却可以保鲜很长时间。使用他的抽气机，他测量了空气的重量。

1654年，当着德皇斐迪南三世和国会议员们的面，格里克演示了大气压力的威力。他先两个直径约1.2英尺的铜制半球涂上油脂再对接上，然后把球内抽成真空。这时让两个马队分别拉一个半球，直到用上了16匹马才将两个半球拉开。这个著名的实验使真空和大气压力的概念广为世人所熟悉，后人将这两个半球命名为马德堡半球。^[1]

表3.4.1　分层学习要求

大气压强的存在

做一做

如图3.4.1所示，在一个透明杯子中装满水，并在杯口覆盖一张纸片，确保纸片紧贴杯口，然后快速将水杯旋转一定的角度，发现纸片并没有掉下来，为什么会发生这样的现象呢？

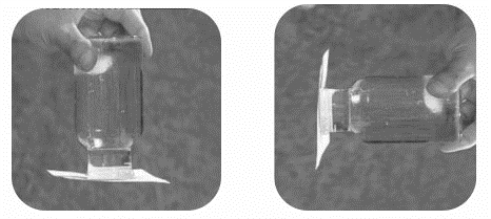
图3.4.1　覆杯实验

1.你能举出生活中的事例来说明大气压是存在的吗？

对纸片进行受力分析：纸片受竖直向下的重力作用，受水向下的压力作用，却没有下落，那么必须受向上的力的作用。这个向上的力的施力物体只能是空气，因此空气也有压强。若将杯子倾斜不同位置，纸片同样不会掉下来，水不会流出来，这说明空气朝各个方向都有压强。

由于空气具有流动性和重力，空气内部向各个方向都有压强，这种压强称为大气压强，简称大气压或气压。

你还能举一些例子来证明大气压强的存在吗？

●瓶“吞”鸡蛋

将一个剥壳的了熟鸡蛋放在一个广口瓶的杯口（杯口略小于鸡蛋），鸡蛋不会掉入杯中。再将一小块点燃的酒精棉放入广口瓶中，并将鸡蛋放在瓶口，静置一段时间，发现鸡蛋被逐渐吸入瓶中。

2.为什么大气也有压强？它和固体、液体的压强有什么不同？

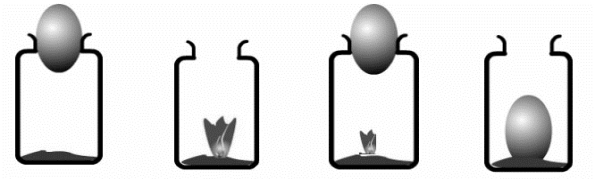
图3.4.2　瓶吞鸡蛋实验

造成这样的现象是因为酒精棉的燃烧消耗了瓶中的氧气，导致瓶中的气体减少，气压减小，内部的气压小于外界的大气压强，从而使鸡蛋被大气压压入瓶中。

●被压扁的瓶子

如图3.4.3所示，将矿泉水瓶中倒入一定量的热水并摇晃，使矿泉水瓶内部空气受热。将水倒出，迅速拧紧瓶盖。再往矿泉水瓶上浇冷水，可以看到矿泉水瓶逐渐被压扁。你能解释其中的原因吗？

图3.4.3　被压扁的瓶子

这是由于矿泉水瓶内的热空气遇冷收缩，瓶内气压减小，低于外界大气压，形成压强差。在大气压的作用下，矿泉水瓶被压扁了。

还有许多与此类似的例子可以证明大气压的存在。如图3.4.4甲所示，把吸盘挂钩往墙上用力一按，吸盘内的空气就会被挤掉，使得吸盘挂钩内的气压比吸盘挂钩外的大气压小，从而在大气压的作用下将吸盘挂钩紧紧地按在墙上。如图3.4.4乙所示，用吸管喝饮料时，在没有吸吮时，吸管内大气压强与杯子内液面受到的大气压强的大小相等；用力吸吮，吸管内的空气被吸走，使得管内的气压低于外界大气压，形成压强差，饮料被大气压挤压进嘴中。注射器吸取药液、打气筒、抽水泵、抽水马桶、钢笔吸墨水都利用了同样的原理。

图3.4.4　生活中的大气压强

想一想

1654年，德国马德堡市格里克和他的助手制造了两个直径为14英寸的铜半球。每个半球上都铸有铜环，其中一个半球上还装有可供抽气的带活塞开关的孔。格里克将两个半球合在一起，用气泵将里面的空气抽出，然后在两个半球上拴了16匹强壮的马向两边拉，如图3.4.5所示，费了很长时间，马用尽了全力才将两个半球拉开。格里克将两个半球取下来，照原样把它们合在一起，再用气泵将里面的空气抽出，这次他没再用马匹来拉，而是打开了半球上的活塞开关，放进空气。随后他轻轻一拉，两个半球就分开了。你能解释这是为什么吗？

图3.4.5　马德堡半球实验纪念邮票

当球内外气压相等时，大气压的作用相互抵消，两个半球合拢后无需用力就会分开。

“马德堡半球实验”让大家看到了空气并不是“什么都没有”，而是有质量的物质，并且能对地面上的所有物体施加很大的压力，形象地证明了大气压强的存在。那么大气压强到底有多大呢？

3.能用液体的压强公式来计算大气压强吗？

大气压强的大小

现在，让我们对覆杯实验中的纸片进行受力分析，你能分析出大气压强带来的压力的大小吗？

想一想

“覆杯实验”中，纸片在大气压的作用下被托起，如果我们增大杯子的高度（容量），使杯中的水的质量越来越大，纸片受到的水的压力也越来越大（见图3.4.6），大气压仍能托起纸片吗？

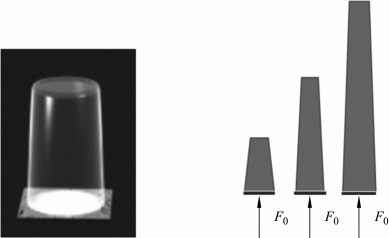
图3.4.6　大气压强带来的压力有多大呢？

临界状态

当物体由一种物理状态变为另一种物理状态时，可能存在一个过渡的转折点，这时物体所处的状态通常称为临界状态，也可理解为“恰好出现”或“恰好不出现”某种现象的状态。与之相关的物理条件则称为临界条件。

我们可以以纸片为研究对象，对大气压强恰好“拖不住”纸片时纸片的受力进行分析：纸片的重力忽略不计，当恰好下落时，水柱对纸片的压力F1和大气对纸片的支持力F0是二力平衡关系（见图3.4.7），即F1=F0

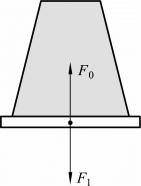
图3.4.7　纸片的受力分析

由

又因为

可解得大气压强的大小为

4.为什么不用水来测量大气压的值呢？

●托里拆利实验

1643年，意大利科学家托里拆利利用“大气压强与液体压强相平衡”的方法，测出了大气压强的数值。如图3.4.9所示，在长约1 m且一端开口的玻璃管内灌满水银，将开口一端堵住，并迅速倒插入盛有水银的玻璃槽内。松开口，管内的水银柱会逐渐下降，但下降到一定高度后不再下降，测得此时管内外水银柱高度差为760 mm。这就是大气压能过托起的水银柱的最大高度。

图3.4.8　托里拆利

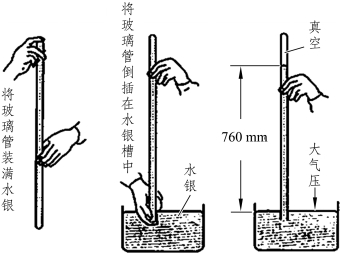
图3.4.9　托里拆利实验

想一想

（1）如果把管子变粗或变细，管内外水银的高度差是否发生改变？

（2）如果把管子倾斜、向上提、向下压，管内外水银的高度差是否发生改变？

（3）如果管内混入了少量的空气，管内外水银的高度差是否会发生改变？

由帕斯卡定律可知，大气压强通过水银传递到水银的各个地方。现在，取玻璃管与水银槽交界面一个“液片”作为受力对象，如图3.4.10所示，这个“液片”受到玻璃管中水银柱的压力F1和大气压强产生的支持力F0。因为F1和F0的受力面积相等，所以玻璃管内760 mm高水银柱产生的液体压强p水银与大气压强p0相等，大气压强的数值为：

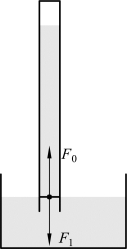
图3.4.10　计算大气压

5.这几种情况测出的大气压的值准确吗？如果不准确，是偏大还是偏小呢？

由以上式子可以看出，大气压强　p0一定，管内外水银面的高度差h不会随着管子粗细的改变、向上提或向下压、管子是否倾斜而改变，始终为一个定值。

如图3.4.11所示，若管内混入了少量的空气，“液片”除了受到玻璃管中水银柱的压力F1和大气压强产生的支持力F0，还受到玻璃管上部的少量空气所产生的压力F2的作用，则玻璃管内水银柱产生的压强值p水银小于水银面上的大气压强值p0，故此时管内外水银的高度差会小于760 mm。

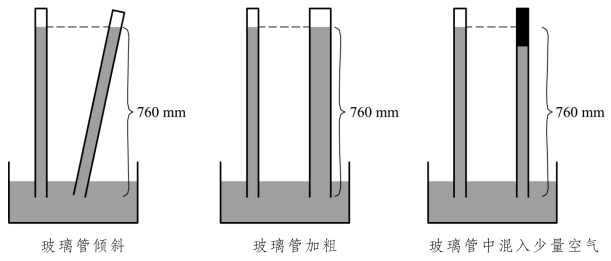
图3.4.11　关于水银柱高度的几种情况

托里拆利真空

在托里拆利实验中，当水银管倒转插入水银槽时，在管内水银上面除了水银蒸气外，并无任何物质，因为水银蒸气的气压极低（在20 °C时只有0.0012 mm水银柱），所以几乎可以看作是真空，这就叫做“托里拆利真空。”

想一想

若将托里拆利实验中的水银换成水，你能否计算出大气压强，能托起多高的水柱呢？你能说明为什么托里拆利实验中不用水吗？

通常我们把760 mmHg或1.013×105Pa叫做标准大气压，用p0表示。在粗略计算时，可以取p0=1×105Pa，这相当于10 N的压力作用在1 cm2上，比大象躺倒时对地面的压强还大。

想一想

（1）你还能想到其他的办法来粗略测量大气压强的大小吗？

（2）如果外界大气压强变了，水银柱的高度是否变化？为什么？

气压计

由可得，若大气压强减小，管内外水银的高度差会减小，反之则增大。故在托里拆利实验中的玻璃管旁立一个刻度尺，读出水银柱的高度就知道当时的大气压了，这就是一个简单的水银气压计，如图3.4.12所示。测量大气压的仪器叫做气压计。

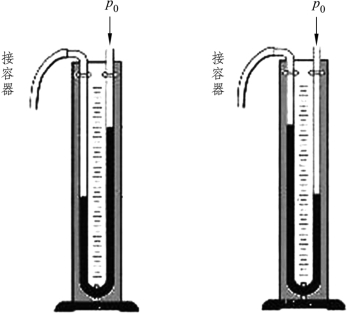
图3.4.12　气压计

转换法

托里拆利实验中，利用大气压强与液体压强相平衡，将看不到的大气压强转换为了看得到的管内外水银的高度差，通过观察管内外水银柱高度差，我们可以判断出大气压强的变化，再次用到了“转换法”。

用一端封闭、一端敞口的U形玻璃管做托里拆利实验，如果在玻璃管旁立一个刻度尺，就可以通过左右两管的高度差得知当时的大气压强相当于多少毫米水银柱的压强。

如图3.4.13所示，水银气压计比较准确，但携带不便，用得比较多的气压计是金属盒气压计，又叫做无液气压计，它的主要部分是一个波纹状真空金属盒。气压变化时，金属盒厚度会发生变化，传动装置将这种变化转变为指针的偏转，指示出气压的大小。氧气瓶和灭火器上的气压计，也是一种无液气压计。

图3.4.13　两种气压计(www.xing528.com)

大气压强的变化

6.影响大气压的因素有哪些？

●大气压强与高度的关系

由于气体也会受到重力的作用，故地表附近的气体密度会比高空的气体密度更大，如图3.4.14所示，海拔越高，气体越稀薄。因此，大气压强会随着海拔的增高而减小。帕斯卡曾测量了不同海拔处大气压强的值，得出了这一结论。

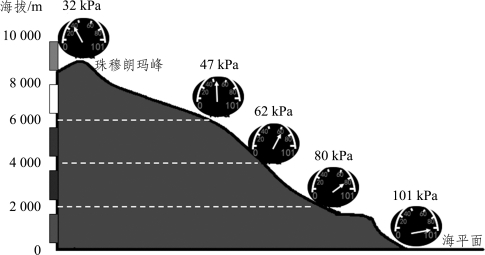
图3.4.14　气压随海拔的变化

在海拔3 000 m之内，每上升10 m大气压强约减小100 Pa。

珠穆朗玛峰上的大气压是海平面的30%左右，空气稀薄、少氧，燃烧困难。2008年为实现奥运火炬在高海拔地区的点火传递，我国科研人员开展了一系列高科技攻关活动。其中火种灯、引火器和火炬的设计经受住了低温、低压和强风等恶劣条件的考验，确保了火炬登顶珠穆朗玛峰的成功。

●大气压强与气象的关系

空气通常都是高气压地区向低气压地区流动。地球表面的空气从高压区向低压区水平流动形成了地面风。

地球表面的地形、地貌不同，即使地表各处的太阳能相同，但各处的温度也存在很大的差异。如图3.4.15所示，如果某地区的地表温度高，地表附近的暖空气上升，则会在地表附近形成低气压，周围地区的空气就在水平方向上向该地区流入，使该地区地表附近包含水蒸气的空气上升，凝结成云形成阴雨天气。

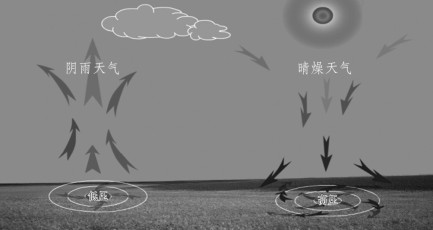
图3.4.15　晴燥天气和阴雨天气

如果某地区的地表温度低，冷空气聚集，在地表附近形成高气压，该地区的空气就在水平方向上向周围地区流出，使该地区上方的空气下降并扩散，带走大量的水分，形成晴燥天气。晴燥天气的气压比阴雨天气的气压高。同理，夏天地表温度高，热空气上升，地表附近气压低；冬天地表温度低，冷空气聚集，地表附近气压高。同样条件下，冬天的气压比夏天高。

由于气压跟天气有密切的关系，所以各地的气压值成为天气预报的依据之一。格里克仿造托里拆利的实验做了一个三层高的水气压计。他通过长期的观察发现水柱高度的变化与天气有关。1660年，他根据一次气压的突然下降，预报了一次大的暴风雨。

●密闭气体压强与温度、体积的关系

如图3.4.16甲所示，试管内被木塞封闭一定质量的气体，用酒精灯均匀加热试管，小木塞一会儿便被弹出。

图3.4.16　探究压强与温度、体积的关系

这说明对于体积一定、质量一定的气体，气体压强与温度有关：温度越高，气体压强越大；温度越低，气体压强越小。

在注射器内密封一部分空气，快速用力挤推活塞压缩气体体积，可以发现气体体积越小，需要越大的力去挤推。由于挤压时间短，温度几乎不变，因此对于质量一定、温度一定的气体，气体压强与体积有关：体积增大，压强减小；体积减小，压强增大。在用打气筒给篮球打气时，向下压打气筒活塞，打气筒内气体的体积减小，压强增大，就有了足够的力将气体从气门进入篮球。而向上拉活塞，体积增大，气压减小，外界空气就被挤入了打气筒。

大气压强的应用

大气压强与我们的生活息息相关。我们可以利用大气压强的作用为生活创造的便利。

●高压锅

水的沸点在标准大气压下是100 °C，随着大气压的减小，水的沸点也会降低。在我国的青藏高原，由于海拔较高，大气压比标准大气压低很多，大部分地区水的沸点仅为84～87 °C。有的哨所海拔5 000多米，水的沸点不足70 °C，这样的温度连面条都煮不熟。为了煮熟东西，则需要增大气压值，提高水的沸点，因此战士们必须使用图3.4.17中的高压锅来做饭。

图3.4.17　高压锅

高压锅把水紧密地封闭起来，使水受热蒸发产生的水蒸气不能扩散到空气中，只能保留在高压锅内，进而使高压锅内部的气压高于1个大气压，也使水的沸点高于100 °C，这样高压锅内部就形成了高温高压的环境，饭很快就熟了。

当然，高压锅内的气压有一定的限制，锅内压力过高时，需通过排气阀排气，以保安全。

●活塞式抽水机

如图3.4.18所示是活塞式抽水机，又叫“汲取式抽水机”，抽水机是一个缸筒，筒内装一个可以上下滑动而且跟简壁紧密配合的活塞，筒底和活塞上各有一个只能向上开的阀门。

图3.4.18　活塞式抽水机

使用时，图3.4.19甲所示，若提起活塞，阀门A受到大气压的作用而关闭，活塞的下面空气稀薄，气压小于外界的大气压。于是，低处的水受到大气压的作用推开阀门B进入圆筒。

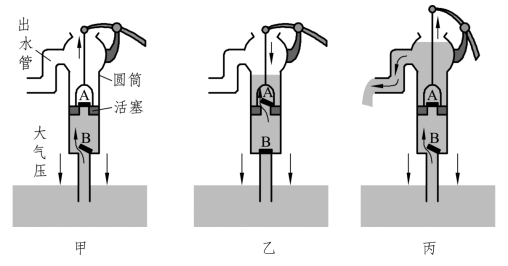
图3.4.19　抽水机的操作过程简化图

当压下活塞时，图3.4.19乙所示，阀门B被水压下而关闭，水被阻不能向下流动，于是冲开阀门A进入圆筒的上部。

再提起活塞时，图3.4.19丙所示，活塞上面的水迫使阀门A关闭，水从侧管流出。与此同时，井里的水又在大气压的作用下推开阀门B而进入圆筒。

这样，活塞不停地上下移动，水就从管口连续不断流出。

想一想

活塞式抽水机能够提升水的最大高度是多少？

这种抽水机的结构简单，操作方便，但出水量小。前面我们知道了一个标准大气压可以托起10.3 m的水柱，故活塞式抽水机提水的高度最多也只能达到10.3 m，通常适用于从深7～8 m甚至更浅的井中抽水。

●离心式抽水机

如图3.4.20甲是一种常用的离心式抽水机（又称为“离心泵”），如图3.4.20乙所示是它的结构示意图（剖面图）。常常用于居民楼生活用水的输送等场景。

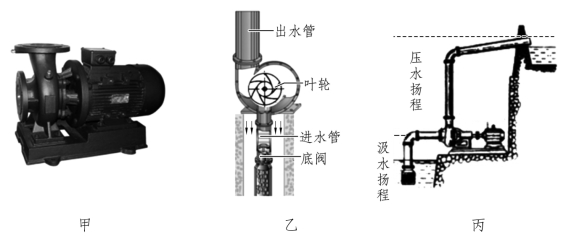
图3.4.20　离心式抽水机及其剖面图

水泵启动前应先往泵里灌满水，启动后，叶轮在电动机的带动下高速旋转，带动泵里的水飞速旋转，水被向外甩出并被压入出水管。水被甩出后，叶轮附近的压强减小，形成比大气压低得多的低压区，外面的水在大气压的作用下，冲开底阀通过进水管进入泵内。冲进来的水在叶轮高速旋转中又被甩出，压入出水管，水就源源不断地从低处被抽到高处。

如图3.4.20丙所示，离心式水泵的抽水高度称为扬程，包括汲水扬程和压水扬程。

第一级扬程称为“汲水扬程”，叶片旋转形成一个低压区，大气压就会把水压入低压区。汲水扬程受限于当地的气压，若当地的气压为1标准大气压，则由于1标准大气压能支持10.1 m高的水柱，所以汲水扬程的极限值是10.1 m。第二级扬程称为“压水扬程”，靠叶片旋转把水甩出去，水甩出去的速度越大，这一级扬程也越大。因此，离心式水泵的抽水高度远远超过了10.1 m。

自我评价

1.下列情景中，没有利用大气压强的是（　）。

A．塑料挂衣钩紧贴光滑的墙壁上

B．钢笔吸墨水

C．用抽气机将马德堡半球中的空气抽出

D．用注射器给病人注射药液

2.用如图3.4.21所示的装置抽水，当活塞上升到S管口后继续上升，则发现的现象有（　）。

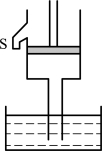
图3.4.21

A．水从S管口流出

B．管内水随活塞继续上升

C．管内水面开始下落

D．水不能从S管口流出，水保持在管口附近不动，既不上升也不下降

3.如图3.4.22所示为盆景的一个自动供水装置。用一个塑料瓶装满水倒放在盆景盘中，瓶口刚刚被水浸没。当盘中的水位下降到使瓶口露出水面时，空气进入瓶中，瓶中就会有水流出，使盘中的水位升高，瓶口又被浸没，瓶中的水不再流出，这样盆景盘中的水位可以保持一定高度。使水不会全部流出而能保留在瓶中的原因是（　）。

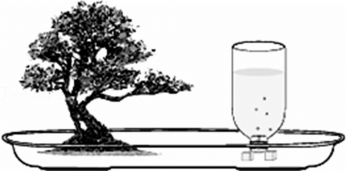
图3.4.22

A．瓶口太小，水不易流出

B．外界大气压强等于瓶内水的压强

C．外界大气压强等于瓶内空气的压强

D．外界大气压强等于瓶内空气的压强与水的压强之和

4.如图3.4.23所示，该装置是某医院内给病人输液的部分装置示意图，乙瓶内液体不断通过Q管输入病人体内，刚开始输液时，甲、乙两瓶内药液量相等，液面相平。过了一会儿，观察两个输液瓶时会发现（此时两个输液瓶内还有大量的溶液）（　）。

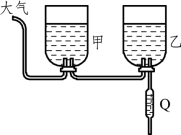
图3.4.23

A．甲瓶中的液面高

B．乙瓶中的液面高

C．甲、乙两瓶中的液面一样高

D．以上三种情况均有可能

5.在测量大气压的实验中，为消除活塞与针筒间的摩擦力对实验的影响，某同学采用了图3.4.24所示的装置，将注射器筒固定在水平桌面上，把活塞推至注射器筒底端，用橡皮帽封住注射器的小孔，活塞通过水平细线与烧杯相连，向烧杯中缓慢加水，当活塞刚开始向左滑动时，测得杯中水的质量为880 g；然后向外缓慢抽水，当活塞刚开始向右滑动时，测得杯中水的质量为460 g，烧杯质量为100 g，活塞面积为7×10-5m2，g=10 N/kg轮轴间的摩擦和细线重不计，则所测大气压的值应为（　）。

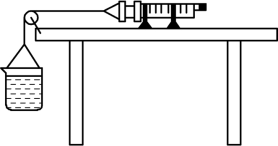
图3.4.24

A．1.26×105Pa　B．1.10×105Pa　C．1.01×105Pa　D．0.96×105Pa

虹吸现象

虹吸是由于液面高度差产生的液体压强与大气压强共同作用产生的一种现象，在我们的生活中多有应用，例如抽水马桶、洗手池回水管等。

虹吸现象的演示装置如图3.4.25所示，将容器A、B装一部分水，并将容器A放在较高的水平台上，将容器B放在水平地面上。现将一根充满水的U形管同时插入两个容器中，可以看见容器A中的水源源不断地通过U形管流入容器B中，直至容器A中的水流尽为止。

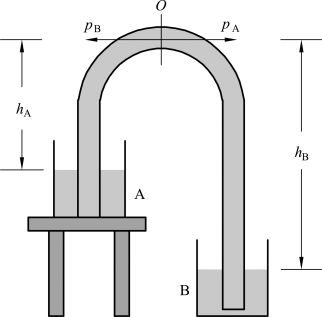
图3.4.25

虹吸现象的原理：在U形管的顶端取一理想的液片O，其左右两侧受到的压强大小分别为pB与pA，令A、B两容器的液面距离液片O的竖直高度分别为hA与hB，设大气压为p0，根据帕斯卡原理与液体压强的计算公式，可以得出：

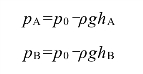
由于hA＜hB，则可以得出pA＞pB，即液片O处的水流方向向右，从而实现将容器A中的水抽入容器B中。