牛顿与万有引力
1665年,一场凶猛异常的瘟疫—— 鼠疫袭击了整个欧洲,夺走了很多人的生命。为了防止瘟疫的蔓延,剑桥大学被迫关闭。当时正在剑桥大学三一学院读书的牛顿,回到了他出生的家乡,在那里居住了两年之久。也就是在这段时间里,牛顿做出了许多伟大的科学发现,抒写了科学史上的一段奇迹。
如图1.4.1所示,传说1666年的一天,牛顿一边在自家花园散步,一边思索科学问题,突然“咚”的一声,一颗苹果落了下来,掉到草地上。牛顿看着这只苹果,思考着:为什么苹果总是竖直落向地面呢?紧接着,他还想到:苹果会落地,而月球却不会掉落到地球上,苹果和月球有什么不同呢?牛顿苦思冥想之后发现,使月球绕着地球转动和使苹果落到地上的力是同一种力。于是提出了对人类具有划时代意义的万有引力定律:自然界中任何两个物体都相互吸引,引力的大小跟这两个物体的质量的乘积成正比,跟它们的距离的平方成反比。

图1.4.1 牛顿与苹果
宇宙间任何两个物体,大到天体,小到灰尘之间,都存在互相吸引的力,这就是万有引力。我们把物体由于地球吸引而受到的力叫做重力。万有引力就是产生重力的原因。但重力不完全等于万有引力。物体要随地球自转,需要有一部分万有引力来提供向心力,如图1.4.2所示。因此,重力是万有引力的一个分力。我们生活的地球上,重力无处不在。没有重力,我们就无法正常站立在地面上,跳起后也无法落回地面,尘土将永远漂浮于空中……整个地球将一片混沌。[6]

图1.4.2 重力与万有引力关系图
表1.4.1 分层学习要求

重力的定义
如图1.4.3所示,蹦极的人、奔流的瀑布,它们最后都会向下掉落,这是为什么?

图1.4.3 生活中的重力现象
1.阅读“课前阅读”,说一说为什么重力的本质是万有引力?重力就是万有引力吗?
蹦极的人,奔流的瀑布,抛出的篮球,它们最后都会向下掉落,是因为它们都受到地球的吸引。由于地球的吸引而使物体受到的力,叫做重力,通常用G表示。地球上及地面附近的一切物体都受到重力。重力的本质是万有引力。
重力的三要素
●重力的大小
我们提着质量不同的物体,感觉轻重不同,如图1.4.4所示,这表明质量不同的物体所受重力不同。那么重力和质量之间满足什么关系呢?

图1.4.4 提物体
实验探究
重力与质量的关系
实验步骤:分别将已知质量的钩码悬挂于弹簧测力计的挂钩上,如图1.4.5所示。待钩码静止时,弹簧测力计示数等于物体所受的重力大小。改变钩码的质量,多测几次。将数据记录在表1.4.2中。

图1.4.5 测量重力与质量的关系
2.使用弹簧测力计前,应注意什么?
3.能否斜着拉弹簧测力计?
4.调零后,能否将弹簧测力计倒置,把钩码挂在测力计拉环上测量?
表1.4.2 记录数据

以重力G为纵坐标,质量m为横坐标,用描点法在图1.4.6中作出重力G随质量m的变化图像。

图1.4.6 描点作图
5.该实验中能否把钩码换成其他物体?
结论:观察图像可以发现,在同一地点物体所受到的重力与其质量的比值是_________,即物体所受的重力跟它的质量成____________。
更多的精确实验表明,物体所受的重力跟它的质量成正比,即
![]()
G表示重力。m表示质量。g叫做重力加速度,为重力与质量的比值,即g=G/m。一般情况下,g=9.8 N/kg,表示质量为l kg的物体所受到的重力为9.8 N。为了简便计算,g可取10 N/kg。
6.你能试着计算出你的重力吗?
g值的大小与地理位置有关。g值随地理位置的变化见表1.4.3。
表1.4.3 g值变化

7.你能从表格中总结出g的大小于哪些因素有关吗?
为什么在电影中,宇航员走路总是看起来轻飘飘的呢?实际上,根据万有引力定律,不同行星对其表面的物体都有引力的作用,类似于“重力”。月球也不例外。但是月球上的g值只有地球的六分之一,宇航员在月球上受到的“重力”小于在地球上受到的重力,所以走路时看起来轻飘飘的。如果完全没有重力,那么人就会飘起来。
但在太空中航行的宇航员是会受到地球吸引的,只是由于在围绕地球高速运动,处于失重状态,看起来就像不受重力似的,漂浮在空中(详见本节“物理之光”)。
●重力的方向
我们先来看一个实验。
实验:重力的方向
1.用透明亚克力水槽装适量蓝色的水。水槽外壁贴上一片画有直角坐标系的玻璃纸,让坐标纸上横坐标与水面完全重合,如图1.4.7所示。

图1.4.7 重力方向实验1
8.你能计算出一位质量为60 kg的宇航员在月球上所受的重力为多少吗?
9.坐标纸的作用是什么?
2.缓慢移近细线悬吊的金属小球。此时看到,悬吊小球的细线与纵坐标线完全重合,这就证明了:重力的方向在竖直方向,如图1.4.8所示。

图1.4.8 重力方向实验2
3.倾斜水槽,待水重新静止后,重复上述步骤,细线与纵坐标线仍然重合。这就进一步证明,重力的方向总是在竖直方向,如图1.4.9所示。

图1.4.9 重力方向实验3
4.再剪断细线,看到金属小球向下掉落,如图1.4.10所示。由此进一步证明:

图1.4.10 重力方向实验4
重力的方向总是竖直向下的。
想一想
如图1.4.11所示,我们站在地面上,脚朝下,站得很稳。但地球是球形的,在我们“脚下”的阿根廷人,好像是脚朝上的,他们为什么也站得很稳呢?

图1.4.11 人站在地球上
如图1.4.12所示,我们生活在地球表面,由于地球近似是个椭球体,对于居住地球上在不同位置的人而言,“竖直向下”的方向一般都不同。“竖直向下”大致为指向地心,偏差并不大。(https://www.xing528.com)

图1.4.12 不同位置的“竖直向下”
10.水的作用是什么?
悬挂重物的细线叫做重垂线(或铅垂线)。如图1.4.13甲所示,由于重力的作用,重垂线总是沿竖直方向。因此可以利用重垂线来确定竖直方向。工人可以用重垂线来检查墙壁是否竖直,如图1.4.13乙所示。还可以用挂有重垂线的T形尺,如图1.4.13丙所示,来检查工作台是否水平。
11.你能说一说T形尺是如何检查工作台是否水平的吗?

图1.4.13 重力方向的应用
12.你还能举一些应用了“重力方向总是竖直向下”的例子吗?
●重力的作用点
重力的作用点叫做重心。实际上,如图1.4.14所示,物体的每一部分都会受到地球的吸引,即重力的作用。但为了研究的简洁方便,我们可以看作物体各部分受到的重力作用集中于一点上,即重心。重心是重力的一个等效作用点。这种研究方法是在保证作用效果相同的条件下,用简单模型、情景对复杂模型、情景进行等效替代,叫做等效替代法。

图1.4.14 物体各部分受到的重力
想一想,要用手指尖水平支撑起一支铅笔,有什么诀窍呢?
形状规则,质量分布均匀的物体重心在其几何中心上。例如,均匀正方形的重心在对角线的交点,均匀细直棒的中心在棒的中点,均匀球体的重心在球心,如图1.4.15所示。

图1.4.15 形状规则,质量分布均匀物体的重心
对于形状不规则、质量不均匀的物体,重心又怎么找呢?如图1.4.16所示,我们可以用悬挂法或支撑法找重心。观察图1.4.16和图1.4.17你能说一说具体方法吗?
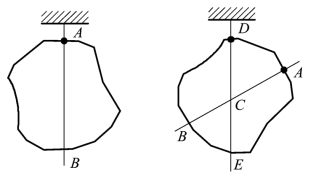
图1.4.16 悬挂法找重心

图1.4.17 支撑法找重心
13.你还能说出哪些质量均匀、形状规则的物体的重心位置呢?
再思考一个问题:物体的重心一定在物体上吗?
如图1.4.18所示,相信能给你提供一点启发。

图1.4.18 物体的重心不一定在物体上
物体的重心是物体所受重力的等效作用点,重心可以不在物体上。
●*理想模型——质点:
我们还可以看作物体的质量也集中于一个等效点,这个点叫做质心。物体受到的重力也集中于该点,因此重心也是质心。在以后的学习中,我们会发现很多时候研究物体的运动和受力时,物体的形状或体积对研究问题几乎没有影响,那么此时为了化简问题,经典力学中往往用一个可以忽略大小和性质的点——重心(或质心)来代表这个物体,这个点又被称作质点(见图1.4.19)。

图1.4.19 质点
重心与稳度
重心的位置对物体的稳定程度有着巨大的影响。如图1.4.20所示,起重机工作时,重心位置不合适,就容易翻倒。高速旋转的轮子,若重心不在车轮转轴上,就会引起剧烈的振动。

图1.4.20 重心对稳度的影响
14.你还能举出哪些通过降低重心或增大接触面提高稳定性的例子?
重心越低,支撑面越大,物体越稳定,即稳度越大。如图1.4.21所示,高脚杯的中心位置比较高,为了提高稳度,高脚杯的支撑面都做得比较大。赛车把车身做得很低来降低重心,轮子也离得比较远来增大支撑面,可以使赛车在快速行驶时不易翻倒。玩滑板时迈开双腿,弯下腰,以增大支撑面,降低重心,来保持身体的平稳。

图1.4.21 提高稳度的例子
想一想
如图1.4.22所示,不倒翁是如何“不倒”的?

图1.4.22 不倒翁
自我评价(第2题选自教科版物理教材八年级下册)
1.由于地球吸引而使物体受到的力叫做重力。那么地球上或地球附近的物体,例如地球上的人、飞在空中的飞机,对地球有力的作用吗?
2.如图1.4.23所示,沿着倾斜的木板往卡车上推油桶。油桶质量是100 kg,用力的示意图把油桶在木板上时所受的重力表示出来。(g=10 N/kg)

图1.4.23
3.试比较质量和重力的异同,并思考:
(1)一个苹果从地球拿到月球上质量和重力是否改变?
(2)一个人能在地球上举起1 000 N的物体,那么他在月球上能举起多少牛的物体?
(3)天平和弹簧测力计在地球上、月球上、太空中能否正常使用?
超重与失重
你听过超重和失重现象吗?人造卫星和宇宙飞船发射过程中有许多超重和失重现象。当人造地球卫星、宇宙飞船、航天飞机等航天器在加速上升阶段,他们对其下方物体的压力是其自身重力的几倍,人和物体就处于超重状态。而当航天器进入轨道后,人和物体又处于完全失重状态,如图1.4.24所示,此时他们对其下方物将没有一点压力。物体在宇宙飞船中完全处于漂浮状态,而这在地球上是很难想象的事情!

图1.4.24 完全失重状态
应当指出,无论物体处于超重还是失重状态,地球作用于物体的重力始终存在,大小也没有发生变化,只是物体对支持物的压力(或对悬挂物的拉力)发生了变化,看起来好像物体的重量有所增大或减小。
那么在地球上可以看到超重或失重现象吗?实际上,我们乘坐游乐园里大摆锤、过山车、跳楼机等项目时,如图1.4.25所示,就会有超重、失重的体验。例如,当跳楼机加速下落时,我们就处于失重状态,会有一种心要从嗓子眼蹦出来的感觉;而减速下落时,我们则处于超重状态。

图1.4.25 体验超重失重的游乐项目
当然,你也可以利用一台电梯和一个体重秤来体验超重和失重。当电梯停止时,你站在体重秤上测出你的体重。启动电梯,当电梯开始上升时,你会发现体重称上的示数变大了。电梯快要到达目的地停止时,体重秤上的示数又变小了。你变得忽“胖”忽“瘦”,这也是超重和失重现象。
【注释】
[1]王仙洲. 中国古代力学的主要成就[J]. 青岛教育学院学报,2001(6):38,40.
[2]徐在新,朱伟. 对四种基本相互作用的认识[J]. 物理教学,1979(4).
[3]向舟书. 艾萨克·牛顿的故事[J]. 初中生学习指导:初二版,2016:91.
[4]徐智鹏. 足球训练中的力学知识分析[J]. 当代体育科技,2018,8,256(34):42,44. 内容有删减和修改
[5]王苗苗,宋雪峰. 伦敦的“达·芬奇”—— 罗伯特·胡克[J]. 少儿科技,2016,000(009):17-18.
[6]逸庐. 课堂上听不到的物理传奇[M]. 杭州:浙江教育出版社,2010.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




