伦敦的“达·芬奇”—胡克
达·芬奇不仅是意大利优秀的艺术家,而且是科学全才,名扬世界。17世纪,英国也有一位伟大的学者,在众多领域贡献卓越,被称为伦敦的“达·芬奇”,他就是罗伯特·胡克(见图1.3.1)。

图1.3.1 罗伯特·胡克
胡克在威斯敏斯特学校学习时,仅用一星期就读完了欧几里得的著作,深受校长赞赏。[5]因此,他在1635年受资助进入大学深造,平时靠合唱团发工资维持生计。胡克在校内认识了许多科学家,不久便成为了著名化学家波义耳的助手。他在没见到任何图纸、只对别人的实验有所耳闻的情况下,做出了充气泵,有助于波义耳提出波义耳定律。英国皇家学会成立后,经波义耳推荐,胡克担任首任实验室主任。在此期间,他发明了多个实验装置。一次,胡克切下一块软木薄片,把它放在自制的显微镜下观察,看到了构成生物体的蜂窝状小室,将之命名为细胞。他是成功观察到细胞的第一人。1665年,胡克出版了《显微镜图》。当时没有照相机,他精心绘制了用显微镜看到的蜜蜂的刺、苍蝇的足等物体的样子。让人们认识到了丰富多彩的微观世界。
胡克对光学问题也进行过系统的研究。他早在1655年就提出光的波动说,认为光的传播与水波的传播相似,后来在1672年进一步指出光波是横波。他还研究过光的干涉现象。把大小不同的重锤连在弹簧上,胡克发现弹簧伸长量和所受拉伸力成正比。他制作了各种材料、形状的弹性体,继续实验,确认了这一结果。1678年,他公布胡克定律。这在现代仍然是重要的力学基本定律。胡克还研究了行星运动,并在1679年写信给牛顿,这启发了牛顿完成万有引力研究。
表1.3.1 分层学习要求
形变
做一做:
1.轻压一把直尺,使它轻微弯曲,撤去压力,直尺会恢复原状吗?
2.把橡皮筋拉长,松手后橡皮筋会恢复至原来的长度吗?
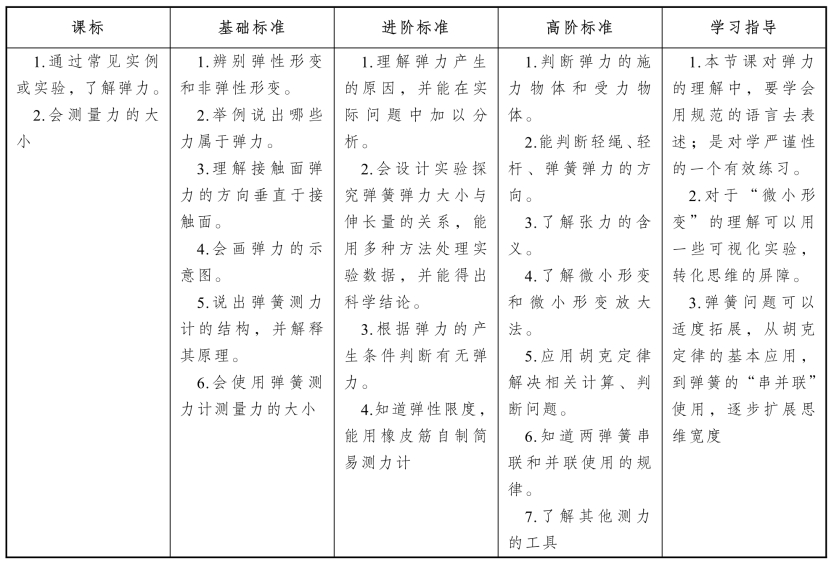
3.如图1.3.2(a)所示,拉一下弹簧,松手后弹簧会恢复至原来的长度吗?
4.如图1.3.2(b)所示,取一块橡皮泥,用手拉,使其变形,手放开,橡皮泥会恢复形状吗?
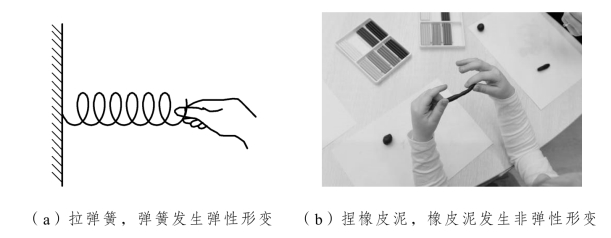
图1.3.2 弹性形变与非弹性形变
5.取一张纸,将纸揉成一团再展开,纸会恢复原来形状吗?
我们可以发现:撤去外力后,直尺、橡皮筋、弹簧均能恢复原状;橡皮泥、纸则不能。如果物体在力的作用下形状或体积发生了改变,就叫做物体发生了形变。形变分为弹性形变和非弹性形变(也叫做范性形变或塑性形变)。
弹性形变:若撤去外力,物体能够恢复原状的形变。例如上述例子中直尺、橡皮筋、弹簧发生的形变。如果形变过大,超过一定限度,撤去外力后,物体不能完全恢复原状,这个限度叫做弹性限度。例如弹簧上的拉力过大时,弹簧就会被拉坏,不能再恢复原状了。
非弹性形变:撤去外力,物体不能恢复原状的形变。例如上述例子中橡皮泥、纸发生的形变。
1.弹性形变和非弹性形变的区别是什么?
想一想
弹簧、橡皮泥的形变都十分明显,可以用肉眼直接观察到。那么用手压桌子,桌子受到手施加的力时,是否发生了形变呢?
在肉眼看来,桌子似乎没有发生形变。我们做一个实验来检验一下吧。
如图1.3.3所示,在桌子上放两面平面镜,由光源发出一束光,这束光经两面镜子之间反射后在墙面上形成一个光点。可以利用刻度尺观察光点的位置。用手按压平面镜中间的桌面。可以观察到墙面上光点的位置发生了变化。这说明,桌面在手施加的力的作用下发生了微小形变。同时,撤去外力后,光点又会回到原来的位置,证明桌面发生的是弹性形变。
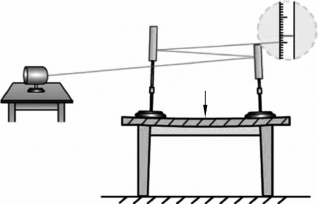
图1.3.3 桌面的形变
2.这里用到了哪种科学研究方法?
与之类似的,还有如图1.3.4所示的装置可以帮助我们观察微小形变。你能说出它的工作原理吗?
![]()
图1.3.4 观察微小形变的装置
当我们用手挤压瓶子时,可以观察到管中的液面上升。这是由于瓶子受到手施加的力,发生了微小形变。
弹力
●定义
发生弹性形变的物体,由于要恢复原来的形状,会对与它接触的物体产生力的作用,这种力叫弹力。
我们常说的压力、支持力、拉力都是由于物体发生弹性形变,要恢复原状时产生的。因此,它们都属于弹力。只不过压力、支持力、拉力是按照力的效果来命名的,叫做效果力。弹力则是按照力的性质来命名的,叫做性质力。
●弹力的作用点
弹力是接触力。它的作用点在受力物体与施力物体的接触点或接触面上。
但在很多实际问题的分析中,为了简化问题,我们往往可以把弹力的作用点移到物体的重心上。
●几种常见弹力的方向
下面我们就来一一认识这些常见弹力的方向吧。
如图1.3.5甲所示,书放在桌子上。由于书的挤压,桌子向下发生微小形变,要恢复原状,桌子对书产生向上的弹力F1,这个弹力又被叫做支持力。同时,书也会向上发生微小形变,并对桌子产生向下的弹力F2,又叫做压力。若将桌子倾斜,如图1.3.5乙所示,由于形变,桌子对书的支持力F3垂直于桌面向上,指向书;书对桌子的压力F4垂直于桌面向下,指向桌面。

图1.3.5 压力与支持力
3.你能总结出弹力产生的条件吗?
4.你知道弹力(压力、支持力、绳上的拉力等)的物理量符号吗?
5.在图1.3.6中,球会给绳子施加一个弹力吗?
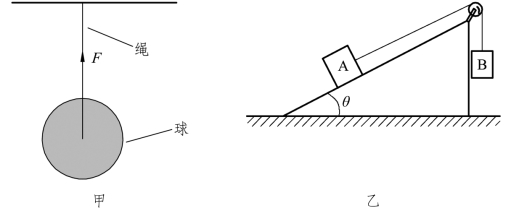
图1.3.6 绳上拉力
可见,支持力和压力的方向总是垂直于接触面,指向被支持或被压物体。
如图1.3.6甲所示,绳子悬挂小球时,绳子被拉长,绳子要收缩,恢复原状,会对小球产生向上的弹力,又叫拉力(绳中的弹力也常常被叫做张力)。因此,绳子上拉力的方向总是沿着绳子且指向绳子收缩的方向。你能在图1.3.10乙中分别画出A、B受到的绳子的拉力吗?
如图1.3.7甲所示,手压弹簧,弹簧被压缩,弹簧要恢复原长,对手施加一个向上的弹力。如图1.3.7乙所示,在一端固定的弹簧下挂一重物,弹簧被拉伸,弹簧要恢复原长,对重物施加一个向上的拉力。因此,弹簧弹力总是沿着弹簧轴线且指向弹簧恢复原长的方向。

图1.3.7 弹簧弹力计
6.你可以在图1.3.7乙中画出弹簧弹力的示意图吗?
7.你能根据这几种常见弹力的方向,总结出判断弹力方向的方法嘛?
综上所述,弹力的方向总是与物体恢复形变的方向相同。
●弹力的大小
由于产生弹力的物体材质、形状等是多种多样的,所以弹力的表现形式也是多种多样的。在以后学习中,我们将会探究多种求弹力大小的方法。
我们先来认识弹簧弹力的大小。从图1.3.8中可以看出,弹簧下悬挂的重物越多,拉力越大(弹簧弹力也越大),弹簧伸长越长。
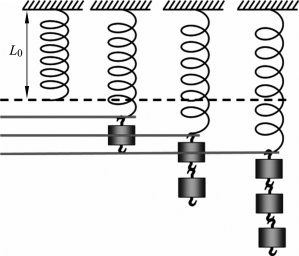
图1.3.8 弹簧伸长量与拉力
8.为什么拉力越大,弹簧弹力也越大?
那么弹簧弹力与伸长量满足什么定量关系呢?下面我们就来一起探究吧。
*实验探究
*弹簧弹力与伸长量的关系(胡克定律)
1.如图1.3.9所示,将铁架台放在桌面上(固定好),将弹簧的一端固定于铁架台的横梁上,在靠近弹簧处将刻度尺(最小分度为1 mm)竖直固定于铁架台上。

图1.3.9 实验装置
2.将弹簧挂在支架上,测量弹簧的原长L0。
3.在弹簧下端挂上钩码,待钩码静止后测出弹簧的长度L,求出弹簧的伸长量x和弹簧弹力F(等于所挂钩码的重力)。
4.改变所挂钩码的数量(每个钩码完全相同)和弹簧,重复上述实验,要尽量多测几组数据,将所测数据填写在表1.3.2和表1.3.3中。
9.弹簧伸长量和弹簧长度有什么区别?
表1.3.2 记录数据1(https://www.xing528.com)

表1.3.3 记录数据2

以弹簧伸长量为横坐标,弹力为横坐标,将表中的数据用描点法在图1.3.10中作出弹簧弹力随弹簧伸长量的变化图。
10.用图像法分析数据有什么好处?

图1.3.10 描点作图:F随x的变化关系
11.为什么发生弹性形变,才满足正比关系?
观察图像,可以得出结论:当弹簧发生弹性形变时,弹簧弹力与弹簧的伸长量成_____________。
英国科学家胡克在大量实验的基础上,找到了弹性体形变与力的关系,即著名的胡克定律:
弹簧发生弹性形变时,弹力的大小与弹簧的形变量(伸长量或压缩量)成正比,即
F=kx
其中,F表示弹力,单位N,x表示弹簧形变量,单位m,k表示弹簧的劲度系数,单位N/m。常说的弹簧“硬”或“软”,指的就是弹簧的劲度系数不同。
12.你会读劲度系数的单位吗?
想一想
如果把两根劲度系数分别为k1、k2的弹簧串联起来,如图1.3.11甲所示。那么串联后的弹簧劲度系数是多少呢?

图1.3.11 弹簧的串并联
如果把上面两根弹簧并联起来呢?如图1.3.11乙所示。并联后的弹簧劲度系数又是多少呢?
弹簧测力计
根据胡克定律,人们制成了弹簧测力计用来测量力的大小,如图1.3.12所示。

图1.3.12 弹簧测力计
●原理
在一定范围(弹性限度)内,弹簧受到的拉力越大,弹簧的伸长就越长。
●结构
如图1.3.13所示。

图1.3.13 弹簧测力计的结构
●使用
使用前:
1.看清量程、分度值。根据测量的力的大小和所需精度选择合适分度值和量程的测力计。一旦超量程,弹簧测力计可能损坏。
2.检查指针是否指在零刻度线处。若不在,应在待测力的方向上调零。
3.应适当用力来回拉动弹簧,防止其卡住或与外壳摩擦过大,影响测量。
使用时:
1.拉动弹簧时,避免弹簧与外壳接触。
2.应使弹簧测力计受力方向沿弹簧的轴线方向,即使测力计弹簧伸长方向与受力方向一致,如图1.3.14所示。

图1.3.14 沿力的方向拉动弹簧
3.待弹簧测力计示数稳定后再读数。读数时,视线要与刻度板表面垂直。
●其他测力计
除了弹簧测力计,人们根据不同的需要,还制造了各种各样的测力计来测量力的大小(见图1.3.15)。

图1.3.15 多种多样的测力计
13.什么是测力计?
14.你还见过哪些测力计?
自我评价(第2题选自人教版物理教材八年级下册,第4题选自人教版物理教材八年级下册)
1.关于弹力,下列说法中的正确是( )。
A.桌面受到水杯的弹力,方向垂直于桌面向上
B.放在桌面上的水杯受到的支持力是由于水杯发生弹性形变产生的
C.两个物体接触,不一定有弹力
D.物体发生的形变量越大,产生的弹力就一定越大
2.小强用弹簧测力器锻炼身体,刚拉开时没感到太费力,可是两手拉开的距离越大,越觉得费力。这是什么原因?
3.如图1.3.16所示的弹簧测力计,量程是___________,它的分度值是___________。若作用在挂钩上的拉力如图1.3.16所示,力的大小为___________。

图1.3.16
4.如图1.3.17所示,取A、B两个弹簧测力计,平放在水平桌面上,让它们互相钩挂在一起。然后用两只手分别向左、右拉。两个弹簧测力计的示数大小关系是什么?为什么?若把B固定在墙上,拉动A,两个弹簧测力计的示数大小关系又是什么?为什么?

图1.3.17
5.若将两根相同的弹簧并排使用,更_____(选填“难”或“易”)拉伸,则两根同样的弹簧并排使用做成的弹簧测力计比一根同样的弹簧做成的弹簧测力计量程_______(选填“大”或“小”)。
发条玩具中的弹力
你玩过图1.3.18中的这些玩具吗?

图1.3.18 发条玩具
图1.3.18 甲最早是在20世纪20年代,由上海康元制罐厂生产出的一款发条玩具“小鸡吃米”,又称“跳鸡”。它的内部没有电池,上足发条后,小鸡就会跳跃,做出啄米的动作。图1.3.18乙则是“跳蛙”,同样没有电池,上好发条,青蛙就可以跳起来了。风靡一时的发条玩具还有20世纪60年代的“小熊拍照”(见图1.3.19)。无需电池,靠发条驱动,小熊就能向左或向右旋转,并举起带闪光灯的照相机拍照。类似的还有机械手表(见图1.3.20),靠发条驱动,不用电池。

图1.3.19 小熊拍照玩具

图1.3.20 机械手表
其实,这些玩具和手表的工作原理都离不开他们内部一个神奇的构件——发条(见图1.3.21)。

图1.3.21 手表与发条
发条一般是用高弹性系数、高强度的合金材料制成的,在自由状态要下是一个螺旋形或S形的弹簧。上发条后,发条被条轴旋转卷紧。利用发条的弹性,可以让条盒转动,驱动装置。即发条利用弹力推动物体运动,将弹性势能转化为机械能。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




