科技文献老化的数学模型

1.负指数模型

英国著名情报学家布鲁克斯（B.C.Brookes）曾对科技期刊文献的老化问题进行过深入的研究。1970年，他提出科技期刊文献的被引用数量随时间推移的衰减过程近似服从简单的负指数模型，并利用微分方程推导出负指数模型的数学表达式。以后，许多科学家通过大量的统计数据证实这一规律确实存在。

为了推导该模型的数学表达式，布鲁克斯提出一条基本假设。

科技文献的使用价值在某一时间范围内均匀地减少。表现为相应文献被引用次数的均匀减少。在此假设之下，利用算术中求相对增长率或下降率的概念，可以建立文献老化过程的微分方程式。

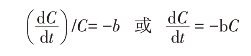
式中，C为引文的逐年分布量；b为老化衰减常数（0＜b＜1）；t为被引文献的出版年限。/C类似于算术中相对速率表达式，一般称为相对衰减率，在不太长的时期内可视为一个常数，求解以上微分方程式，可以得到：

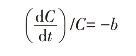
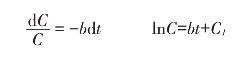
于是：

C（t）=e-bt+c1=ec1e-bt=C0e-bt

式中，常数C0为t=0时，文献的初始被引用量，随学科不同而异；-b为文献老化率。上面公式称为文献老化的负指数模型。通常，当文献达到被引峰值以后，便开始经历文献老化的衰减过程。

若以文献发表年龄为横轴，以现时正在利用的文献相对量为纵轴，可描绘出如图8.3所示的负指数曲线，称为“科技文献老化曲线”。

文献的年龄（足年为单位）T0.5为文献的半衰期(www.xing528.com)

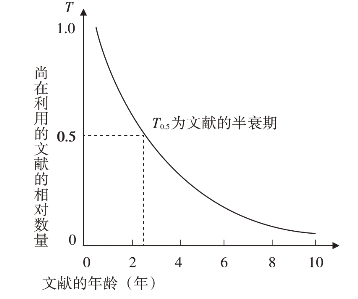
图8.3　科技文献老化曲线

统计数据分析表明，文献老化的负指数模型对于处理峰值以后的引文数据比较准确。这是因为当文献出版后较短时间内，e-b可视为一个常数，而随着时间的推移，e-b值将逐渐变大，即老化变慢，模型模拟的准确性也开始下降。设a=e-b，K=C0；Brooks文献老化的负指数模型可以写成以下形式：

C（T）=KaT

2.伯顿—凯普勒公式

1960年，美国某图书馆馆员伯顿（R.E.Burton）和物理学家凯普勒（R.W.Kebler）合作，对科技文献的老化问题进行了一系列研究。为了计算科技文献的半衰期，他们选择了物理、化学、机械工程等9个学科领域的期刊文献进行引文数据的统计分析和计算。结果发现9种不同学科的引文数据曲线形状上非常相似，同放射性物质的衰变曲线一样都是负指数曲线。于是他们导出这类曲线的一个标准公式，称为伯顿—凯普勒老化公式。

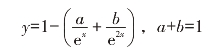
式中，y为被引文献累积百分数；x为被引文献出版年限（以10年为单位）；a、b为因学科、专业等而异的常数。因为伯顿—凯普勒老化公式包括了被引文文献峰值以前的引文文献数据，所以与负指数模型相比，该公式描述文献使用过程更加全面。

3.莫德列夫修正式

尽管伯顿—凯普勒公式描述文献使用过程比较全面，但该公式的模拟效果并不理想，与实际统计数据的误差较大。苏联文献计量学家莫德列夫在仔细研究了伯顿—凯普勒老化议程以后，于1982年提出了莫德列夫修正式：

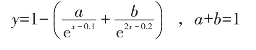
式中，变量与参数的意义与伯顿—凯普勒公式相同。

利用莫德列夫修正式，取得了比伯顿—凯普勒更好的模拟结果，但由于受原公式的限制，对某些科技文献的老化过程的处理也不够准确。同时，由于修正式形式比较复杂，也使计算比较繁复。