隔爆型旋转电机最小和最大径向间隙的计算

大家已经知道，隔爆型旋转电机轴与轴孔配合的最小径向间隙k至少应该大于0.05mm，最大径向间隙m不得大于标准规定的最大间隙值的三分之二（在滚动轴承的情况下）。这样的规定主要是防止在最不利的情况下轴与轴孔发生摩擦或者间隙过大，从而造成点燃危险。

因此，在结构设计时，设计人员应该计算这个k、m值，并向防爆电气产品检验机构提供计算结果；在防爆检验时，检验人员应该复核这个k、m值，确认制造商提供的数值符合要求。

隔爆型旋转电机轴与轴孔配合的最小径向间隙k、最大径向间隙m的计算，实际上就是一种尺寸链的计算。

1.尺寸链的一般概念

最小径向间隙k、最大径向间隙m的计算属于尺寸链计算，这里简单地讨论一下与此有关的尺寸链的基本概念。

（1）有关的术语

这里介绍几个与计算最小径向间隙k、最大径向间隙m有关的尺寸链术语：

●尺寸链——在机器装配或零件加工过程中由相互连接的一系列尺寸形成的封闭尺寸组。

●环——组成尺寸链的每一个尺寸。

●封闭环——在机器装配或零件加工过程中最后形成的尺寸链中的一环。

●组成环——尺寸链中对封闭环有影响的所有环，即这些环中任一环的变动必然会影响封闭环的变动。在其他条件一定的情况下，若某一环的增加会引起封闭环的增加，减小会引起封闭环的减小，则这一环被定义为“增环”；若某一环的增加会引起封闭环的减小，减小会引起封闭环的增加，则这一环被定义为“减环”。

●派生尺寸链——一个尺寸链的封闭环是另一个尺寸链的组成环的尺寸链。

●传递系数——各个组成环分别对封闭环产生影响程度大小的系数，用符号ζ_i表示。对于增环，ζ_i为正值；对于减环，ζ_i为负值。

●平均偏差——实际偏差的平均值，用符号X_i表示（图3.29）。

●中间偏差——上极限偏差与下极限偏差的平均值，用符号Δ_i表示（图3.29）。

●相对分布系数——表征尺寸分布曲线分散性的系数，用符号k_i表示（图3.29）。

●相对不对称系数——表征尺寸分布曲线不对称程度的系数，用符号e_i表示（图3.29）。

●统计公差——按照封闭环和组成环统计特性计算的封闭环和组成环的公差，这里简称为“公差”，用符号T_i表示（图3.29）。

这里应该指出的是，在上述各个表示符号中的下脚标i表示环的序号：封闭环用0表示，例如，封闭环的中间偏差表示为Δ₀；组成环用1，2，3…表示，例如，第1组成环的中间偏差表示为Δ₁，等等。

从图3.29可以看出，公称尺寸（L）、上、下极限尺寸（L_max、L_min）、中间偏差（Δ）、上极限偏差（ES）、下极限偏差（EI）和公差（T）等尺寸之间存在的相关关系。

（2）尺寸链的计算

尺寸链的计算，主要是计算封闭环与组成环的公称尺寸、公差及极限尺寸之间的关系。这样的计算分为正计算、反计算和中间计算。所谓正计算，就是已知各个组成环的相关参数来计算封闭环的相关参数，实际上，就是一种校核计算；反计算，就是已知封闭环的相关参数来计算（分配）各个组成环的相关参数，实际上，就是一种设计计算；中间计算，就是已知封闭环和部分组成环的相关参数来计算另一部分组成环的相关参数，具有正计算和反计算的一些特征。

图3.29 尺寸链中尺寸分布曲线

a）正态分布 b）瑞利分布

在讨论最小径向间隙k、最大径向间隙m的计算时，我们采用尺寸链的正计算，即校核计算。这里将使用以下公式。

●封闭环公称尺寸计算公式：

式中 ζ_i——某一组成环的传递系数，对于增环，ζ_i为正值，对于减环，ζ_i为负值；

L_i——某一组成环的公称尺寸。

●封闭环中间偏差计算公式：

式中 ζ_i——同式（3.20）；

Δ_i——某一组成环的中间偏差；

e_i——某一组成环的相对不对称系数，对于正态分布，e_i=0；

T_i——某一组成环的公差。

●封闭环公差计算公式：

式中 ζ_i，T_i——同式（3.20）、式（3.21）；

k_i——相对分布系数。

●封闭环极限偏差（上极限偏差记作ES₀，下极限偏差记作EI₀）计算公式：

式中 Δ₀，T₀——同式（3.21）、式（3.22）。

●封闭环极限尺寸（上极限尺寸记作L_max，下极限尺寸记作L_min）计算公式：

式中 L₀，ES₀，EI₀——同式（3.20）、式（3.23）。

2.最小径向间隙k和最大径向间隙m的计算

（1）计算公式

最小径向间隙k和最大径向间隙m的计算，就是采用尺寸链的正计算来计算封闭环的各个参数以校核设计尺寸的正确性。分析可知，封闭环的下极限尺寸L_min就是最小径向间隙k，上极限尺寸L_max就是最大径向间隙m。

因而，整理上述相关各式后，便得到

式中 L₀，Δ₀，T₀——同前述各式。

当按照式（3.20）、式（3.21）、式（3.22）分别计算出封闭环的公称尺寸、中间偏差和公差后便可以按照式（3.25）和式（3.26）计算得到最小径向间隙k和最大径向间隙m。

（2）计算示例

【例3.9】 这里以YB系列中心高为H250的隔爆型三相异步电动机为例，通过分析它的轴贯通部分尺寸链的组成，来求解隔爆型旋转电机的最小径向间隙k和最大径向间隙m。

1）建立尺寸链

在隔爆型旋转电机中，影响最小径向间隙k和最大径向间隙m的因素很多，轴贯通部分（图3.30）就有以下主要因素：

●轴承内盖上轴孔内径（半径）的偏心，记作A₁。

●轴上轴承内盖凸台外径（半径）的偏心，记作A₂。

●轴承室内径与轴承内盖上止口外径的装配间隙引起的偏心，记作B₁。

●轴承室内径与轴承外径的装配间隙引起的偏心，记作B₂。

●轴承径向游隙引起的偏心，记作B₃。

●轴承内盖上轴孔对止口的径向全跳动引起的偏心，记作B₄。

●轴上轴承内盖凸台外径对两端轴承内盖凸台中心连线的径向全跳动引起的偏心，记作B₅。

从尺寸链分析的角度看，这些因素就是尺寸链的环，构成了尺寸链。根据上述这些主要因素，可以画出尺寸链图，如图3.31所示。(www.xing528.com)

图3.30 H250YB系列隔爆型三相异步 电动机轴贯通部分示意图

图3.31 轴贯通部分的尺寸链图

在图3.31中，A₀为封闭环；A₁、A₂、A₃（B₀）为组成环，其中，A₃即派生尺寸链B的封闭环B₀。

分析可知，在组成环中，A₁为增环，即，在其他条件不变的情况下，随着A₁的增加，封闭环A₀也增加，随着A₁的减小，封闭环A₀也减小；其他各环均为减环，即，在其他条件不变的情况下，随着某一环的增加，封闭环A₀则减小，随着某一环的减小，封闭环A₀则增加。

2）各组成环参数数值的确定

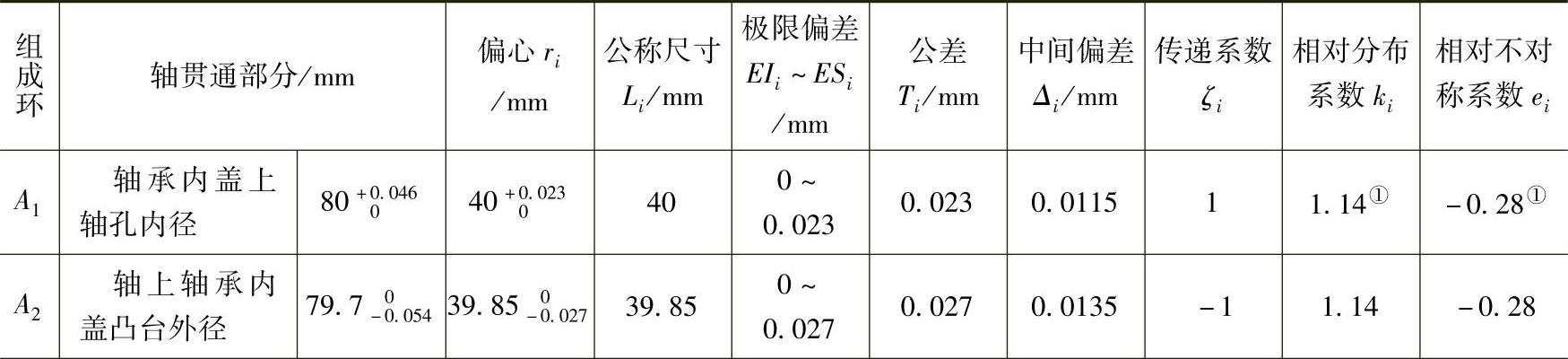
对于YB系列中心高为H250的隔爆型三相异步电动机，轴贯通部分的设计数据和组成环数据如表3.13所示。

表3.13 轴贯通部分设计数据和组成环数据

（续）

注：公称尺寸即标称尺寸，这里是指偏心后的标称尺寸。通常情况下，轴承室内径、轴承外径、轴承内盖上凸台外径（如果存在的话）的公称尺寸是相等的，所以偏心后的公称尺寸等于0。

①在大批量生产且加工工艺相对稳定的情况下，封闭环按正态分布，则k_i=1，e_i=0；组成环按瑞利分布，则k_i=1.14，e_i=-0.28。

②轴承径向游隙通常是指轴承处于自由状态时的数值。装配后由于过盈配合使得这个游隙值减小。由于过盈量大小不同，这个减小量也是不同的。装配后游隙的减小量一般按最小过盈量的70%计。例如，本例中最小过盈量为0.002，按70%计算，游隙减小为0.0286，故偏心为0.0143。

3）最小径向间隙k和最大径向间隙m计算

按照尺寸链的计算方法，首先，计算派生尺寸链（B）封闭环B₀（A₃）的公称尺寸、中间偏差和公差。将表3.13中相关数据代入式（3.20）、式（3.21）、式（3.22）中计算即可得到

●公称尺寸L_0.B=0mm。

●中间偏差Δ_0.B=-0.044mm。

●公差T_0.B=0.072mm。

接着，计算公称尺寸链（A）封闭环的公称尺寸、中间偏差和公差。将派生尺寸链（B）封闭环的上述计算结果和表3.13中相关数据代入式（3.20）、式（3.21）、式（3.22）中计算即可得到

●公称尺寸L₀=40mm-39.85mm=0.15mm。

●中间偏差Δ₀=0.053mm。

●公差T₀=0.091mm。

最后，按照式（3.25）和式（3.26）计算公称尺寸链（A）封闭环的下极限尺寸L_min和上极限尺寸L_max，即最小径向间隙k和最大径向间隙m：

k=0.15mm+0.053mm-1/2×0.091mm=0.1575mm≈0.16mm

m=0.15mm+0.053mm+1/2×0.091mm=0.2485mm≈0.25mm

（3）讨论

①在计算示例中提出的最小径向间隙k和最大径向间隙m的计算（校核）方法，是按照YB系列中心高为H160～H280的隔爆型三相异步电动机轴贯通部分的已有设计结构，通过尺寸链的计算方法提出来的，具有一定局限性和某些通用性。对于其他的隔爆型旋转电机，由于轴贯通部分的结构不同，计算所使用的参数可能有所不同，但是，分析和计算方法以及一些系数的选择（例如传递系数、相对分布系数和相对不对称系数），应该是通用的。人们可以参照这里的思考方法，运用尺寸链的计算原则提出适于相应结构的计算参数，完成这种计算。

②在计算示例中提出的最小径向间隙k和最大径向间隙m的计算（校核）方法，是将设计数据转化为尺寸链计算时所需的参数进行的（称为“转换法”）。下面提出直接采用设计数据进行这种计算的计算方法（称为“直接法”）。

现将表3.13转化为表3.14，就可以直接采用设计数据进行这种计算。

表3.14 轴贯通部分设计参数和组成环参数

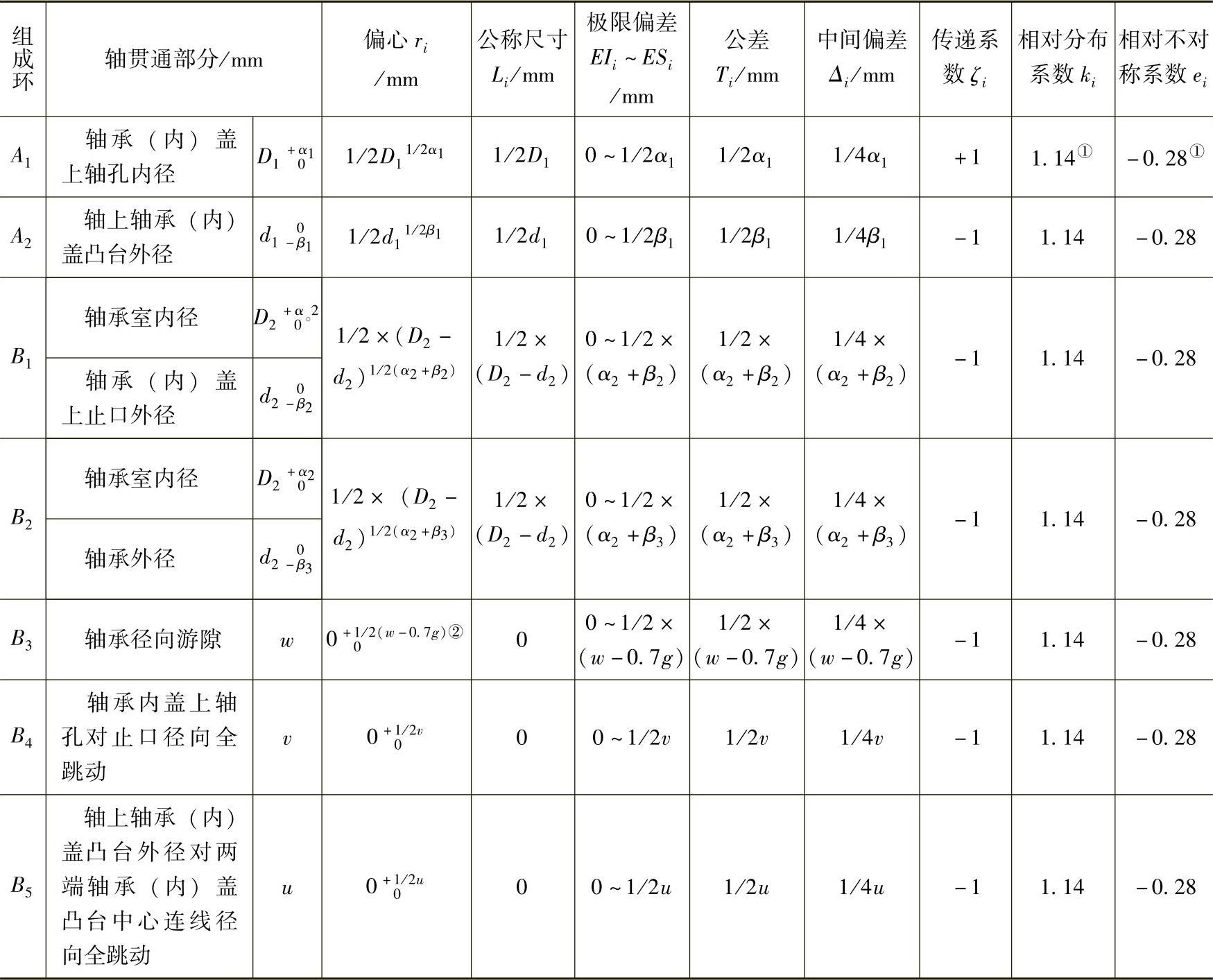
注：国家标准GB/T 5847—2004《尺寸链 计算方法》指出，偏心或径向跳动趋于瑞利分布，因而，k=1.14，e=-0.28。

①，②同表3.13。

按照表3.14将式（3.20）、式（3.21）和式（3.22）转化为直接使用设计数据进行公称尺寸、中间偏差和公差计算的计算式。

首先，计算派生尺寸链（B）封闭环（B₀）的公称尺寸、中间偏差和公差。

●公称尺寸为

L_0.B=0 （3.27）

●中间偏差为

Δ_0.B=-0.18（2α₂+β₂+β₃+w+v+u-0.7g） （3.28）

●公差为

然后，将式（3.27）、式（3.28）、式（3.29）作为公称尺寸链（A）的组成环的数据，计算公称尺寸链（A）封闭环（A₀）的公称尺寸、中间偏差和公差。

●公称尺寸为

L₀=1/2（D₁-d₁） （3.30）

●中间偏差为

其中，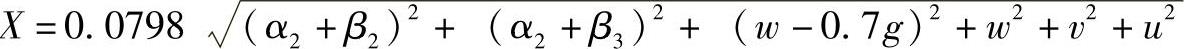

●公差为

这里需要指出的是，上述各式中符号的含义参见表3.14。式中的α₁，α₂，β₁，β₂，β₃均为绝对值（mm）；g为轴与轴承装配的最小过盈量（mm）。

这样，人们就可以将式（3.30）、式（3.31）和式（3.32）的计算结果代入式（3.25）和式（3.26）中直接求得最小径向间隙k和最大径向间隙m。

事实上，使用上述讨论的两种计算方法（转换法和直接法）计算得到的结果是完全一致的，因为计算方法的实质是一样的，只是表现的形式不同而已。

③在使用直接法进行计算时，由于各种电机轴贯通部分的结构不同，人们可以将式（3.31）和式（3.32）中的参数去掉（或增添）几个，然后，再按照式（3.30）和这些式子进行这种“直接”计算。

例如，中心高为H80的YB系列隔爆型三相异步电动机（图3.32）。轴贯通部分的已有设计尺寸为：轴承盖上轴孔内径D₁=ϕ20^+0.035₀，轴上轴承盖凸台外径d₁=ϕ19.75_-0.015⁰，轴承室内径D₂=ϕ47^+0.025₀，轴承外径d₂=ϕ47_-0.011⁰，轴承径向游隙w=0.020，轴上轴承盖凸台外径对两端轴承盖凸台中心连线径向全跳动u=0.010。

由于这种电动机没有轴承内盖，所以就没有轴承室内径与轴承内盖上止口外径的配合、轴承内盖上轴孔对止口径向全跳动。于是，可以在式（3.31）和式（3.32）中除去相关参数后计算中间偏差和公差。

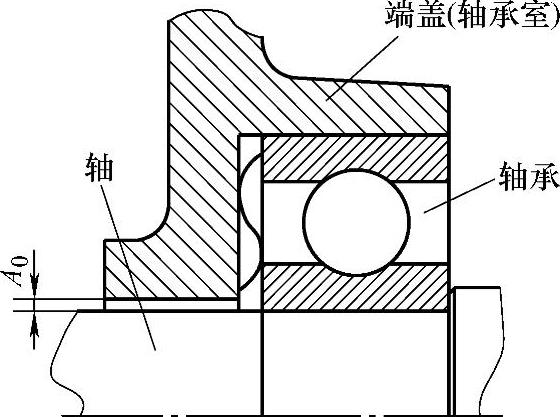
图3.32 H80YB系列隔爆型三相异步电动机轴贯通部分结构示意图

将有关尺寸参数代入这些式子后计算得到它的公称尺寸L₀=0.125mm，中间偏差Δ₀=0.0186mm，公差T₀=0.035mm。

最后，将所得到的L₀、Δ₀、T₀代入式（3.25）、式（3.26）中计算即可得到H80YB系列隔爆型三相异步电动机的最小径向间隙k和最大径向间隙m。即

k=0.126mm，m=0.161mm。

总之，从上述计算可以看出，最小径向间隙k和最大径向间隙m的计算是较为复杂的，但是，从防爆安全性能上看，却是十分必要的，应该引起人们的注意。