如何计算氢气爆炸压力？-从混合物的初始压力和温度出发

隔爆外壳应该具有耐爆性能，是指隔爆外壳应该能够承受内部爆炸性气体-空气混合物发生爆炸时产生的爆炸压力作用而不损坏，也就是说，应该具有足够的机械强度。

根据燃烧与爆炸的热理论可知，爆炸性气体-空气混合物在密闭容器内点燃爆炸时要产生高温和高压。绝热压缩定律指出，爆炸性气体-空气混合物发生爆炸时产生的温度和压力随着火焰从点燃源向器壁的传播而减小。在爆炸过程中，点燃源处的温度最高，火焰面（即火焰表面）的温度最低。

1.可燃性气体的爆炸压力

爆炸性气体-空气混合物在发生爆炸时产生高压是可燃性气体的一个极其重要的特性。在密闭容器中发生爆炸时，在绝热情况下，爆炸压力可以用下式表示：

式中 P——爆炸压力（MPa）；

P₀——初始压力（MPa）；

T——可燃性气体的燃烧温度（K）；

T₀——爆炸性气体-空气混合物的初始温度，即273+t₀（K）；

t₀——初始温度（℃）；

m——爆炸后爆炸生成物的分子总数；

n——爆炸前爆炸性气体-空气混合物的分子总数。

在化学计算浓度条件下，燃烧（爆炸）反应进行得很充分，产生的热量最大，爆炸生成物实质上主要是不参与反应的氮（N₂），以及水（H₂O）、二氧化碳（CO₂）、有关元素的氧化物等。此时，爆炸产生的压力最大。混合物中可燃性气体的浓度低于或高于化学计算浓度，爆炸压力都会减小。由于各种可燃性气体-空气混合物的化学计算浓度不同，燃烧温度不同，所以，在一定条件下爆炸压力也是不同的。

通常，式（3.1）被称为爆炸压力计算公式。

这里以乙炔为例，使用式（3.1）来计算它的爆炸压力。

【例3.1】 计算以常温常压（即20℃、101.325kPa）为标准环境条件。通常情况下，空气中氧气与氮气的比例约为1∶3.7，也就是说，在空气中只要有一个氧气分子就会同时有3.7个氮气分子。大家知道，乙炔在空气中发生爆炸时的化学反应式为

2C₂H₂+5O₂=4CO₂+2H₂O

由此可知，在这个反应中有5个氧气分子参与了反应。因而，在其中同时有18.5个氮气分子也参与了“反应”的全过程。于是，爆炸发生前参与反应的分子总数n=25.5，爆炸发生后爆炸生成物的分子总数m=24.5。乙炔的燃烧温度T=2893K。将这些相关数据代入式（3.1）计算得到乙炔的爆炸压力为

P=0.101325×[2893/（273+20）]×（24.5/25.5）MPa≈0.96MPa

依照同样的方法，通过理论计算可以获得在标准环境条件下发生爆炸时甲烷的爆炸压力为P≈0.80MPa，丙烷的P≈0.85MPa，乙烯的P≈0.88MPa，氢气的P≈0.73MPa。

这里需要指出的是，在这种计算中，我们忽略了空气中其他惰性气体的作用。计算可知，这种忽略在误差容许的范围内。

实际上，计算和试验表明，对于大多数可燃性气体-空气混合物来说，如果混合物的初始压力、初始温度为正常的大气环境条件的话，那么，爆炸压力通常不超过1.0MPa。例如，大量的试验测试表明，氢气（H₂）在试验室环境、浓度为32%的条件下发生爆炸时测得的爆炸压力约为0.73MPa。

从式（3.1）中可以看出，爆炸性气体-空气混合物在一定形状的外壳内发生点燃爆炸时产生的爆炸压力，不仅与参与反应的可燃性气体的燃烧温度、爆炸前后的分子总数有关，而且还与混合物的初始压力、初始温度有关。燃烧温度和分子总数是由可燃性气体的固有特性决定的，而初始压力和初始温度是随环境条件变化的。

下面讨论一下混合物的初始压力和初始温度对爆炸压力的影响。

（1）初始压力对爆炸压力的影响

混合物的初始压力对爆炸压力的影响是很大的。由式（3.1）可知，随着初始压力的增加，爆炸压力呈线性地增加。

这里以氢气为例（对于其他可燃性气体，请读者自行计算），按照式（3.1）进行理论计算，得到表3.1所示数据（初始温度按环境温度20℃计，即293K）。

表3.1 氢气-空气混合物的初始压力与爆炸压力的关系

注：表中的初始压力为绝对压力。

实际试验证实了这一点。人们在4L的标准球形外壳内充满浓度为32%的氢气-空气混合物，以不同的压力值（相对压力，即压力表表压）对混合物进行预压，然后点燃爆炸。试验结果如图3.1所示。

从图3.1中可以看出，当没有对试验气体混合物进行预压（p₁=0），即混合物处于大气压力条件下时，试验测得的爆炸压力约为p₀=0.73MPa。

这里需要指出的是，对于氢气，上述的爆炸压力的理论计算值和试验测试值均为0.73MPa，这是一种巧合。理论计算值和试验测试值有着不一样的概念。

从图3.1中可以得到解析方程

P=p₀+Kp₁ （3.2）

式中 P——在不同的预压压力条件下实际测得的爆炸压力（MPa）；

p₀——当混合物处于试验室大气条件下测得的爆炸压力（MPa）；

K——系数；

p₁——预压压力（MPa）。

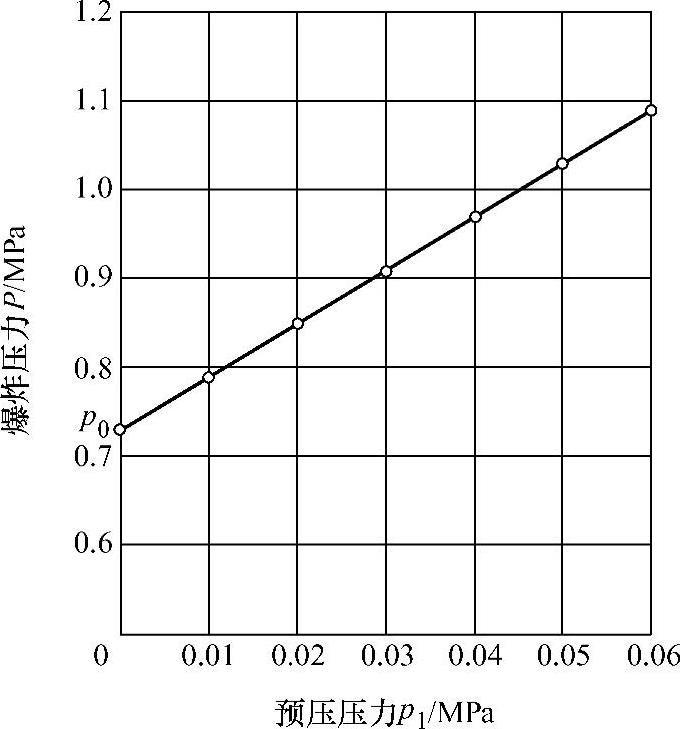
图3.1 预压压力与爆炸压力的关系

对于氢气-空气混合物来说，按照图3.1所示的试验曲线计算可知，式（3.2）中的系数K≈6。对于每一种可燃性气体-空气混合物，系数K都有一个对应值。

通常，式（3.2）被称为预压压力计算公式。(www.xing528.com)

理论分析与计算指出，对于各种可燃性气体-空气混合物来说，它们在大气环境条件下发生爆炸时所产生的爆炸压力，既符合式（3.1），也满足式（3.2）；只是在式（3.2）中K值是不同的。例如，在采用其他参数为常温常压下的计算值时，计算可知，K的理论值为：对于甲烷-空气混合物，K≈7.8；丙烷-空气混合物，K≈8.5；乙烯-空气混合物，K≈8.7；乙炔-空气混合物，K≈9.5；氢气-空气混合物，K≈7.2。

在实际应用中，可以按照式（3.2）获得任意预压压力下的任何碳氢化合物的爆炸性气体-空气混合物的爆炸压力。

【例3.2】 这里仍然以氢气为例来计算混合物在环境温度（20℃）条件下预压压力为p₁=0.05MPa时的爆炸压力。p₀、K取试验数据，即p₀=0.73MPa，K=6。将这些数据代入式（3.2）计算即可得出此时氢气的爆炸压力为

P=0.73MPa+6×0.05MPa=1.03MPa

从图3.1可以看出，计算数据与试验数据具有令人满意的拟合性。

这里的计算结果也可以通过式（3.1）和式（3.2）用纯理论计算的方法予以验证。所谓纯理论计算是指计算采用的数据都是理论值，不考虑实际试验时得到的试验数据。

当使用式（3.1）计算时，令P₀=（0.101+p₁）=（0.101+0.05）MPa。将它代入式（3.1）计算便得到此时的爆炸压力P≈1.09MPa。

当使用式（3.2）计算时，令p₀=0.73MPa，K=7.2，p₁=0.05MPa。将这些数据代入式（3.2）计算便得到此时的爆炸压力P=1.09MPa。

从这些计算结果可以看出，式（3.1）和式（3.2）在理论上是一致的，而且理论计算值（1.09MPa）和试验计算值（1.03MPa）基本上也是一致的。二者之差是由系数K引起的，与试验条件有关。大量的理论计算表明，这里的结论是正确的。

在隔爆外壳的耐爆性能试验时，为了得到预期的试验爆炸压力，人们可以使用式（3.2）来计算所需的预压压力值。只是在这种计算中人们必须找出相应的p₀和K值。

这里需要指出的是，对于氢气-空气混合物来说，在式（3.2）中，K≈6是从图3.1中的试验曲线计算求得的，它与理论计算值有一个差。这一点是很容易理解的。在实际的实验室试验中，很多因素在影响着测量的准确度，例如，试验气体的纯度和浓度，试验外壳的形状和净容积，测量仪器的精度，以及试验室的海拔和环境温度，等等。这就是试验值不同于理论值的原因所在。正因为如此，在实际应用中，建议采用试验曲线给出的相应值。

（2）初始温度对爆炸压力的影响

混合物的初始温度对爆炸压力同样具有明显的影响作用。由式（3.1）可知，当混合物的初始温度增加时，则爆炸压力减小；随着初始温度的减小，爆炸压力随之增加。这是一种反比例关系。

这里以初始压力为1个大气压力为计算条件，同样以氢气-空气混合物为例来计算不同初始温度时的爆炸压力。理论计算值如表3.2所示。

表3.2 氢气-空气混合物的初始温度与爆炸压力的关系

各种可燃性气体-空气混合物在发生爆炸时都具有这种性质，只是数值不同而已。这就告诉人们，假若所设计、制造的隔爆型电气设备预期使用在寒冷的低温环境中，那么，它的隔爆外壳就必须具有更高的机械强度（和较小的结构间隙）。

上述的这些理论计算数据和实际试验数据是十分有用的，是进行隔爆型电气设备隔爆结构设计和型式试验的基本理论依据。

（3）影响爆炸压力的其他因素

在实际应用中，除了上述可燃性气体的物理-化学性质和混合物的初始压力、初始温度对爆炸压力产生的影响外，外壳的大小、形状和点燃源的位置、强度对爆炸压力也具有很大的影响。

1）外壳大小、形状的影响

试验研究指出，爆炸性气体-空气混合物在密闭外壳中发生爆炸时，在其他试验条件相同的情况下，爆炸压力随外壳净容积的增加而略有增加，而且这种关系是非线性的。试验指出，在净容积为0.5L的球形外壳内发生爆炸时产生的爆炸压力，仅比在净容积为116L的球形外壳内发生爆炸时产生的爆炸压力小十分之一个大气压力。

此外，试验发现，外壳的形状对爆炸压力有一定的影响。当同一种混合物在同样大小容积、不同形状的外壳内发生爆炸时，测得的爆炸压力是不同的。

外壳形状对爆炸压力的影响是这样的，球形外壳中产生的爆炸压力大于正方体外壳的，正方体外壳中产生的爆炸压力大于圆筒体外壳的，圆筒体外壳中产生的爆炸压力大于长方体外壳的。这种现象可以用燃烧爆炸的热理论做出解释。这是因为，在同样大小容积的情况下，球形外壳的内表面积小于正方体外壳的，正方体外壳的内表面积小于圆筒体外壳的，圆筒体外壳的内表面积小于长方体外壳的，所以，当发生爆炸时爆炸产生的热量在球形外壳内壁上损耗的最少，而在长方体外壳内壁上损耗的最多。因而，爆炸压力就不同。

2）点燃源位置、功率大小的影响

试验研究指出，点燃源的位置和功率大小对爆炸压力有一定的影响。

试验指出，在球形外壳的情况下，点燃源位于球形中心时产生的爆炸压力最大，点燃源离开中心越远，爆炸压力越小。

试验还指出，点燃源的功率对爆炸压力的影响很大。例如，在发生弧光短路（这时点燃源发出的能量相当大）的情况下，在容积为0.4L的球形外壳（间隙0.1mm）中，点燃甲烷-空气混合物时得到了1.3MPa的爆炸压力；在其他试验条件相同的情况下，用放电火花点燃时爆炸压力则小得多。

从上述可知，隔爆外壳必须具备足够的机械强度，才能承受内部发生爆炸时产生的爆炸压力的冲击作用。否则，隔爆外壳的破损将导致外壳周围爆炸性气体-空气混合物的点燃爆炸。由于隔爆外壳的结构和强度设计不合理，在正常的耐爆性能试验中，外壳被破坏的例子比比皆是。

2.绝缘材料热分解可能造成的危险

除了上述情况之外，还有一点也必须引起人们的注意，那就是，在隔爆外壳中，由于电弧的作用，使电气设备内的电气绝缘部件发生热分解，产生大量的气体（例如，氢气、甲烷、一氧化碳等）；它们积聚在设备的外壳内，形成一种积聚压力。试验指出，在某种条件下，这个压力竟达2MPa。

绝缘部件热分解时产生的气体的积聚压力可以用下式计算求得

P=P₀+CAt₀/V （3.3）

式中 P——积聚压力（MPa）；

P₀——外壳内气体被加热时产生的压力（MPa）；

C——1kW·s电弧能量分解出来的气体体积，通常为4～6cm³；

A——电弧功率（kW）；

t₀——电弧的持续时间（s）；

V——外壳的净容积（cm³）。

在这种情况下，除积聚压力对外壳的作用外，如果在电气设备的隔爆外壳内可燃性气体混合物达到爆炸极限时发生点燃爆炸的话，那么，在积聚压力[即式（3.2）中的预压压力p₁]的作用下这个爆炸压力将是十分大的，对外壳极具破坏作用。

除此之外，电气绝缘材料的热分解所产生的各种可燃性气体，还会改变隔爆外壳内爆炸性气体-空气混合物的成分，从而也改变着这种混合型可燃性气体的爆炸性质，当然也影响着隔爆外壳的隔爆性能。

由此可见，由电弧作用而使绝缘材料发生热分解产生的气体在隔爆外壳内的积聚，有时候是十分危险的。在隔爆外壳设计时，人们必须给以应有的注意。