当自由度发生改变时,双层结构预测控制的算法原理并不改变。以下给出一些常见的变自由度及处理措施:
(1)如果MV在硬约束界上“卡边”,包括当前值和稳态目标值都停留在约束界上,可将该MV变为DV,相应的MV约束不再考虑;
(2)如果MV的控制权被操作人员移除,则该MV变为DV,相应的MV约束不再考虑;
(3)如果CV的控制权被操作人员移除,则相应的CV约束不再考虑;
(4)如果SSTC在最高优先级无法通过放松的方法使可行域为非空,则找出引起不可行的CV,并移除之,相应的约束不再考虑。方法是:离线时将CV硬约束按照优先级排名(每个CV的幅值上、下限硬约束在同一个优先级),在线时,如果SSTC的最高优先级的优化问题不可行,则按照优先级次序(采用升序策略)判断可行性,则造成不可行的硬约束对应的CV即为需要移除的;如果造成不可行的是CV的稳态变化约束[见式(4-13)、式(5-21)、式(6-31)],则移除该约束而不移除对应的CV;
(5)发生了MV、CV的增减后,通过判断加权CV之间的共线性,来确定是否减少CV的数量和对应的约束。
通常某些大的干扰可以引起(4)。CV由于大的干扰无法控制,在SSTC和动态控制中都可检验,其中在SSTC中表现为可行域为空,而在动态控制中表现为未来的动态预测值超约束。如果长时间出现某些CV不能控制,应做异常处理,即停止运行MPC。实际上,如果SSTC对yss(k)的计算结果持续超过操作约束,参考文献[41]和参考文献[31]都建议作为一种异常处理,因为这种情况表示对大的干扰失去了抑制能力。
对(5),通过计算/改变无约束最小二乘问题的Hessian矩阵(见注解6.4)的条件数,使得动态控制模块的优化问题有合适的解。以第4章为例,这相当于考虑矩阵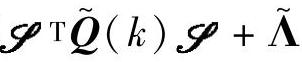 Λ~的条件数,如果无约束最小二乘问题的条件数过大,某些MV可能大幅度变化,对实际生产非常不利。假设条件数过大,有两种措施,其一是临时增大/改变
Λ~的条件数,如果无约束最小二乘问题的条件数过大,某些MV可能大幅度变化,对实际生产非常不利。假设条件数过大,有两种措施,其一是临时增大/改变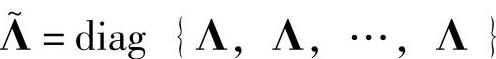 使条件数减小;其二是对被控变量进行重组。
使条件数减小;其二是对被控变量进行重组。
下面考虑第二种措施。在k时刻,(https://www.xing528.com)
yss(k)-Gff(k)=Guuss(k) (10-7)
其中, 。由于不同的CV有不同的加权,故处理如下方程:
。由于不同的CV有不同的加权,故处理如下方程:
Q(k)1/2yss(k)-Q(k)1/2Gff(k)=Q(k)1/2Guuss(k) (10-8)
对Q(k)1/2Gu进行SVD分解,得到
其中,diag{U1,U2}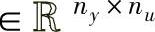 。如果ny≠nu,则选择U2为方阵。由式(10-9)进一步近似得到
。如果ny≠nu,则选择U2为方阵。由式(10-9)进一步近似得到
将式(10-10)等价地表示为
y′ss(k)-G′ff(k)=G′uuss(k) (10-11)
这时CV变成y′=ΣT1Q(k)1/2y,故所有对应于y的目标值、约束等分别转化为关于y′的目标值、约束;{Gu,Gf}替换为{G′u,G′f}(如果采用DMC,则所有的{Sui,Sfi}替换为{ΣT1Q(k)1/2Sui,ΣT1Q(k)1/2Sfi})。如果yss(k)的一部分有理想值,而剩下的部分没有理想值,则y′ss(k)=ΣT1Q(k)1/2yss(k)不再有理想值。另外,针对y′的动态控制加权临时取为单位阵。这一措施使得实时的加权稳态增益矩阵Q(k)1/2Gu的条件数在适当范围内,因为如果条件数过大,则某些CV之间设定值的微小差异可能造成部分MV大幅度变化,对实际生产非常不利。严格地讲,处理矩阵Q(k)1/2Gu的条件数并不等价于处理 的条件数。第二种措施在具体采用时,不用先观察
的条件数。第二种措施在具体采用时,不用先观察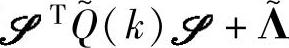 的条件数。
的条件数。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




