无静差控制动态稳定性研究现状

本书的定位是主要研究和介绍工业预测控制算法。通常，是需要区分“控制算法”和“控制科学中的数学问题”的。控制算法的好与坏应决定于其实用性，对“控制科学中的数学问题”，解决得好与差主要取决于其正确性和原创性。通常，控制算法的论述强调其能够实现的部分，但对精确的假设条件等可能不够重视。人们容易笼统地把“控制算法”和“控制科学中的数学问题”统称为控制理论，但是两者是有本质的区别的。类似稳定性、最优性等研究，是建立在严格的假设的基础上的（很多时候，这些假设没有被明确地说明，但应为研究者所熟知），属于控制科学中的数学问题。预测控制的研究，也应特别注意“控制算法”和“控制科学中的数学问题”之区别，达到一种默认或共识的程度。由宽到窄的词语分别为控制论、控制理论、预测控制、预测控制中的数学问题；或者：控制论、控制理论、预测控制、工业预测控制算法；或者：数学、应用数学、数学控制理论、预测控制中的数学问题。

在第1章，已经明确地指出：由“RTO+双层结构MPC+PID+被控对象”组成的系统，是一个多周期、多目标、含各层次模型、优化的复杂系统，其理论问题（如稳定性）远未解决，是个开放性的难题。这里，我们进一步分析其难度：

•多周期：RTO为小时级周期且不固定，双层结构MPC为分钟级周期且一般是固定的，PID为秒级周期。比较合理的做法是将PID作为被控系统的一部分，并针对被控系统离散时间模型（周期同双层结构MPC）进行研究；

•多目标：RTO、SSTC和动态控制各有自己的目标函数，且SSTC可能具有一系列的目标函数；

•含各层次模型：RTO采用稳态非线性模型，SSTC采用稳态线性模型，动态控制采用动态线性模型；

•含各层次优化：RTO采用非线性优化，SSTC采用线性和二次规划，动态控制采用二次规划。

首先，讨论工业预测控制算法实现中如何保证动态稳定性。简单地说，是通过试调控制器参数，用仿真的方法观察是否稳定的。这里给出简要的规则：

（1）最适宜调整的参数：预测时域（P，N）、控制时域（M，N_c）。增大预测时域和减小控制时域经常容易重获稳定性，但是增大预测时域会增加计算量，而减小控制时域会使得到的控制作用更保守；

（2）适宜调整的参数：输出跟踪误差加权矩阵Q（k）、输入增量加权矩阵Λ、动态控制模块中CV软约束松弛量加权中的调整系数ρ。对开环稳定和仅含积分型不稳定模态的模型，增大Λ容易重获稳定性，但会使得到的控制作用更保守。可有选择性的增大某个CV的Q（k）分量，使这个CV的波动减小。ρ根据Q（k）和Λ的幅值进行调整，体现对松弛量的适度惩罚；

（3）可调整的参数：MV的稳态速率约束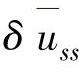、MV的变化速率约束Δu、CV的稳态速率约束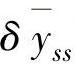或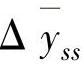。对开环稳定模型，减小这些数值都使得系统更容易稳定，但控制更倾向于保守；

（4）谨慎调整的参数：开环预测模块中的平滑系数α、旋转因子σ、第一类积分CV的折算系数ξ、动态控制模块中加权的转换区域边界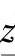和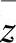、积分型CV设定值速率κ和安全时域L；

（5）特别谨慎调整的参数：模型时域N、控制周期或采样周期、Kalman滤波的可调参数、人工干扰模型参数G_p和G_d、积分标识（某个CV选择为稳定型或积分型）和积分类别（5类积分之一）。如何设计G_p和G_d还缺少研究；

（6）注意各类软约束、硬约束、等关注偏差、外部目标及其期望允许变化范围、外部设定值等，它们是外来和自动形成的，并不是可调参数。

以上调参数的方法很有效，但是不能让追求严格结果的学者满意。实际上，一直以来，MPC的主流稳定性研究是通过较大幅度地修改算法完成的^{[28，29，64，86]}，虽然得到了很多稳定性成果，但是并没有最终解决工业MPC的调整问题，满意仅停留在可接受的数学范围内，而不是在工程界。下面，针对学者满意，有时相信有工程前途的“预测控制中的数学问题”，进行简评。

现有的稳定性研究中，多采用目标函数的最优值做Lyapunov函数，这对分层优化的算法是很难奏效的。实际上，如果是以递阶结构的工业MPC为解决问题的基准，现有的MPC稳定性研究成果是在不同级别的简化下近似研究的成果。让我们针对由“RTO+双层结构MPC+被控系统模型”组成的架构，列出如表9-1所示的复杂性。

以表9-1为基础，可以将MPC的研究分成0～12共13个级别。级别越高，级别数越低；每增加一个复杂性，级别高一级，级别数减一；每减少一个复杂性，级别低一级，级别数加一。比如，具有所有12个复杂性的研究为第0级，而不具有任何一个复杂性的研究为第12级。目前，针对不含RTO、结构固定、单层的研究是主流，而含RTO、变结构、递阶这3个复杂性（尤其是前2个复杂性）的稳定性研究成果很少；考虑双层的稳定性研究时，基本上假设SSTC是无约束的^[21，35]。针对其他9个复杂性的各种组合，已经得到了系列的稳定性结果（SCI论文数以千计），可大致总结如下：(www.xing528.com)

表9-1 递阶结构工业MPC的复杂性列表

•状态可测、调节问题的稳定性研究有成熟的理论体系^{[28，29，64，86]}；

•输出反馈（状态不可测）、无模型参数误差、调节问题的稳定性研究有成熟的理论体系^[27]；

•输出反馈、有模型参数误差、调节问题的稳定性研究已经得到了一些结果^[6，7]；

•用于特别非线性模型（如非完整动力学模型）的进展很少^[13]；

•自适应（未包含在12个复杂性中的）控制的研究成果极少^[10]；

•跟踪控制仅有少量成果^[21]。

对这些分级、近似的研究，本书的主要观点如下：

•级别的高低不是判断水平和贡献的准绳，作为应用数学的分支，稳定性研究的正确性和原创性是判断水平的关键。

•这是以递阶结构的工业MPC为基准的分级，相当于默认了“递阶结构的工业MPC为研究的目标和归宿”这样的公理。但可以允许不相容的另外一个公理站脚，即“解决稳定性等控制理论核心问题是目标和归宿”——这个公理甚至可以质问：“不能解决稳定性的递阶结构的工业MPC是否足够科学？”

•完整地用学术方法阐述MPC的实际应用，涉及所有的控制理论和相关工程知识，并不是某一种或几种MPC学术理论可以概括的。

•MPC稳定性研究的实质，是各类研究人员的全体在数量不同的复杂性上进行的组合式、折中式的论证，是以升级、降级等方式所做的改进式、精细化探索，其终极目标是针对所有复杂性的完备化的稳定性理论体系。

《聊斋志异》中第一卷第一篇《考城隍》中的考题是“一人二人，有心无心”。针对上述分级近似的研究论著，如果出现错误或无创新，则不管源于何因，都会将负能量输送给陌生读者。如果你是这门学问的新手，你一般会问这样的问题：“我现在所献身的这门学问，一般的研究结果究竟在多大程度上是有用的？它的哪些东西是本质的，哪些则只是发展中的偶然的东西？我为什么要研究这门学问，以及这门学问能给我带来什么？”可惜本书还不能准确地回答这些问题，毕竟预测控制稳定性研究的前景尚有很多不可预测的地方。MPC的稳定性研究成果领先其工程应用15～30年，而双层结构MPC的工程应用领先其稳定性理论15～30年，因此在MPC的研究中，理论与实践是各领风骚20年，莫以吾丑对尔美的状况。研究MPC应善于从大趋势中寻找小趋势，从当前发展的大环境中寻找契机。尚可负阴抱阳，面对应用界阴为数学问题、阳为工程算法，面对数学界阴为应用价值、阳为数学问题，这样做才能达到对MPC的融会贯通、之乎者也。