以上无静差控制的结论可以推广到第4~6章更一般的控制器和SSTC的情况。在第4章4.1~4.3节,曾得到如下控制律:
如果系统达到稳态时,输入/输出幅值约束不起作用(即输入/输出没有“卡边”),则得到
其中,Γ=[I,I,…,I]T。注意当存在约束“卡边”时没有以上的解析解 。当
。当 列满秩时,得到
列满秩时,得到
yss(∞)=yol(∞|∞) (9-29)
回顾反馈校正量的计算方法,即e(k+i|k)= ′(k),其中,
′(k),其中,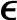 ′(k)为
′(k)为 (k)经过一阶惯性滤波或者有限时域平均得到的,
(k)经过一阶惯性滤波或者有限时域平均得到的, (k)=y(k)-yol(k|k)。因此,e(∞+i|∞)=
(k)=y(k)-yol(k|k)。因此,e(∞+i|∞)= ′(∞)=
′(∞)= (∞)=y(∞)-yol(∞|∞)。采用该校正量校正的结果为YolN(∞|∞)=YolN(∞-1|∞-1)+Γ
(∞)=y(∞)-yol(∞|∞)。采用该校正量校正的结果为YolN(∞|∞)=YolN(∞-1|∞-1)+Γ (∞)=YolN(∞-1|∞-1)+Γ[y(∞)-yol(∞|∞)]。注意到yol(∞+i|∞)=yol(∞|∞)=yol(∞+i|∞-1),因此(https://www.xing528.com)
(∞)=YolN(∞-1|∞-1)+Γ[y(∞)-yol(∞|∞)]。注意到yol(∞+i|∞)=yol(∞|∞)=yol(∞+i|∞-1),因此(https://www.xing528.com)
y(∞)=yol(∞|∞) (9-30)
即e(∞+i|∞)=0。综合式(9-29)~式(9-30)得到yss(∞)=y(∞),即实现了无静差控制。
第4.4节进一步引入了误差校正矩阵H。在以上的分析中,若由H代替Γ,则关于无静差控制的结论仍然成立,不管是否采用一阶惯性滤波,而且H有无穷多种取法。对积分CV, ′(k)被分成两部分,一部分对开环预测的校正为恒值形式;另一部分对开环预测的校正为斜坡形式。当含有积分CV时(见第5章),类似的无静差控制的结论也是成立的。
′(k)被分成两部分,一部分对开环预测的校正为恒值形式;另一部分对开环预测的校正为斜坡形式。当含有积分CV时(见第5章),类似的无静差控制的结论也是成立的。
注意所有前面的对双层结构MPC的无静差特性的分析不依赖于所采用的模型是否准确。在得到以上无静差结论的预设条件下,确实不再需要模型的准确性,但是模型不准确会破坏这些预设条件。因此,对实际运行的双层结构MPC,模型的准确性对动态稳定性和无静差特性都是有最重要的影响的。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




