本节中,将采用的目标函数与第6章不同,但这并不是证明无静差结论的关键,即采用第6章的目标函数时,同样能得到无静差控制的结论。另外,本节将不采用第6章的预镇定控制律,但是和第6章一样,都可以用于不稳定模型。
本节内容参考了参考文献[31,41],并有所改动。在采样时刻k,已知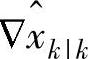 和
和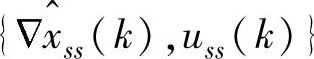 ,采用如下的方法计算当前控制输入:
,采用如下的方法计算当前控制输入:
uk|k=v*k|k+uss(k) (9-14)
其中,v*k|k是如下QP问题的解:
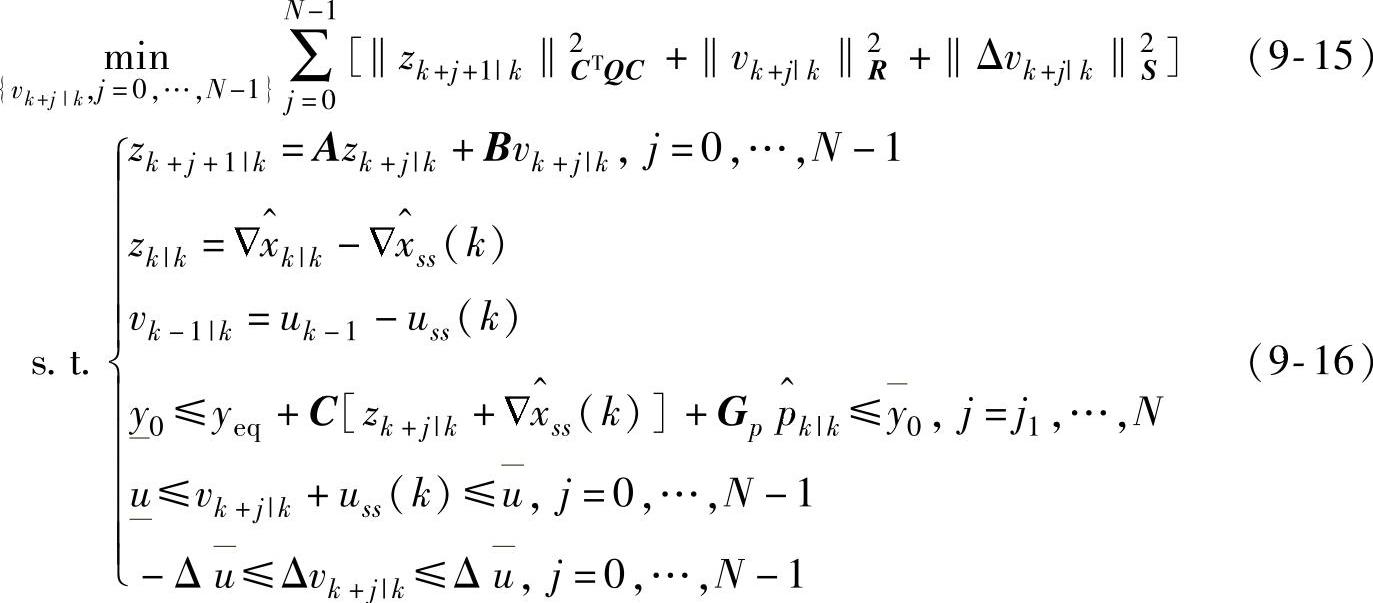
加权矩阵Q、R、S保证线性二次型调节器对应的Riccati迭代可行。
引理9.2如果增广模型的估计器(9-4)是稳定的,且扰动状态的个数与输出的个数相等,即nd+np=ny,则滤波增益L2=[LTd,LTp]T满秩。
证明:由于nd+np=ny,L2是方阵,且可表示为Jordan标准型L2=VJV-1,其中J是上三角阵。使用反证法。假设L2是不满秩的,这说明J的某个特征值为零。假设J中的特征值已经被排序使其零特征值位于对角线的底部。由稳态Kalman滤波的稳定性可推知矩阵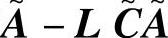 是稳定的。记
是稳定的。记
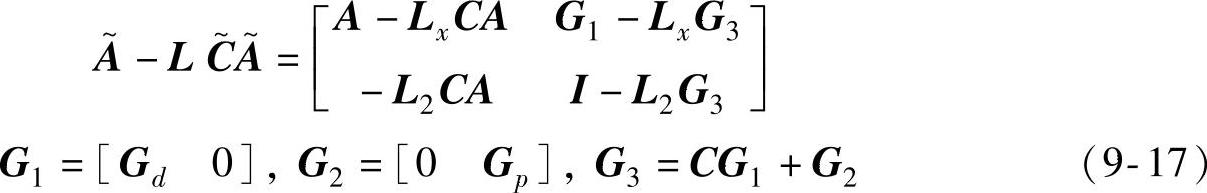
定义
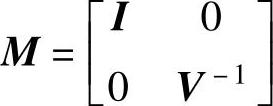
 与如下的相似矩阵具有相同的特征值:
与如下的相似矩阵具有相同的特征值:
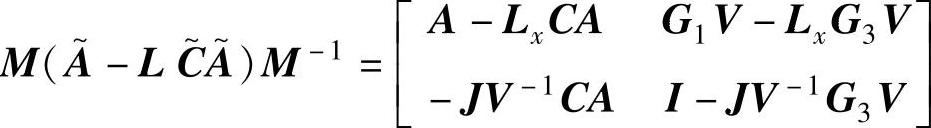
由于J是上三角矩阵且零特征值位于对角线的底部,所以J的最底部的一行全为零。矩阵[-JV-1CAI-JV-1G3V]的最底部一行为[0…0 1],这意味着估计器有一个特征值为1,所以不稳定。显然,这与估计器的稳定假设矛盾,因此L2必须是满秩的。
证毕
定理9.3 考虑输出反馈预测控制,目标函数为式(9-15),约束条件为式(9-16),状态估计器为式(9-4),SSTC描述为目标跟踪问题式(9-6)~式(9-9)或式(9-11)。记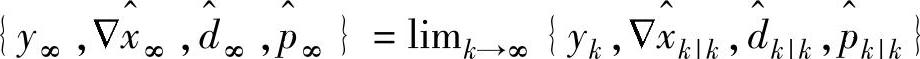 。该控制器在如下的条件下实现无静差控制:
。该控制器在如下的条件下实现无静差控制:
(i)闭环系统是渐近稳定的,在稳态时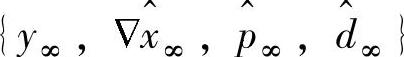 恒定不变;
恒定不变;
(ii)式(9-1)所示的过程模型可镇定且可检测;
(iii)nd+np=ny;
(iv)式(9-2)所示的增广模型是可检测的;
(v)输入和输出的不等式约束在稳态不起作用。条件(i)需要闭环系统实际到达稳态,其中也包括优化问题时时可行。条件(ii)使得稳定的控制器、可检测的增广模型、唯一确定的 成为可能。根据第6章有关结论,条件(iii)确保了可检测增广模型的存在性。条件(iv)确保了稳定的观测器可以被构造。条件(v)确保稳态时可以采用由无约束控制器确定的控制输入。
成为可能。根据第6章有关结论,条件(iii)确保了可检测增广模型的存在性。条件(iv)确保了稳定的观测器可以被构造。条件(v)确保稳态时可以采用由无约束控制器确定的控制输入。
证明:由式(9-2)的增广模型的状态估计器,产生如下的稳态估计:
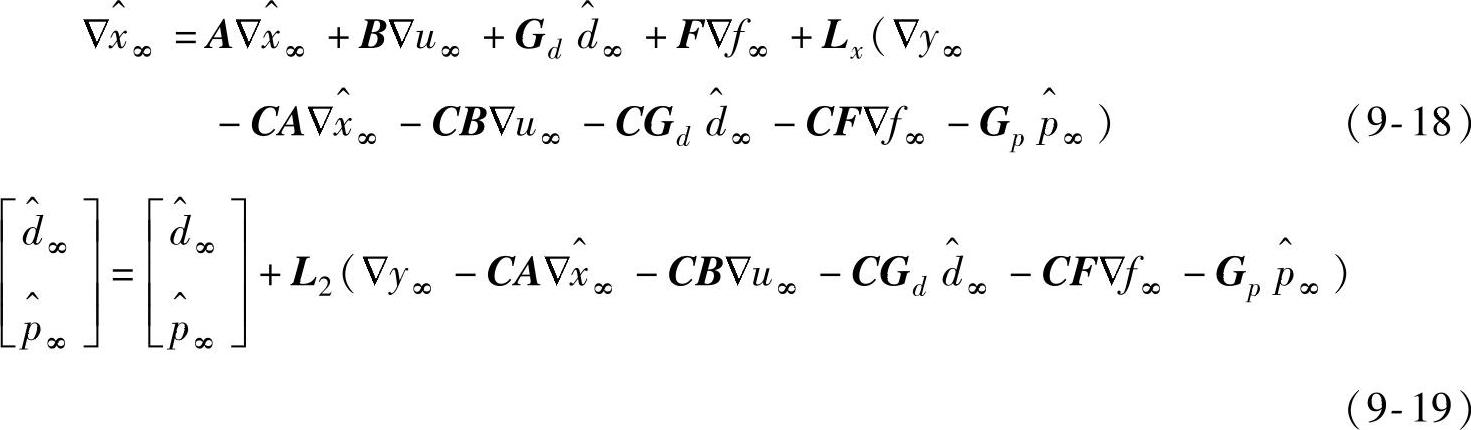
由于闭环系统是渐近稳定的(说明增广状态估计器也是稳定的)和nd+np=ny,由引理9.2可知L2是满秩的。根据式(9-18)和式(9-19),满秩的L2分别意味着
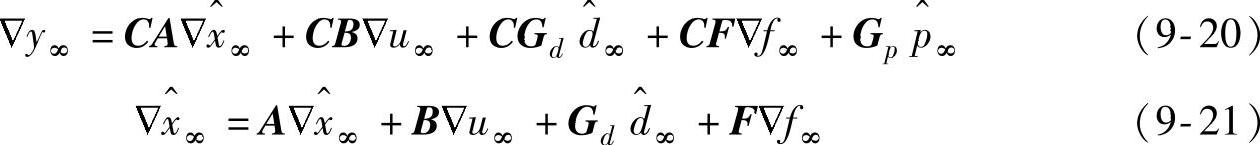
进一步将式(9-21)带入式(9-20)得到

由于条件(ii),SSTC存在唯一解。因此,约束条件式(9-7)必须得到满足,即
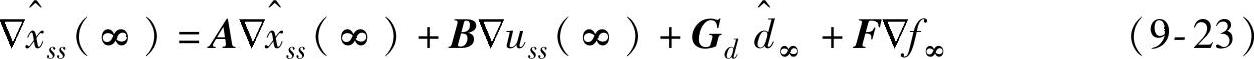
式(9-21)减式(9-23)得(https://www.xing528.com)
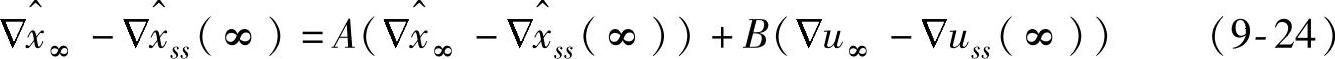
由于过程模型式(9-1)是可镇定的和条件(i),控制输入可以通过有限时域无约束线性二次型调节器(Linear Quadratic Regulator,LQR)方法进行计算,即
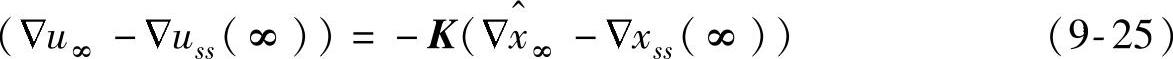
其中,K为增益矩阵。将式(9-25)代入式(9-24)得到
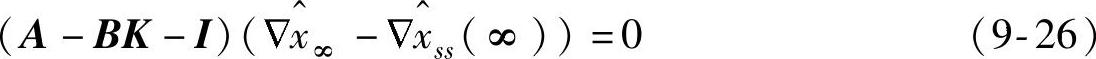
反馈增益的渐近稳定性意味着矩阵(A-BK)是稳定的,因此式(9-26)必然导致 。由式(9-5)可知,可达的输出目标为
。由式(9-5)可知,可达的输出目标为
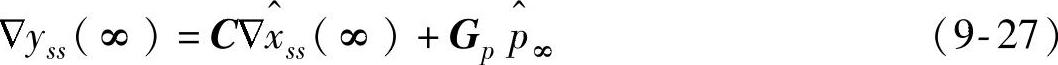
式(9-22)减式(9-27)得
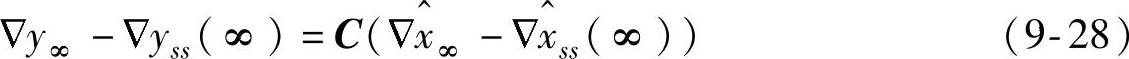
这意味着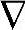 y∞=
y∞=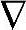 yss(∞)。
yss(∞)。
证毕
在这一无静差控制的结论中,条件(i)的满足是需要深入研究的问题,在各种复杂情况下尚且是未解决的公开问题。条件(v)要求各种不等式约束(输入输出幅值)在稳态时不起作用,对一般的SSTC而言也不容易做到,故如何删除(v)是未解决的公开问题。
例9.1采用第3章的重油分馏塔模型,在平衡点附近连续时间传递函数矩阵
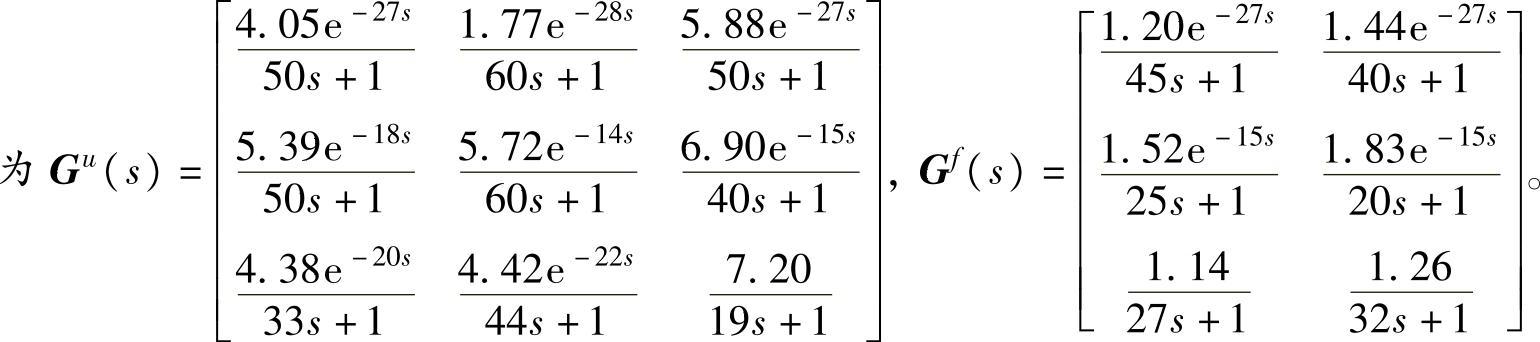
采样周期为4。采用第8章的开环子空间辨识方法得到状态空间模型,nx=20。首先取yeq=0、ueq=0和feq=0。u(-1)=ueq,y(0)=yeq,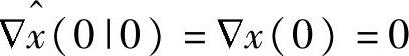 。MV、CV的相关约束如下:
。MV、CV的相关约束如下: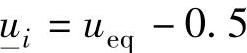 、
、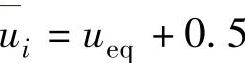 、
、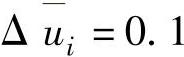 ;
;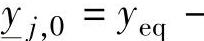
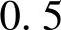 、
、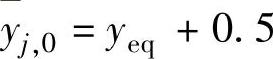 。外部目标yt=yeq+[0.5,-0.5,0.5]T,ut=ueq+[0.5,-0.5,0.5]T。
。外部目标yt=yeq+[0.5,-0.5,0.5]T,ut=ueq+[0.5,-0.5,0.5]T。
取Gd=[I2,0]T,Gp=[1,0,0]T。在SSTC,通过求解优化问题式(9-11)可得到各时刻的稳态目标,各参数选取如下:Qs=I3、Rs=I3、qs=[0.5,0.5,0.5]T。在动态控制部分,取N=10,j1=1,Q=Qs,R=S=Rs,被控对象为Ar=0.8A,Br=0.8B,Cr=0.8C,Fr=0.8F。可测干扰fk在时刻k=158~168和k=228~238发生变化,幅值分别为feq+[0.05,0.05]T和feq-[0.05,0.05]T,其他时间段内fk=feq。通过求解优化问题式(9-15)~式(9-16),并利用式(9-14),可求得MV动态值。控制结果如图9-1所示,MV和CV可无静差地跟踪到相应的稳态目标值。
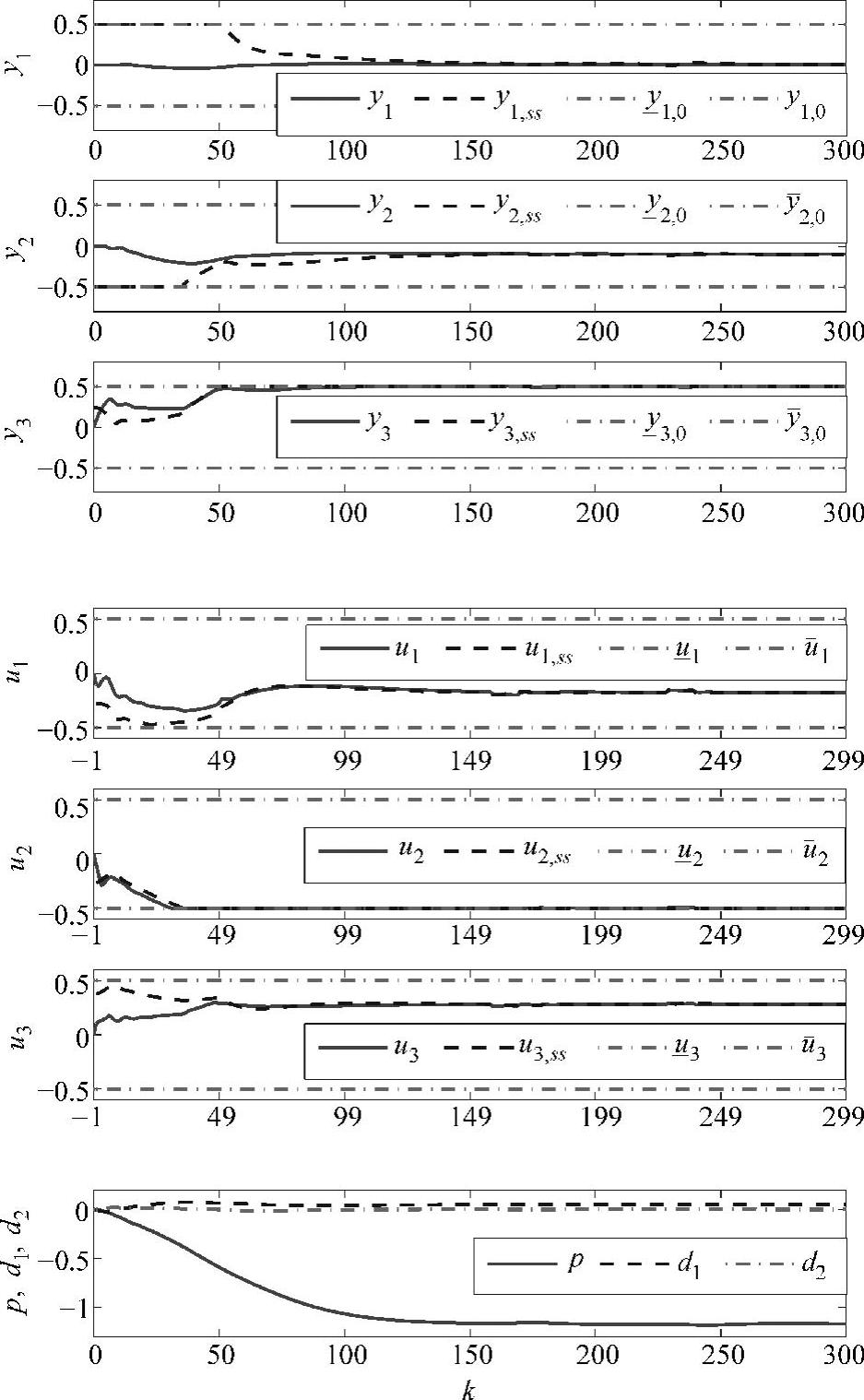
图9-1 控制效果图
如果没有模型失配(即Ar=A、Br=B、Cr=C、Fr=F),且平衡点{x,y,u,f}eq满足
(I-A)xeq=Bueq+Ffeq,yeq=Cxeq
则平衡点的任意移动仅影响仿真中各变量的绝对数值,不影响相对值(曲线形状)。取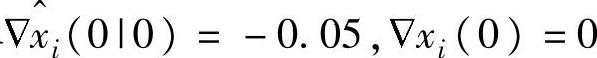 。针对两组平衡点{ui,eq=23,fi,eq=17}和{ui,eq=-123,fi,eq=32},控制结果分别如图9-2和图9-3所示。注意当没有模型失配时,d和p的稳态值为零。
。针对两组平衡点{ui,eq=23,fi,eq=17}和{ui,eq=-123,fi,eq=32},控制结果分别如图9-2和图9-3所示。注意当没有模型失配时,d和p的稳态值为零。
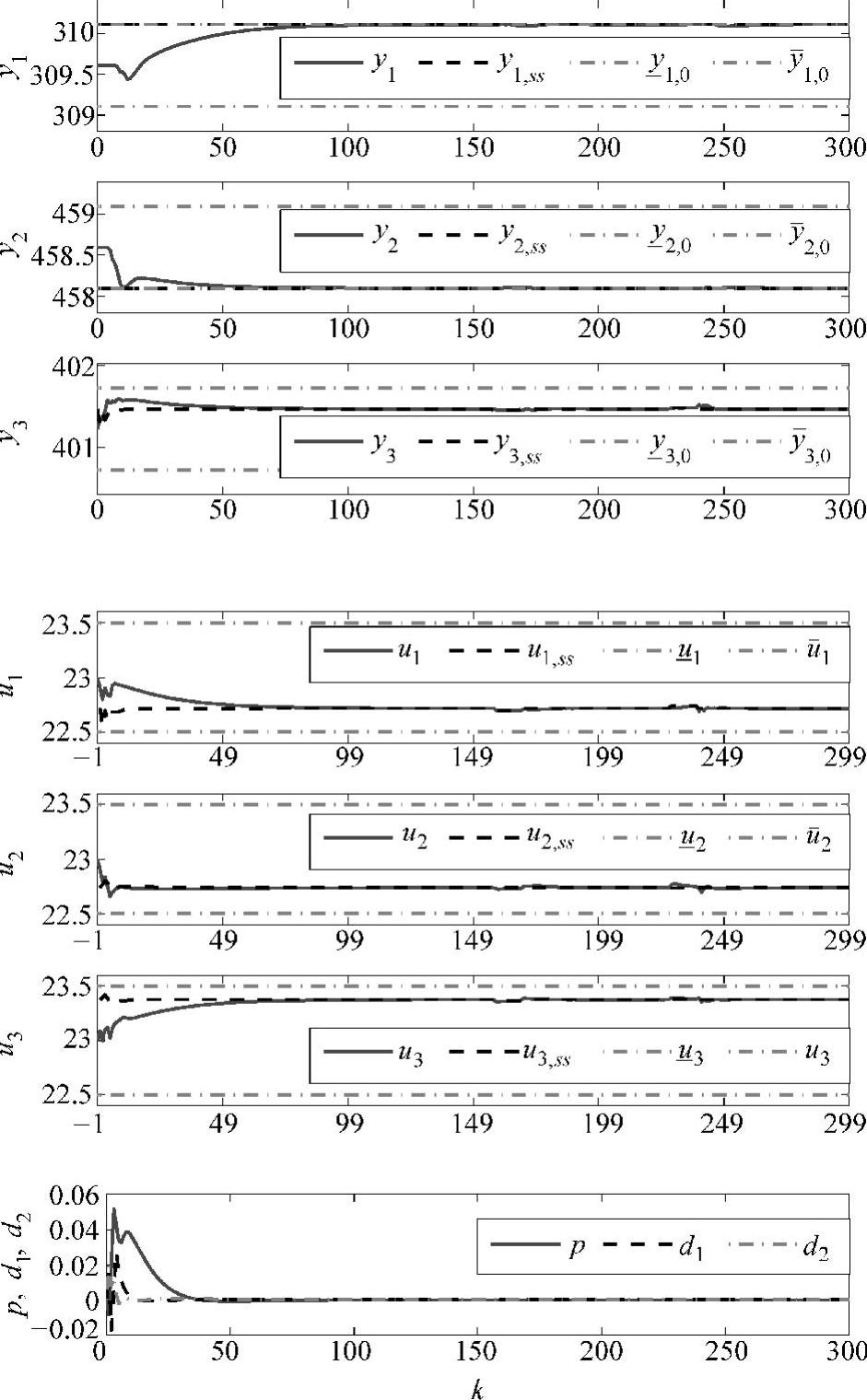
图9-2 控制效果图
注意,取任意其他的平衡点时[不需考虑平衡点是否满足(I-A)xeq=Bueq+Ffeq和yeq=Cxeq],本章算法仍然可用。取ui,eq=0.1,fi,eq=0.09,xi,eq=ξi(I-A)-1(Bueq+Ffeq)-0.1,yi,eq=ξiCxeq+0.05,其中,ξi为单位阵的第i行。取外部目标yt=yeq+[0.5,-0.2,0.4]T,ut=ueq+[0.5,-0.5,0.5]T,以及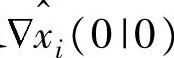 =-0.05,
=-0.05, xi(0)=0.05。被控对象为Ar=0.95A,Br=0.95B,Cr=0.95C,Fr=0.95F。其他参数同前。控制结果如图9-4所示。
xi(0)=0.05。被控对象为Ar=0.95A,Br=0.95B,Cr=0.95C,Fr=0.95F。其他参数同前。控制结果如图9-4所示。
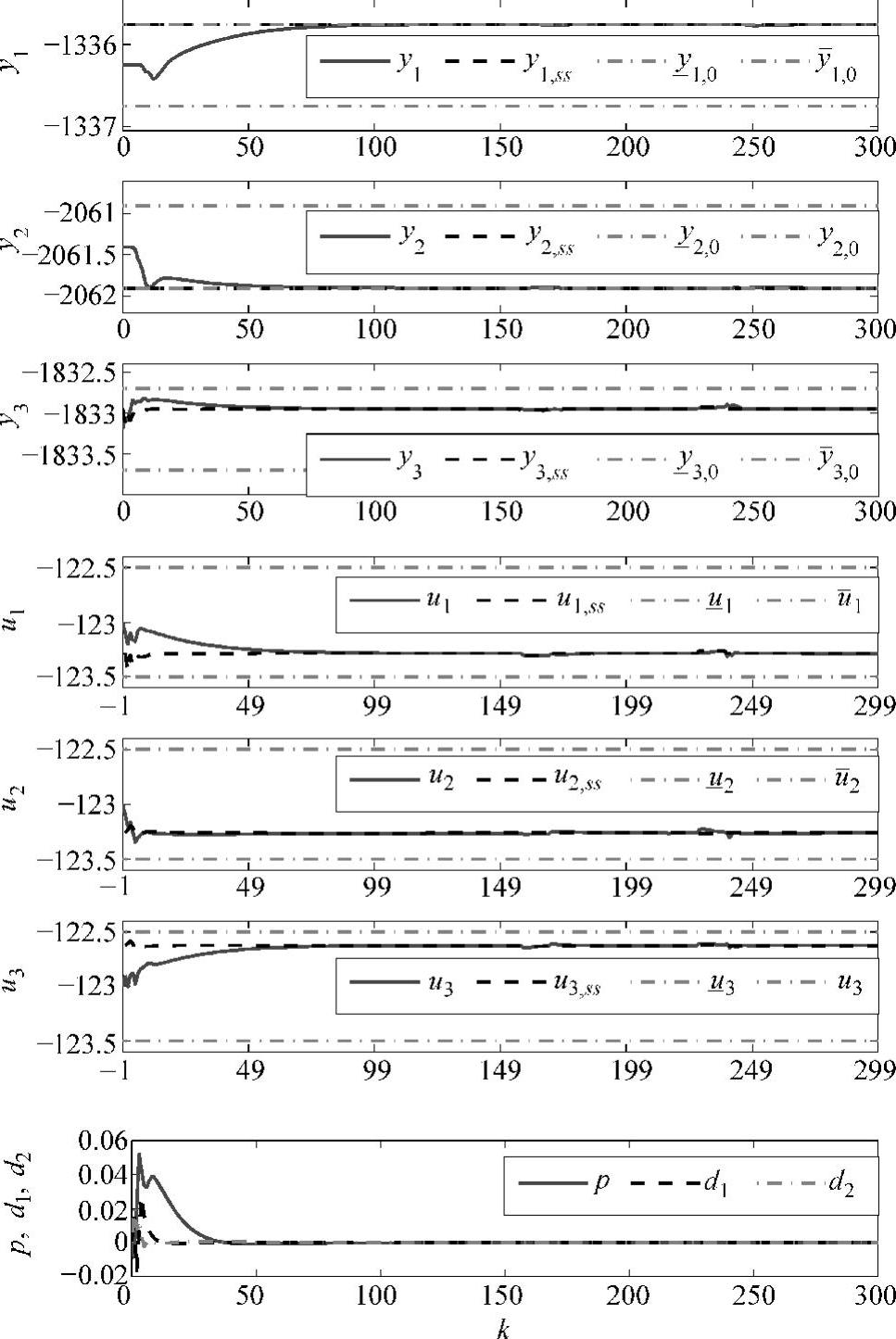
图9-3 控制效果图
本章这两节介绍的双层结构MPC中,-Bueq+F f(k)总是和
f(k)总是和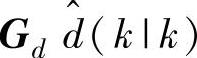 同时出现,而yeq总是和
同时出现,而yeq总是和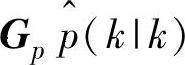 同时出现。因此,{y,u,f}eq不需准确知道,甚至可以省略。当然,更准确地利用{y,u,f}eq一般会得到更好的控制效果。用
同时出现。因此,{y,u,f}eq不需准确知道,甚至可以省略。当然,更准确地利用{y,u,f}eq一般会得到更好的控制效果。用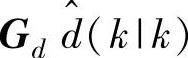 和
和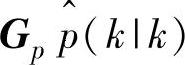 包含稳态工作点将影响控制效果。
包含稳态工作点将影响控制效果。
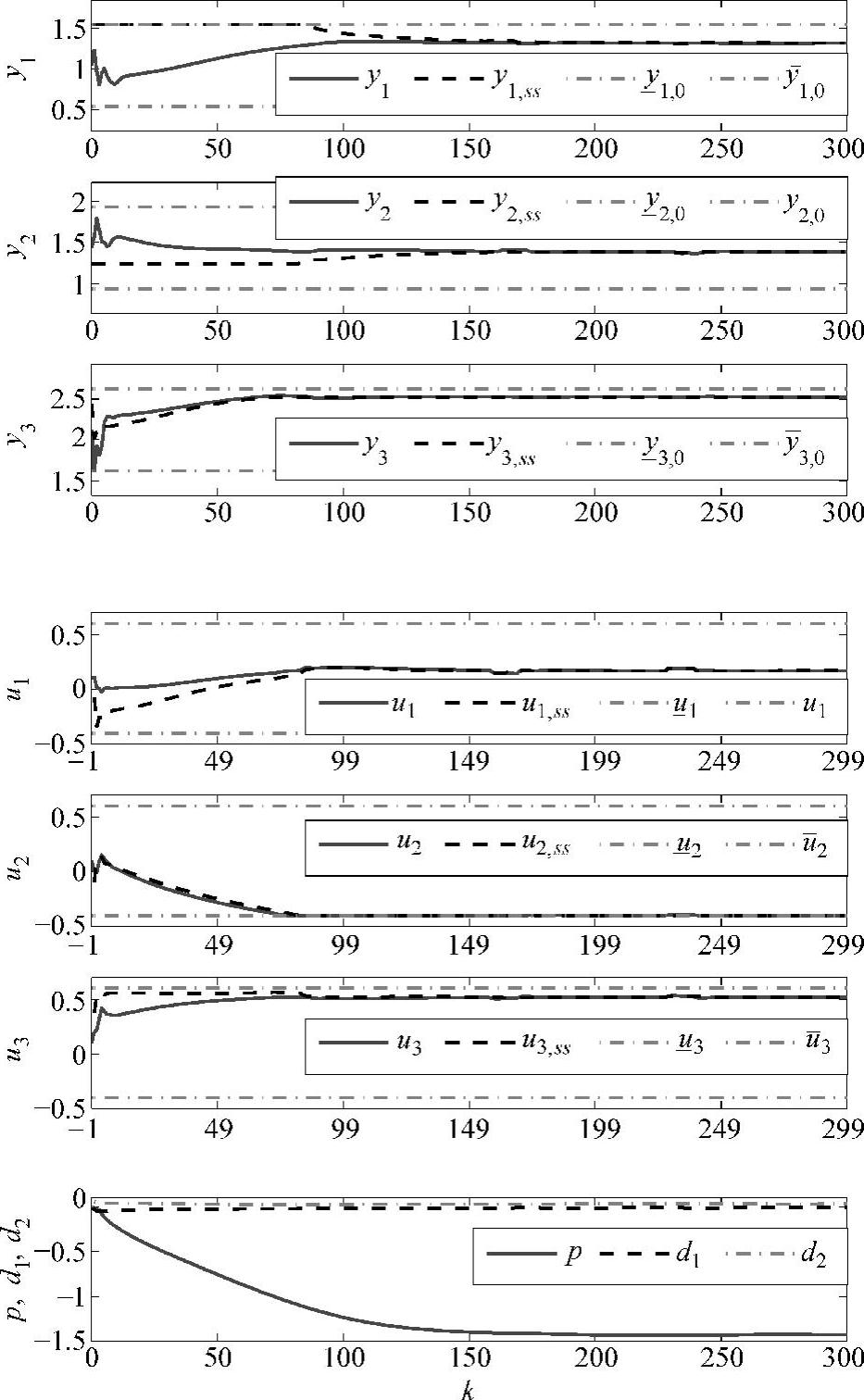
图9-4 控制效果图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




