基于状态空间模型的目标跟踪优化方案

考虑第6章的线性时不变离散模型

其中，输出，控制输入，状态，可测干扰。假设（A，B）为可镇定的，（C，A）为可检测的。模型（9-1）是对系统的近似描述。为了处理不可测干扰、建模误差等，采用带有干扰的状态空间模型描述：

其中，增广的状态变量和系统矩阵为

对式（9-2）～式（9-3）所示的增广模型，增广状态的估计可使用如下方法得到：

状态滤波增益L被分解为过程模型状态滤波增益L_x、状态扰动滤波增益L_d以及输出扰动滤波增益L_p。

基于式（9-4），稳态目标值满足下面的关系式：

其中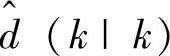，和由式（9-4）给出。记y_t为ETCV，u_t为ETMV。与第6章不同的是，所有的MV和CV都有外部目标。

（1）所有外部目标有相同的重要性的情形内容参考参考文献[31]，并有所改动。稳态目标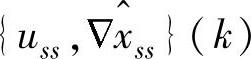可以通过求解如下的二次规划问题来确定：

其中，R_s和Q_s为对称正定矩阵，y_ss（k）实际由代替。该优化问题仅相当于多优先级SSTC中某优先级的优化，但该优先级是“ET的跟踪”、所有MV和CV都有理想值且处于同一个优先级。式（9-7）是式（9-5）的第一个式子。如果式（9-8）～式（9-9）不是积极的（即不起作用），则求解问题式（9-6）～式（9-9）等价地简化为求解问题式（9-6）～式（9-7）。

若较大，使得约束条件式（9-9）的存在造成问题式（9-6）～式（9-9）不可行，则可以采用对式（9-9）软化的方法，即引入松弛变量，见第6章。

（2）被控变量外部目标的重要性高于操作变量外部目标的情形

内容参考参考文献[41]，并有所改动。假设y_t的实现比u_t更重要。当n_u＝n_y，模型具有可逆的稳态增益矩阵（至少要求系统不含积分环节）时，无约束目标跟踪问题的解可直接由稳态增益矩阵获得。但是，多数时候n_u≠n_y，有时包含积分环节、一般存在稳态目标的不等式约束，因此目标跟踪问题更一般的是被描述成为一个数学规划问题。当n_u＞n_y时，经常多种u_ss（k）可产生同一个y_t，对此可构造一个QP问题来求得最佳的u_ss（k）。当n_u＜n_y时，经常不存在u_ss（k）的组合确保y_t的跟踪，对此可设计优化问题使y_ss（k）在最小二乘意义下尽可能地接近y_t。

与其构造以上两种优化问题，不如采用统一的优化问题应对各种情况。设计输出目标的软约束为(www.xing528.com)

这样，就可将目标跟踪问题描述为如下的QP问题：

其中，q_s是由非负元素组成的向量，y_ss（k）实际由代替。该优化问题不能相当于第6章某个优先级的优化。由于R_s和Q_s是对称正定的，根据QP的特点知ε（k）和u_ss（k）将被唯一确定。

目标函数中的线性项q^T_sε（k）和二次项ε（k）^TQ_sε（k）用来惩罚软约束的调整量。如果q_s取值足够大，软约束将得到最低限度的调整。但确保该最低限度的q_s的下界不容易事先准确计算得到。实际中，很少要求软约束必须得到最低限度的调整，根据一定的经验近似选定q_s即可。从软约束得到最低限度的调整的角度看，中括号内的二次惩罚项似乎是多余的，但事实上该二次项不仅增加更多的可调参数，而且对确保解u^*_ss（k）的唯一性也是必要的。

在以上两种情形中，由于（A，B）是可镇定的，则矩阵[（I-A）-B]满秩。根据式（9-7），这是一个保证可行解存在的充分条件，如以下结论所述。

引理9.1 由于（A，B）是可镇定的，故不含约束式（9-8）～式（9-9）的以上两种情形中的目标跟踪问题有可行解。

对任一ε^*（k），存在唯一、非负的{ε+，ε_-}^*（k）使得ε^*（k）＝ε^*+（k）+ε^*_-（k）和y^*_ss（k）＝y_t+ε^*₊（k）-ε^*_-（k）。当QP可行时，得到唯一的{u_ss，ε}^*（k）。

由式（9-5）得到

显然，当QP可行时，由式（9-12）确定唯一的的充要条件是满秩。由第6章的Hautus条件知道，（C，A）的可检测性保证了满秩。总之，由于（C，A）是可检测的，QP可行时，以上两种情形的解是唯一的。如果去掉不等式约束式（9-8）～式（9-9），则可行域一定是非空的，因而（C，A）可检测和（A，B）可镇定保证了目标跟踪问题的解的存在性和唯一性。

考虑{y_t，u_t}都希望被准确跟踪的情况，即状态目标需要满足

由式（9-13）确定唯一的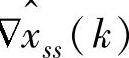的必要条件是满秩。

注解9.1 的非唯一性表示它是无规则跳动的，故若用于动态控制，则会使闭环系统无法稳定。仅从保证QP解的唯一性的角度，（C，A）可检测不是必要条件；在A不含积分模态时，由u_ss（k）唯一得到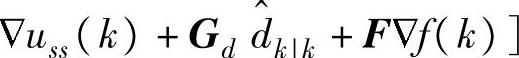，可保证两种情形下解的唯一性。但（C，A）可检测是采用式（9-4）的必要条件。

以上只讨论了目标跟踪问题。相对于第4～6章的SSTC，以上的目标跟踪问题是比较简单的。