基于N4SID方法的闭环子空间辨识技术

任何系统在长期运行后，参数都会发生变化。在不切除现有预测控制器的情况下重新进行辨识，对实际过程的影响较小。对系统进行闭环控制时，整个系统的幅频特性会发生变化，故闭环辨识结果在设计的控制器工作频率段误差也会比较小。

在闭环下采用前面讨论的开环子空间辨识方法会产生有偏的估计，以N4SID方法为例分析如下。在N4SID方法中采用了式（8-74）所示的斜向投影，由于开环状态下的噪声与输入不相关，所以E_f/U_fZ_p≈0。然而对于闭环系统，由于反馈的存在，噪声和输入信号之间是相关的，故E_f/U_fZ_p≈0不再成立，式（8-75）不再成立，即N4SID方法不适用于闭环系统辨识。闭环子空间辨识的首要问题就是研究如何处理输入信号和噪声之间的相关性。

下面介绍基于两步QR分解的闭环子空间辨识，原算法见参考文献[16]。该方法针对的闭环系统的确定性部分如下：

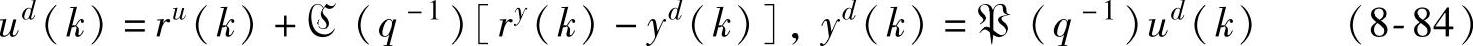
其中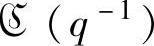，和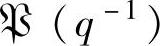分别是控制器和被控对象的传递函数矩阵，r^u（k）和ry（k）为两个参考输入信号，上角标“d”表示确定部分。定义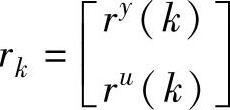，这是辨识中要设计的测试信号。定义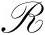＝span{r_k|k＝0，1，…，L}，则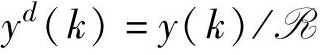、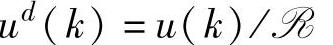（正交投影）。在开环子空间辨识需要的假设下，u_k需要满足的假设替换成r_k需要满足的假设，而假设的形式不变。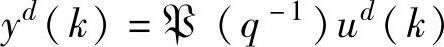的状态空间实现如下：

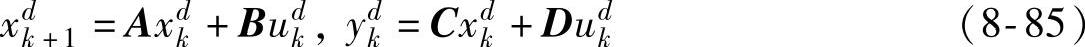
定义

对于数据Hankel矩阵{Y_p，U_p，R_p，Y_f，U_f，R_f}，定义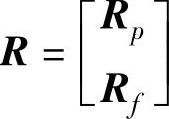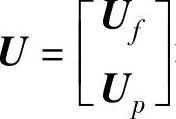，和Y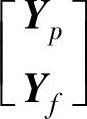＝。在后面的阐述中，用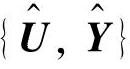表示{U，Y}的确定性部分，与采用上角标“d”是一致的。以下的算法步骤给出的是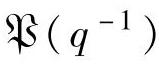的辨识结果[同理可辨识，但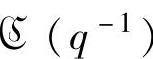可以是已知的]：

（1）计算QR分解

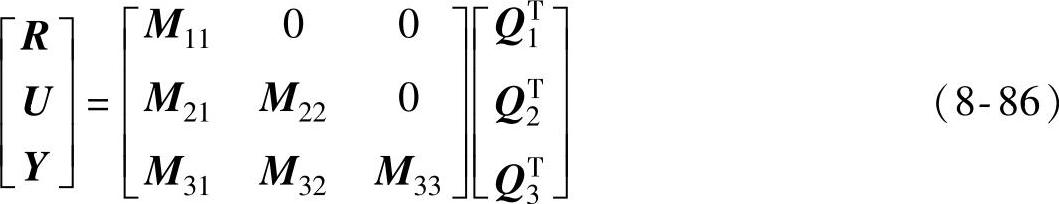
将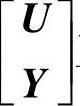正交投影到R的行空间上，由式（8-21）可得

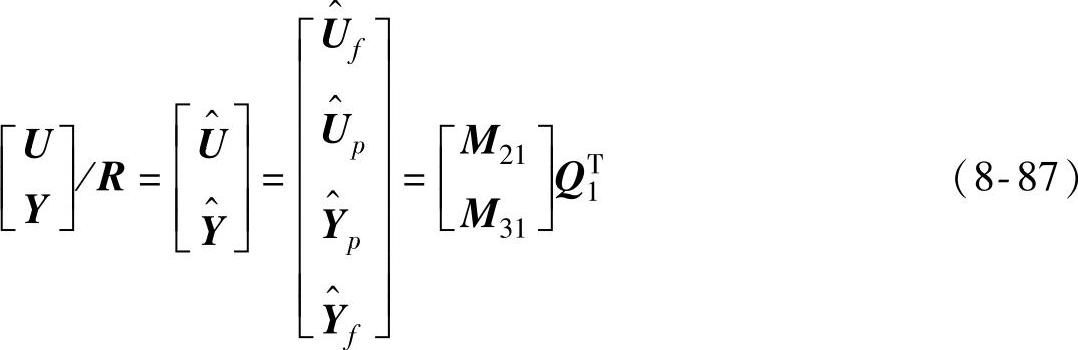
（2）计算确定性部分的QR分解

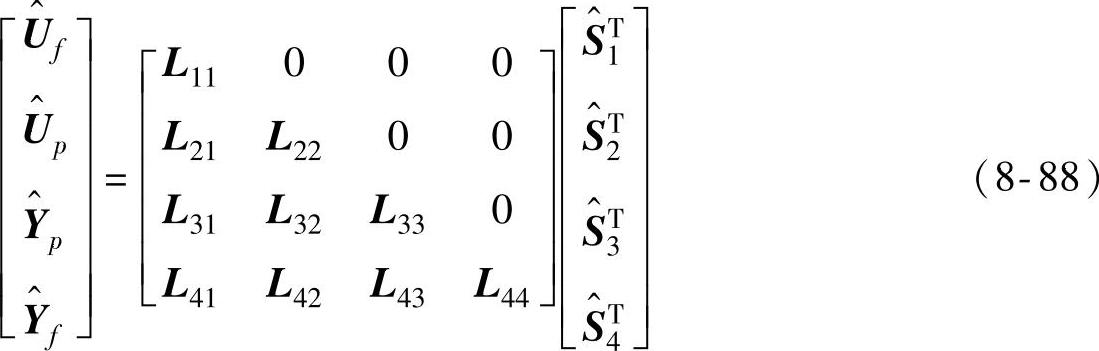
由于Q₁是正交的，也可以直接对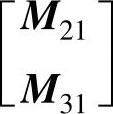进行QR分解以减小计算量。

（3）考虑系统的确定性部分，由于噪声项的估计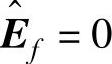，由式（8-48）和式（8-88）可知未来输出

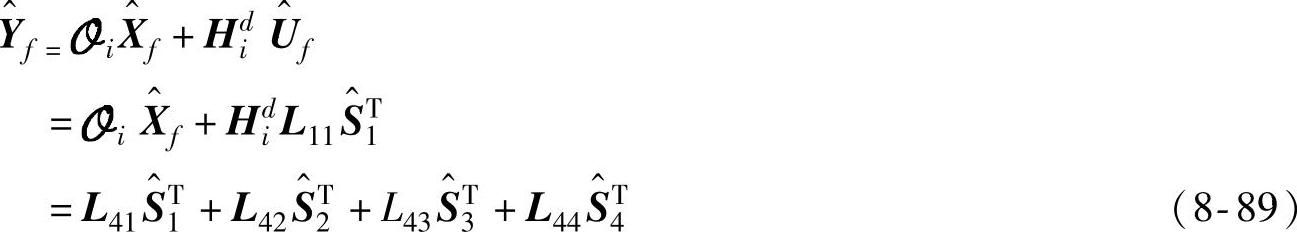(https://www.xing528.com)

对式（8-89）的最后一个等式的两边都右乘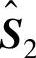，有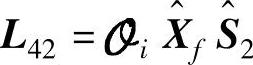。计算L₄₂的SVD分解，有

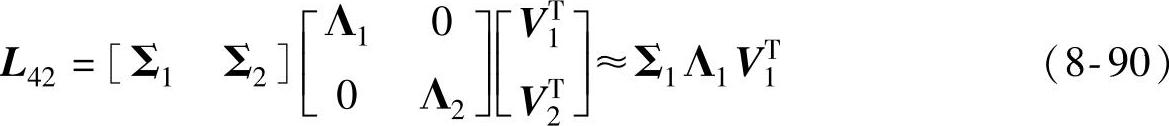
扩展能观性矩阵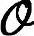_i＝Σ₁Λ^1/2₁，由此可求出系统矩阵A和C。

（4）由于Σ₂^T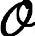_i＝0和Σ^T₂L₄₂＝0，对式（8-89）的最后一个等式左乘Σ^T₂并右乘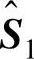，有

Σ^T₂H^d_iL₁₁＝Σ₂^TL₄₁ （8-91）

按照8.3.1节方法可得到系统矩阵B和D。

该方法采用了2步QR分解，由于QR分解是一种正交分解（ORThogonal de-compositions，ORT），故被命名为2ORT（2-stage ORT method）。实际上，该方法的第一步正交分解预处理得到信号的确定性部分后，可以使用前面讲述的任一开环子空间辨识算法辨识系统矩阵。

例8.1 考虑如下系统：

控制器模型为

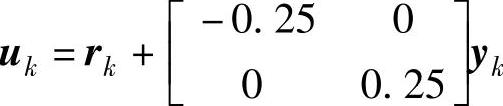
其中，参考输入r_k是转换概率为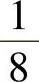、T_min＝T_s的GBN测试信号。产生3000组输入输出数据，Hankel矩阵的行块数i＝8。

采用2ORT法进行辨识，基于辨识模型的输出预测值与真实系统的输出值见图8-17，辨识得到的FSR与真实系统的FSR见图8-18。可见，辨识结果与真实系统能很好地吻合。

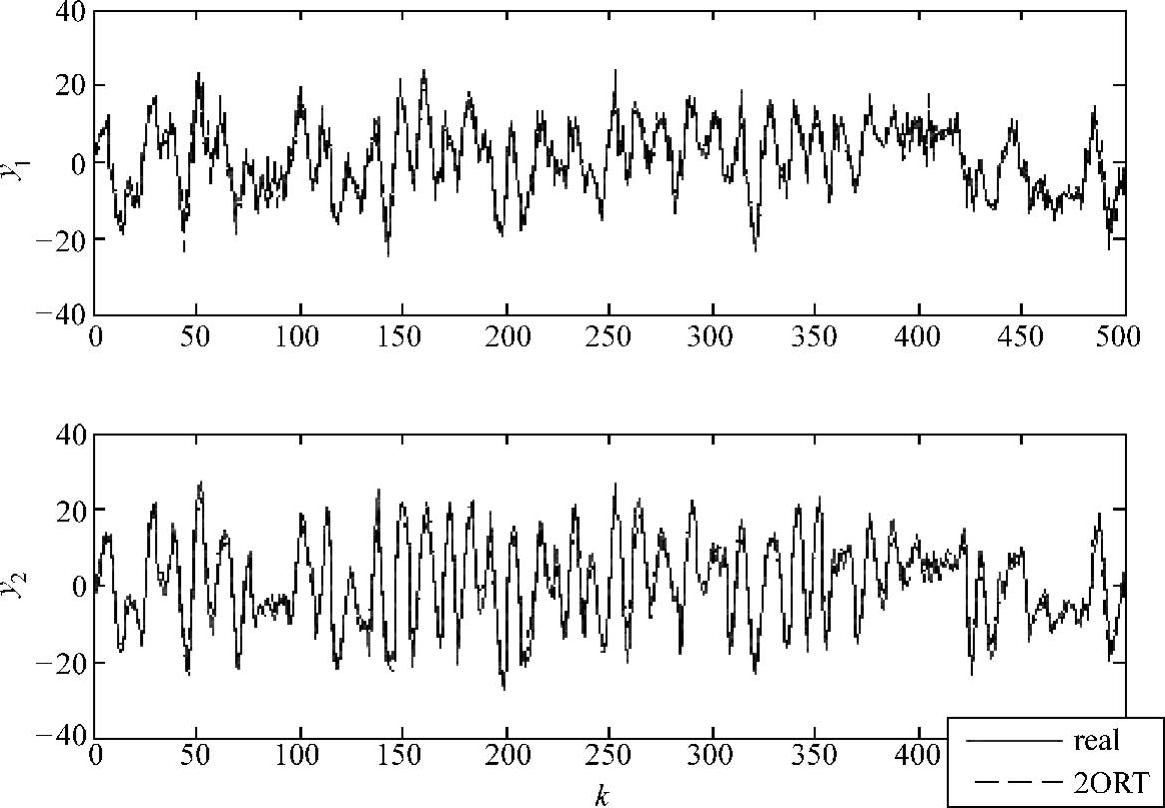
图8-17 基于辨识模型的输出预测值与真实系统的输出值

图8-18 辨识得到的FSR与真实系统的FSR