实验探究三容水箱系统效能

本实验使用浙江天煌科技实业有限公司的THSA-1型过程控制综合自动化控制系统实验平台，其基本构造如图8-12所示。实验时，通过调节电动调节阀的开度改变下水箱的液位高度，显然该控制对象是一个三阶单入单出系统，操作变量MV为调节阀的开度o，被控变量CV为下水箱液位高度h，其中，阀门开度最大范围为[0%，100%]，下水箱液位的最大范围为[0，180]（单位：mm）。

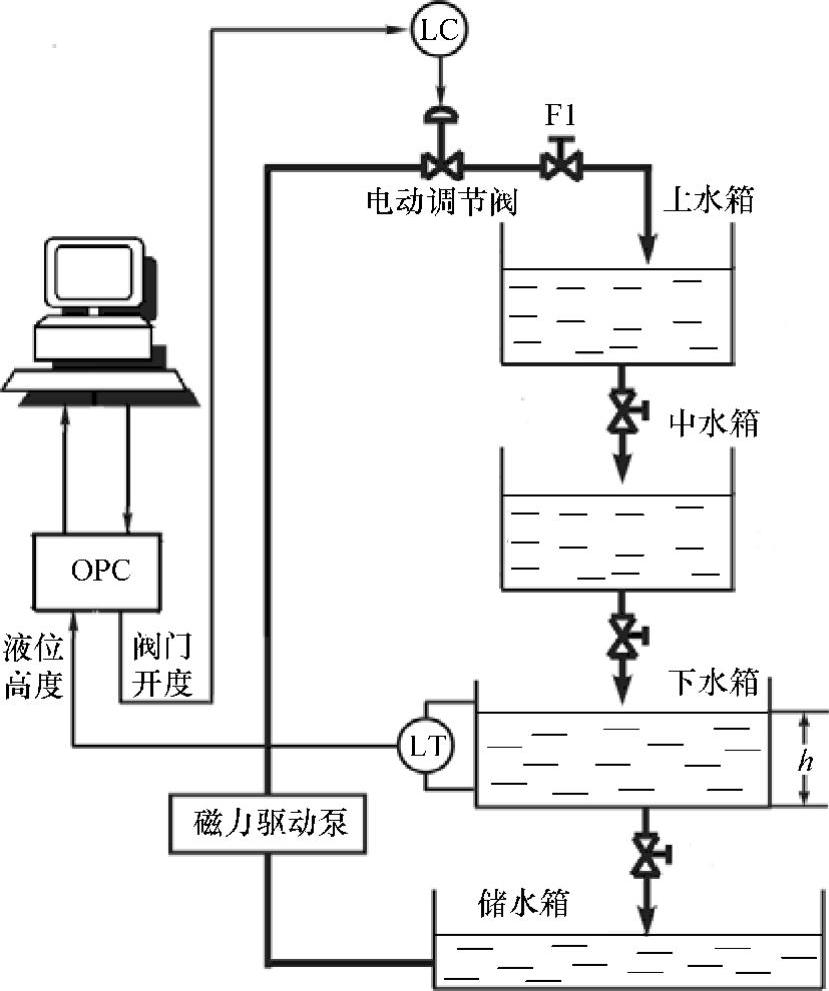
图8-12 三容水箱系统原理图

在辨识实验开始前需要调整系统，确定系统的平衡点作为模型的零点，同时确定MV和CV相较于该零点的变化区间。本实验选取的零点为：阀门开度o＝50%，对应的下水箱液位高度h＝75mm。该实验装置的液位高度和阀门开度等物理量可通过已配置好的组态王软件获得，组态王软件提供了OPC接口可以完成数据的读写，因此我们采用编写的数据采集软件OPCClient读写组态王提供的，实验所需的OPC数据项，包括读液位高度h和写调节阀开度o。首先对系统进行预测试，得到了系统的在达到98%稳态时的响应时间约为1800s。选择采样周期T_s＝40s。

取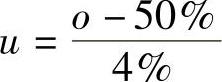，y＝h-75。这样，u＝0对应o＝50%，y＝0mm对应h＝75mm。下面的叙述都是针对u和y。采用幅值a＝1的GBN信号进行测试，T_min＝T_s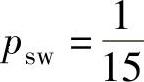，，故平均转换时间为600s。采用上节介绍的三种子空间辨识算法，选取Hankel矩阵行数i＝10，其奇异值直方图分布如图8-13所示（三种方法相差无几，故只给出对应于MOESP的结果），根据先验知识并结合奇异值分布，选取系统阶次n_x＝3。辨识得到的模型参数如下所示：

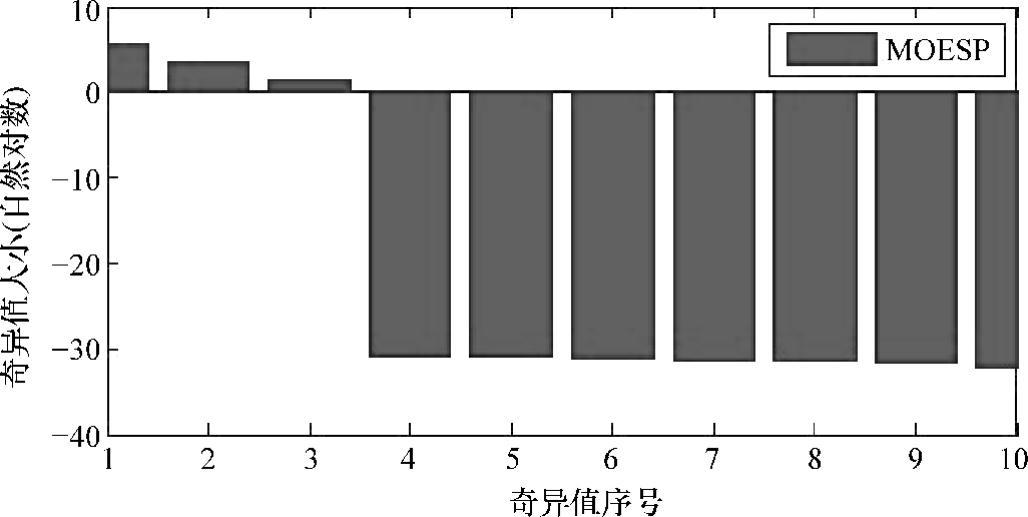
图8-13 奇异值分布直方图（三容水箱）

辨识模型的单位阶跃响应曲线如图8-14所示，其中，稳态增益为60.66。基于模型的输出预测值与输出量测值如图8-15所示，从该图8-15可知，辨识模型准确地反应了系统的动态特性（中高频段），但稳态部分（低频段）有一定误差，此问题可通过增大GBN信号平均转换时间和增加数据采集个数得到解决。

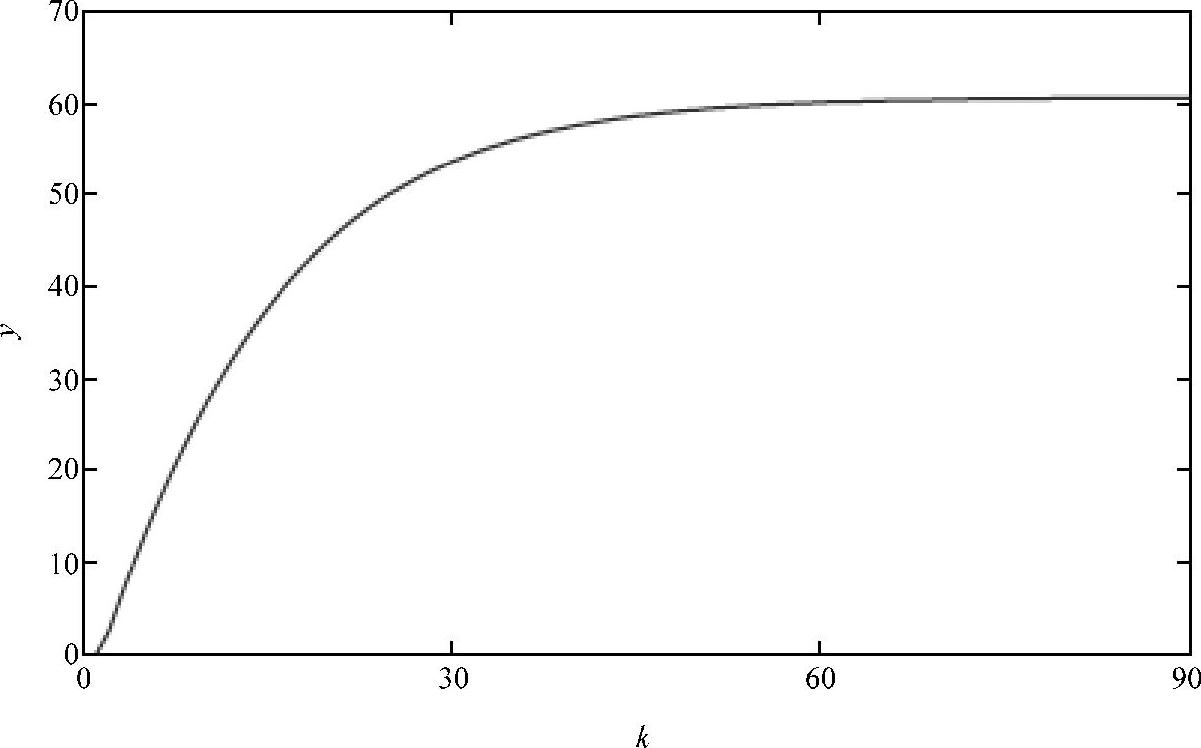
图8-14 辨识模型的单位阶跃响应曲线

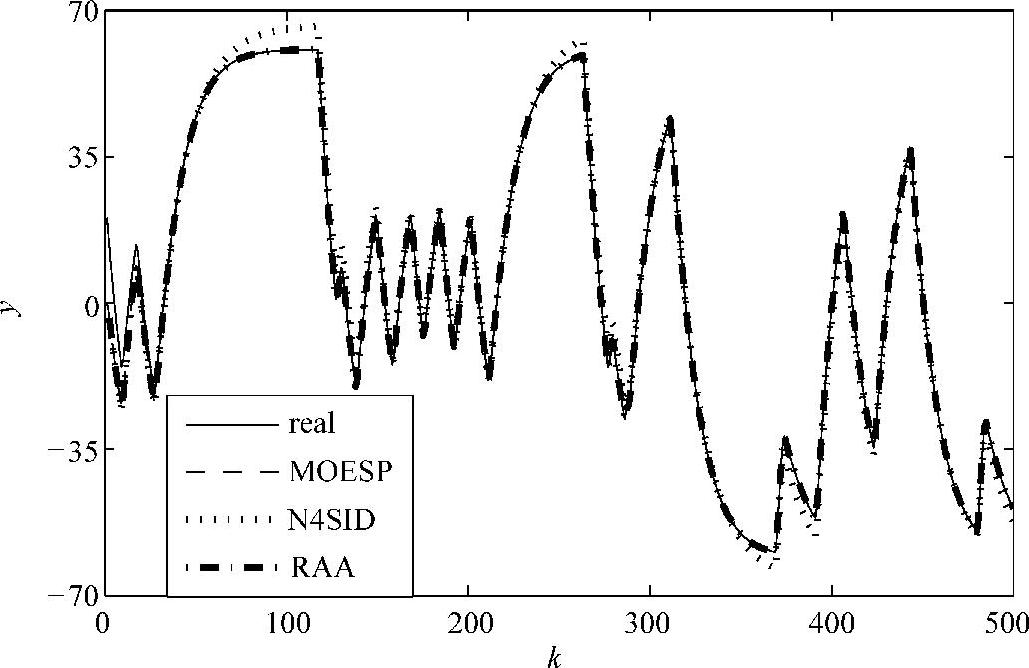
图8-15 输出量测值与预测值的对比(www.xing528.com)

采用第4章的双层MPC算法，重复参考文献[71]中的实验情形。共设计a、b、c、d四组实验，SSTC参数设置见表8-3。开环预测的滤波系数α＝1（即不滤波）。各优先级具体优化问题如下：优先级1：

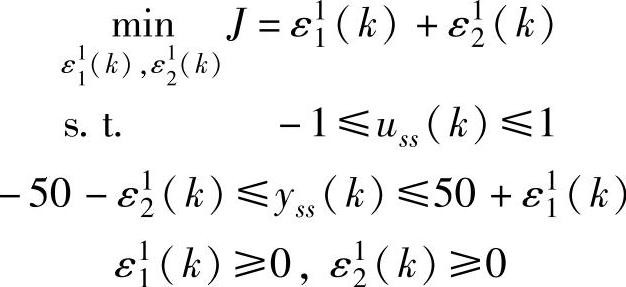
优先级2：

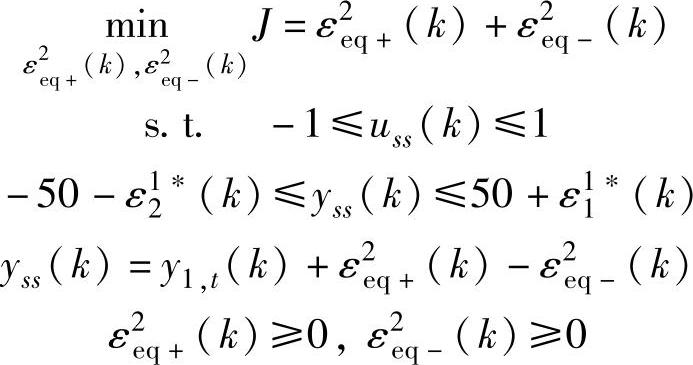
在经济优化中，u_ss（k）直接由y_ss（k）反算得到，不需要设置h和J_min。

在动态控制模块中，选择预测时域P＝15，控制时域M＝4，Λ＝1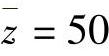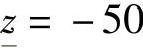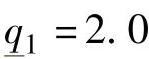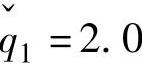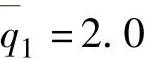，，，，，；将∣u（k）∣≤10和∣y（k）∣≤50作为硬约束，没有控制作用增量约束。输出的期望目标在k＝99、k＝199和k＝229时刻在线切换（四组实验中只有期望目标有区别，其他各个参数的设置不变）。控制结果见图8-16，该图8-16表明，CV可以完全跟踪上稳态目标值的变化。

表8-3 三容水箱实验多优先级SSTC参数选取

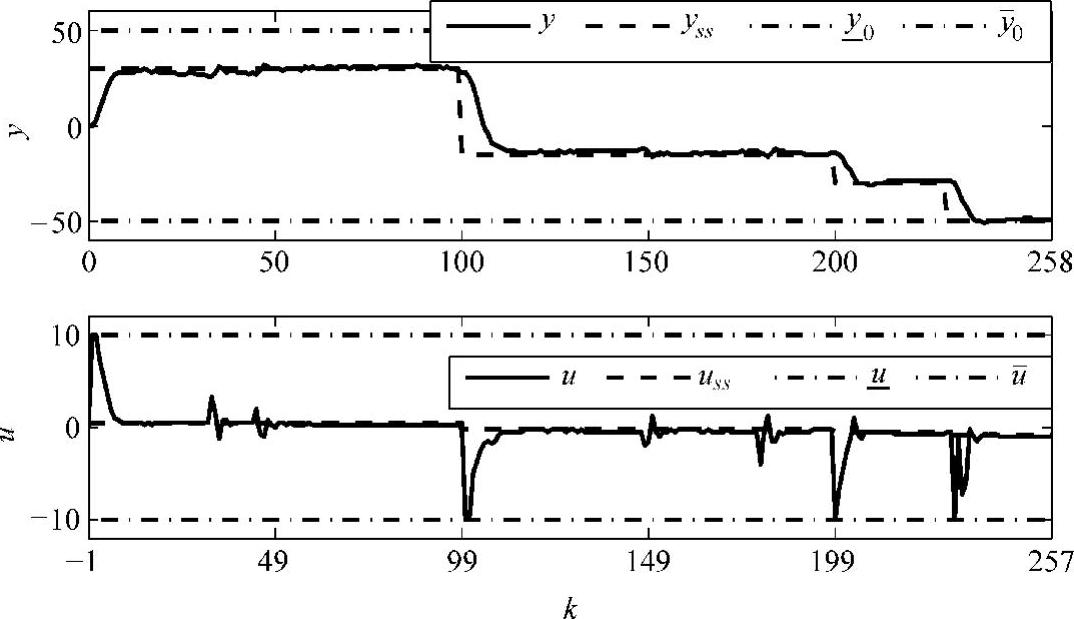
图8-16 三容水箱实验控制结果

注解8.1 实验中的电动调节阀（型号为QSVP-16K）执行精度较低（开度变化小于1%时即不执行），在系统基本达到稳态后，控制器计算的MV变化较小，电动调节阀不能有效执行，导致误差累积。实验中设置CV最大容许偏差限（即设定值和量测值间的差值范围，此限可以随时调整）来应对此问题。在系统基本达到稳态后，超出此限时，Λ减小到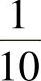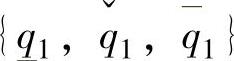，增大到10倍，故软件将计算出较大的MV变化量，驱动电动调节阀执行。图8-16中，时刻20～60之间和时刻140～195之间的四个MV的跃变即由参数改变导致。另外，由于稳态目标计算中没有用到CV的工程约束，故MV的幅值约束比动态控制模块中更紧，防止水的溢出。