PO-MOESP算法的应用及其特点

本小节内容原算法可参考参考文献[47，48，49]。MOESP（Multivariable Output-Error State sPace）是一种基于QR分解的方法，它有多种形式，以广泛采用的PO-MOESP（the ordinary MOESP scheme with instrumental variables constructed from Past input and Output measurements）为例介绍其算法实现。

执行如下的QR分解

由上式可得

U_f＝R₁₁Q^T₁，Y_f＝R₃₁Q^T₁+R₃₂Q^T₂+R₃₃Q^T₃（8-77）

将式（8-77）带入式（8-48）中，有

两边同乘以Q₂，利用正交矩阵的性质得到

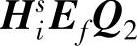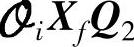根据参考文献[50]，。由于X_f有j列，式（8-79）右边第二项与第一项相比，是可以忽略的。由式（8-79）近似得到

上式表明的列空间与R₃₂的列空间相同；由于Q₂是正交矩阵，X_f的行空间与R₃₂的行空间相同。对式（8-80）进行SVD分解，可得(www.xing528.com)

利用能观性矩阵可确定

式（8-78）左乘Σ^T₂右乘Q₁，利用正交矩阵的性质得到

Σ₂^TR₃₁＝Σ^T₂H^d_iR₁₁+Σ^T₂H^s_iE_fQ₁ （8-82）

根据参考文献[50]，。式（8-82）右边第二项Σ^T₂H^s_iE_fQ₁与第一项Σ^T₂H^d_iR₁₁相比，是可以忽略的。由式（8-82）近似得到

Σ^T₂H^d_i＝Σ^T₂R₃₁R^-11₁ （8-83）

利用前面的式（8-73）所采用的方法可确定B、D。