本小节内容原算法可见参考文献[14]。回归分析法(RegressionAnalysisAp-proach,RAA)利用了预测器形式的状态空间模型进行推导,但本质上是采用新息形式状态空间模型的子空间辨识技术。由式(8-34),有
其中,BK=B-KD。由上式迭代可得
同理可得xi+1,…,xi+j-1,由这j个方程组成如下的矩阵方程:
Xf=ΦyYp+ΦuUp+ΦxXp (8-60)
其中,{Φu,Φy}与上节的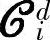 类似,即
类似,即
Φu=[Ai-1KBK … AKBKBK],Φy=[Ai-1KK … AKKK]
Φx=(A-KC)i。由于稳态Kalman滤波的稳定性,对于i→∞,Φx→0,则有
Xf=ΦyYp+ΦuUp (8-61)
记Zp=[YTpUTp]T,故
Xf=[ΦyΦu]Zp=LpZp (8-62)
将式(8-62)带入式(8-48)并重写为
Yf=LzZp+HdiUf+HsiEf (8-63)
其中,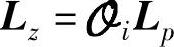 。对照式(8-10)和式(8-63),利用斜向投影相关结果得到
。对照式(8-10)和式(8-63),利用斜向投影相关结果得到
注意: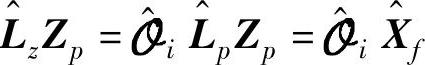 。
。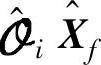 是对
是对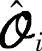 的列进行线性组合后的结果,也是对
的列进行线性组合后的结果,也是对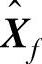 的行进行线性组合的结果。同时,
的行进行线性组合的结果。同时,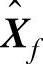 行满秩而
行满秩而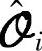 列满秩[前者因为j充分大、(A,[B,K])能控且输入u是f+p阶持续激励的;后者因为(C,A)是能观的]。故
列满秩[前者因为j充分大、(A,[B,K])能控且输入u是f+p阶持续激励的;后者因为(C,A)是能观的]。故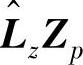 的列空间与
的列空间与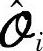 列空间相同,而其行空间与
列空间相同,而其行空间与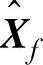 的行空间相同。因此很容易通过SVD分解得到
的行空间相同。因此很容易通过SVD分解得到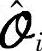 和
和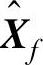 ,进而确定系统矩阵。(https://www.xing528.com)
,进而确定系统矩阵。(https://www.xing528.com)
线性回归分析法的算法步骤如下:
(1)根据式(8-64)计算得到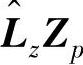 ;
;
(2)对 进行SVD分解,有
进行SVD分解,有
其中,Λ2的奇异值比Λ1的奇异值要小得多。根据奇异值大小确定信号子空间Σ1Λ1VT1和噪声子空间Σ2Λ2VT2。通过观察所有奇异值,选取nx个最大的值置于Λ1而相对较小的值置于Λ2中,nx便是系统阶次(状态维数)。值得指出,这种人工确定nx的方式淡化了关于噪声的假设的严格意义,因此得到的状态空间模型是近似的。
(3)取矩阵T=Λ1/21,得到
(4)计算系统矩阵
为了后面方便表达,将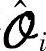 简写为
简写为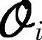 。矩阵C可从
。矩阵C可从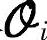 中提取得到
中提取得到
其中,标点“:”的使用同MATLAB。由矩阵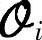 的移不变性可得
的移不变性可得
其中,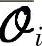 为移去前ny行的
为移去前ny行的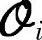 ,
, 为移去后ny行的
为移去后ny行的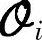 ,因此
,因此
在式(8-63)两边分别左乘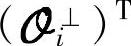 和右乘
和右乘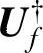 。由Ef和Uf不相关知
。由Ef和Uf不相关知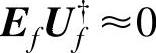 (见引理8.1)。另外,
(见引理8.1)。另外,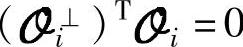 。故近似得到
。故近似得到
由式(8-66)可知,可取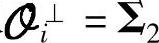 。式(8-71)可重写为
。式(8-71)可重写为
通过重组式(8-72)得到
由最小二乘法求解超定线性方程组可求得矩阵B和D。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




