基于新息形式状态空间描述基本思想：子空间辨识

对基于新息形式状态空间描述的开环子空间辨识，假设如下：

（1）输入信号u是f+p阶持续激励的；

（2）新息序列e_k是白噪声过程，与输入u_k和过去的输出不相关；

（3）系统是能控能观（最小实现）的，即（C，A）能观保证可辨识，（A，[B，K]）能控保证系统模态均可由外部输入和噪声充分激励；

（4）系统是渐近稳定的。

对Hankel矩阵容易得到如下有用的结论。

引理8.1 当j很大时，

（1）若e_k与u_k不相关，则E_i|2i-1U^T_i|2i-1≈0，也称为E_i|2i-1与U_i|2i-1不相关，同时E_i|2i-1U^†_i|2i-1≈0；

（2）若e_k与u_k不相关，则E_i|2i-1U^T_0|i-1≈0，也称为E_i|2i-1与U_0|i-1不相关，同时；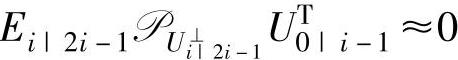

（3）若e_k与过去的y_k不相关，则E_i|2i-1Y^T_0|i-1≈0，也称为E_i|2i-1与Y0|i-1不相关，同时。

证明：结论中的定义部分根据第1章关于不相关的定义得到。由于U^†_i|2i-1＝U^T_i|2i-1（U_i|2i-1U^T_i|2i-1）^-1和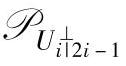＝I-U^T_i|2i-1（U_i|2i-1U^T_i|2i-1）^-1U_i|2i-1，容易得到结论的其他部分。

证毕

在子空间辨识方法中，通常是在未知状态空间模型的情况下，通过过程的输入输出数据确定动态系统的状态序列，基此使用回归方法得到系统矩阵。经典的辨识算法通过输入输出数据得到系统的输入输出模型，基此可得到各种状态空间实现，而Kalman滤波可实现对状态的估计。采用子空间辨识算法，可在未得到状态空间模型前，就估计出Kalman状态序列，这是其区别于其他输入输出模型辨识方法的主要不同之处。

子空间辨识法确定系统矩阵，主要有两种思路：

（1）利用子空间矩阵求解(www.xing528.com)

本章后面三节采用的都是这种思路。根据前面的推导可知，子空间矩阵方程中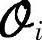是关于A和C的子空间矩阵，H^d_i是关于B和D的子空间矩阵，故若能得到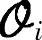和H^d_i的估计值，则可求得系统矩阵。

（2）利用Kalman状态序列直接求解

由式（8-47）得到如下两个状态矩阵：

由式（8-48）得到

Y_i|i＝CX_i+DU_i|i+E_i|i （8-53）

将式（8-51）代入式（8-52）的结果与式（8-53）联立，可得到

基于同样的初始状态矩阵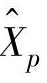，估计两个状态矩阵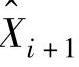和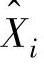，分别替代式（8-54）中的X_i+₁和X_i。当采用Kalman滤波时，由新息组成的E_i|i与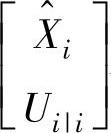不相关，故可采用最小二乘法确定系统矩阵

一般地，满足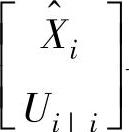与E_i|i不相关是理论上常用的假设（见8.1.1节）。

根据需要，可以按如下方法得到噪声协方差阵和Kalman预报器增益。噪声估计值可由最小二乘问题的残差得到

噪声的协方差阵为

求解如下代数Riccati方程（见第2章）：

P＝APA^T-（APC^T+R_e12）（CPC^T+R_e2）^-1（APC^T+R_e12）^T+R_e1

得到解P^*≥0，从而可计算稳态Kalman预报器增益

K＝（AP^*C^T+R_e12）（CP^*C^T+R_e2）^-1 （8-57）