子空间辨识研究时常用的状态空间方程有三种表达形式:过程形式、新息形式和预测器形式,这三种形式可以相互转换。
1.过程形式
对线性时不变离散时间系统,其过程形式的状态空间方程为
其中, 、
、 和
和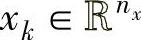 分别为过程的输入、输出和系统状态,{A,B,C,D}为系统参数矩阵,
分别为过程的输入、输出和系统状态,{A,B,C,D}为系统参数矩阵,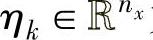 为输入噪声,
为输入噪声,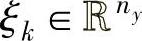 为观测噪声且满足
为观测噪声且满足
κpq为Kronecker符号。这表明ηk和ξk都是白噪声。
由第2章知,如果假设S=0,对线性系统的状态空间描述并没有带来更多的特殊性。但是,假设S≠0在子空间辨识中更加方便,其对应的Kalman滤波方法见第2章。
对实际应用,辨识以上状态空间模型时{x,u,y}应该是{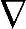 x,
x,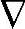 u,
u,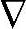 y}或者{Δx,Δu,Δy}的省略形式。采用{
y}或者{Δx,Δu,Δy}的省略形式。采用{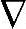 x,
x,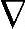 u,
u, y}时,需要知道系统的稳态工作点{u,y}eq;采用{Δx,Δu,Δy}时,不需要知道系统的稳态工作点。
y}时,需要知道系统的稳态工作点{u,y}eq;采用{Δx,Δu,Δy}时,不需要知道系统的稳态工作点。
2.新息形式
对线性时不变离散时间系统,其新息形式的状态空间方程为
其中,ek为与输入uk和过去的输出均不相关的白噪声序列。
通过Kalman预报器和符号置换,可发现式(8-30)和式(8-32)是一致的。如果式(8-30)是可检测的,则基于稳态Kalman预报器可估计系统状态,即
其中,K为Kalman预报器增益。定义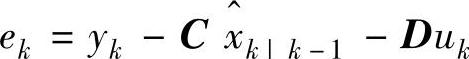 为新息,并简记
为新息,并简记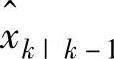 为xk,则可以得到式(8-32)。
为xk,则可以得到式(8-32)。
3.预测器形式(https://www.xing528.com)
以上新息形式的状态空间方程亦可转换为预测器形式:
其中,zk=[uTkyTk]T,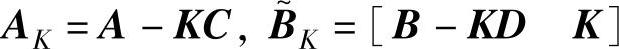 。如果式(8-30)是可检测的,总可以找到一个K,使得AK=A-KC稳定,所以对于不稳定系统进行闭环辨识时,预测器形式更为有利。
。如果式(8-30)是可检测的,总可以找到一个K,使得AK=A-KC稳定,所以对于不稳定系统进行闭环辨识时,预测器形式更为有利。
以新息形式状态空间描述为例,子空间辨识问题为:对于给定的L+1组输入输出采样数据{uk,yk}Lk=0,确定系统阶数nx和系统矩阵(A,B,C,D,K)。针对新息形式的状态空间描述,常用矩阵的定义如下:
•数据d的Hankel矩阵,d∈{u,y,e},D∈{U,Y,E}:
其中下标t1|t2表示Hankel矩阵的第一列起始于t1时刻结束于t2时刻;
•状态序列矩阵: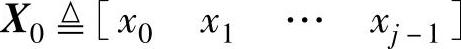 ,
,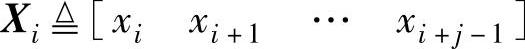 ;
;
•扩展能观性矩阵: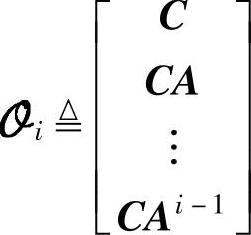 ;
;
•确定输入项的逆向扩展能控性矩阵: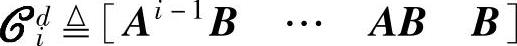 ;
;
•随机输入项的逆向扩展能控性矩阵: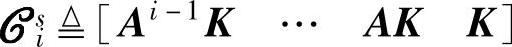 ;
;
•确定输入项的下三角分块Toeplitz矩阵:
•随机输入项的下三角分块Toeplitz矩阵:
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




