【摘要】:下面从线性回归问题的最小二乘解的角度介绍正交投影和斜向投影。正交投影具有如下性质:图8-1 二维Euclid空间正交投影2.斜向投影对于有两个输入量f和u的情况,是式(8-2)的推广,即其中,L和H为参数矩阵。区别于正交投影算子W,称F/U为斜向投影算子。
下面从线性回归问题的最小二乘解的角度介绍正交投影和斜向投影。
1.正交投影
给定输入向量w(k)、输出向量y(k)和噪声向量ξ(k),定义线性关系

其中, 为参数矩阵。对于w(k)、y(k)的L+1个观测值,有
为参数矩阵。对于w(k)、y(k)的L+1个观测值,有
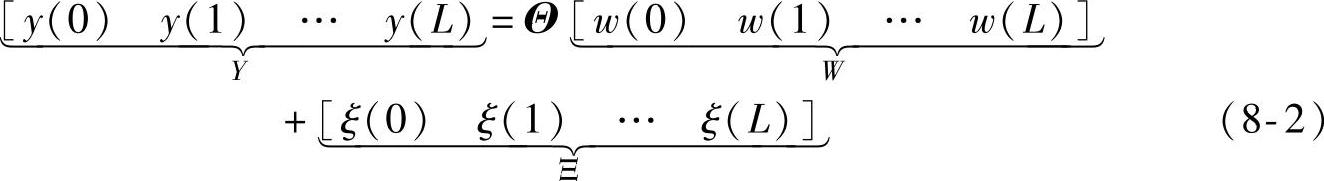
记 的最小二乘估计量为
的最小二乘估计量为 。定义二次准则函数为
。定义二次准则函数为

令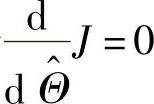 ,当WWT可逆时,得到
,当WWT可逆时,得到

这是众多线性参数回归的方法之一。如果ξ(k)的均值为零,且ξ(k)和w(k)不相关,则该估计值具有无偏性。如果式(8-1)表示系统方程,则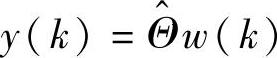 表示该系统模型。则基于模型的最小二乘预测值为
表示该系统模型。则基于模型的最小二乘预测值为
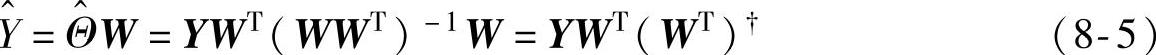
定义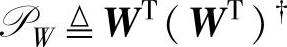 为在矩阵W的行空间上的投影算子,则Y的最小二乘预测值可以视为Y的行空间在W的行空间上的正交投影,记作Y/W。故
为在矩阵W的行空间上的投影算子,则Y的最小二乘预测值可以视为Y的行空间在W的行空间上的正交投影,记作Y/W。故

引入残差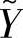 ,即
,即

则有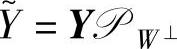 ,
,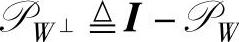 。故
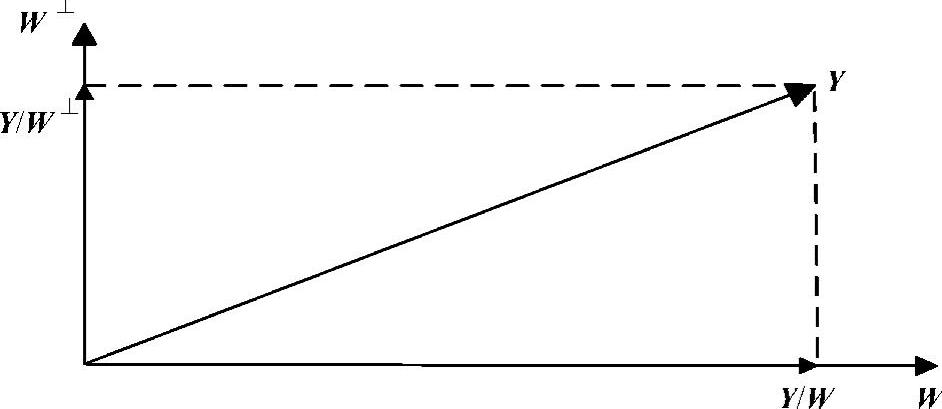
。故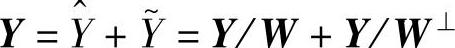 。可通过图8-1在二维平面空间解释正交分解:向量Y可分解为W上的投影Y/W和W⊥上的投影Y/W⊥。正交投影具有如下性质:
。可通过图8-1在二维平面空间解释正交分解:向量Y可分解为W上的投影Y/W和W⊥上的投影Y/W⊥。正交投影具有如下性质:
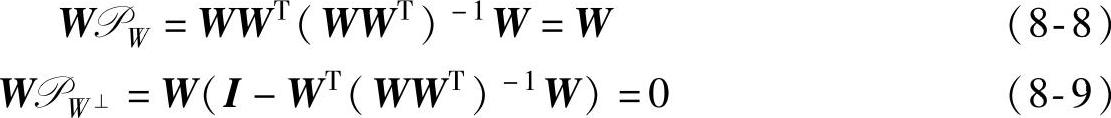
 (https://www.xing528.com)
(https://www.xing528.com)
图8-1 二维Euclid空间正交投影
2.斜向投影
对于有两个输入量f(k)和u(k)的情况,是式(8-2)的推广,即
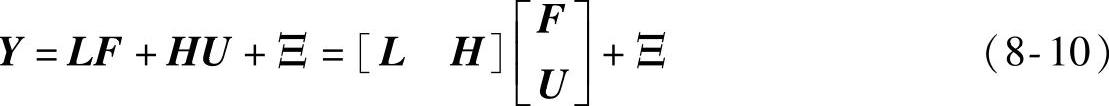
其中,L和H为参数矩阵。当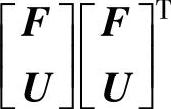 可逆时,基于最小二乘法可以得到L和H的估计值
可逆时,基于最小二乘法可以得到L和H的估计值
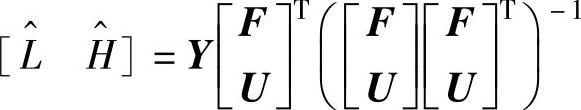
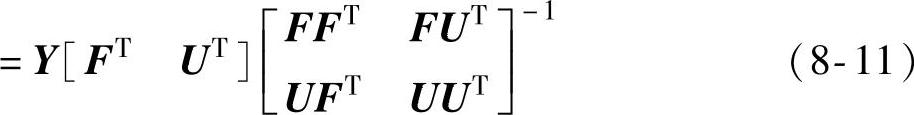
由分块矩阵求逆公式,采用式(8-11)可得
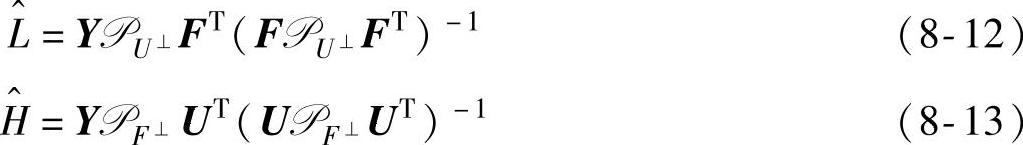
如果ξ(k)的均值为零,且ξ(k)和{f,u}(k)不相关,则以上估计值具有无偏性。则基于模型的最小二乘预测值为
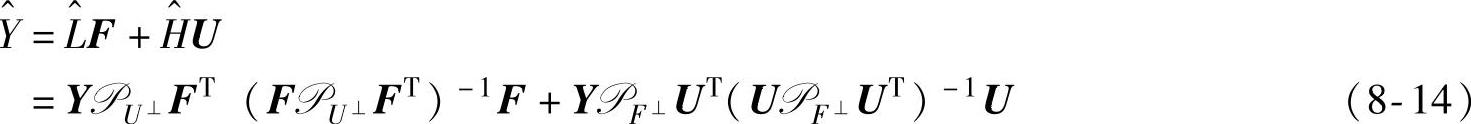
定义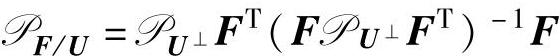 表示沿着U的行空间在F的行空间上的投影算子。区别于正交投影算子W,称F/U为斜向投影算子。则Y的最小二乘预测值可以斜向分解为
表示沿着U的行空间在F的行空间上的投影算子。区别于正交投影算子W,称F/U为斜向投影算子。则Y的最小二乘预测值可以斜向分解为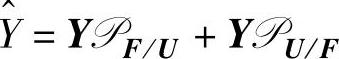 ,记为
,记为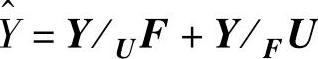 。结合前面的正交分解和斜向分解,得到
。结合前面的正交分解和斜向分解,得到
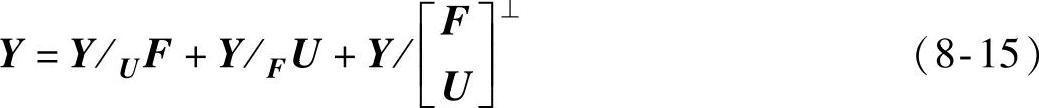
如图8-2所示。斜向投影具有如下性质:
F/FU=0 (8-16)
F/UF=F (8-17)
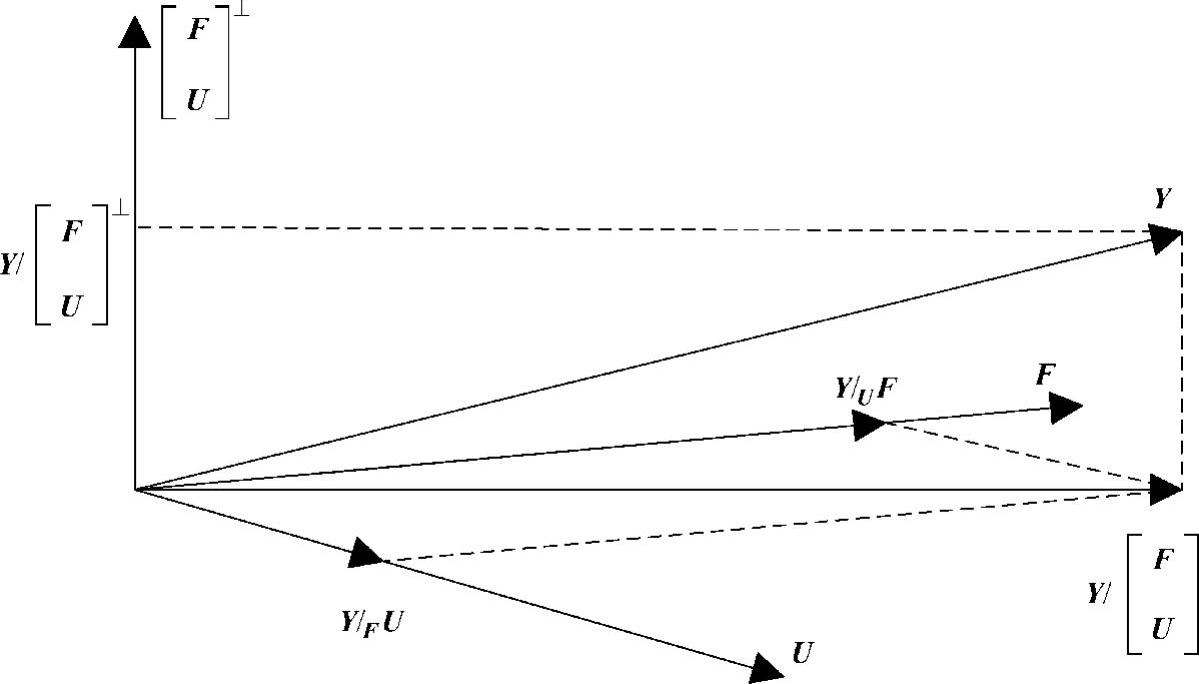
图8-2 三维空间斜向投影
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




