模型辨识方法：探索7.3.3的实践应用

多变量数学模型体现了多个输入变量（独立变量）与多个输出变量（依赖变量）之间的交互影响关系，但是在模型辨识过程中要注意与工艺条件的配合。大型生产过程通常具有上下游特点，由工艺顺序可知，下游的输入变量不会对上游输出造成影响，但如果不加分析地将上下游输入输出数据统一放在一起辨识，将得到下游输入对上游输出有影响的错误结论。即使不是源于这种上下游特点，也不是任意一个独立变量的改变都影响任意一个依赖变量。如果所有独立变量和所有依赖变量之间都有动态对应关系，原则上是可以同时辨识多入多出模型的；但考虑到有些独立变量和依赖变量之间没有动态关系是常见的事实，故辨识方法中采用的是案件分组的形式。

1.辨识案件分组

如果一部分依赖变量y^（j）与一部分独立变量w^（j）之间存在完全的动态对应关系（或不确定其中某些独立变量和依赖变量之间是否存在动态对应关系），则可以将y^（j）与w^（j）之间动态模型的辨识作为一个案件组，称为案件组j。这里关于案件组的思想来源于对Aspen Technology的工业MPC软件的学习，特此说明。

同一案件组j中可能同时包括积分型和稳定型依赖变量。根据划分的案件组进行辨识后，如果进一步确定了某些独立变量和依赖变量之间不存在动态对应关系，则需要重新划分部分案件组并重新辨识。案件组的划分在最终确定之前可能要调整多次。

2.针对稳定型依赖变量的案件数据准备

设y^s_j属于案件组，则在辨识y^s_j与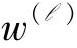之间的动态关系模型时，首先构造矩阵。每一行的形式为

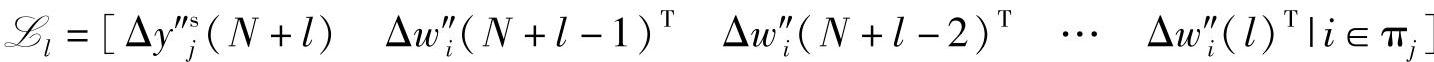
其中，l∈{1，2，…，L-N}，下角标i在中的出现和排列是按照逐渐递增的方式。如果的计算涉及到坏数据，则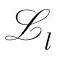不置入中，否则在下面增加一行。随着l∈{1，2，…，L-N}每增加1，或者在下面增加1行，或者不变。最后得到的形如下式：

其中，Y_j和Φ_j分别为Δy^s_j和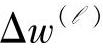的数据形成的矩阵。

将式（7-35）中对应于第j个依赖变量的部分重写为

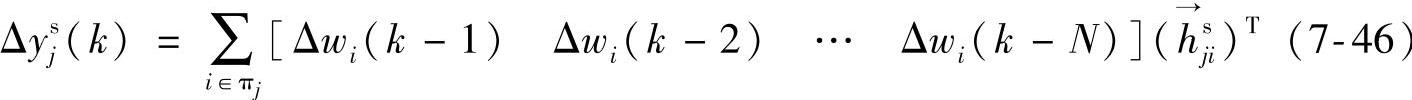
则当模型完全准确、数据全好、没有噪声时，应该满足

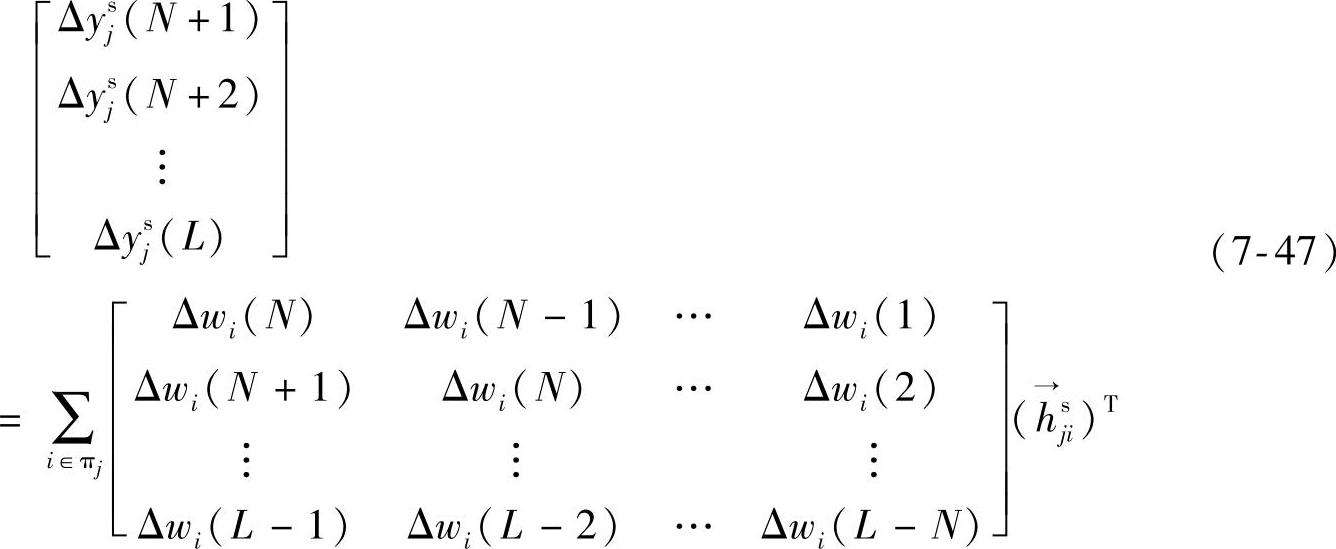
可将式（7-47）简写成如下形式：

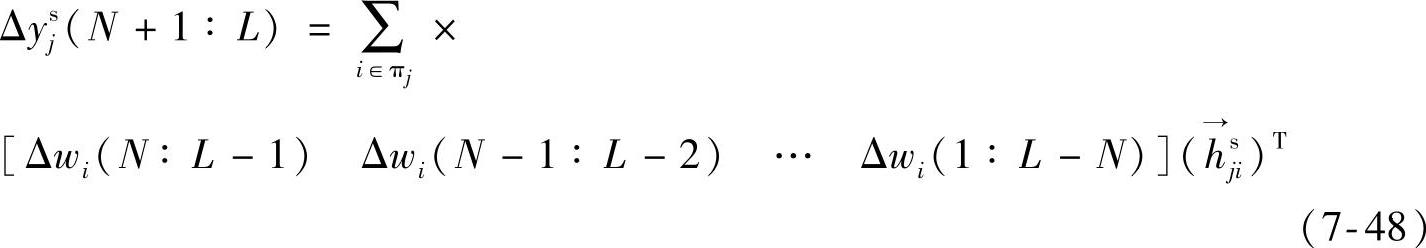
由于做了坏数据的剔除、插值和数据平滑处理，不是用式（7-47）～式（7-48），而是用下式做模型参数回归：

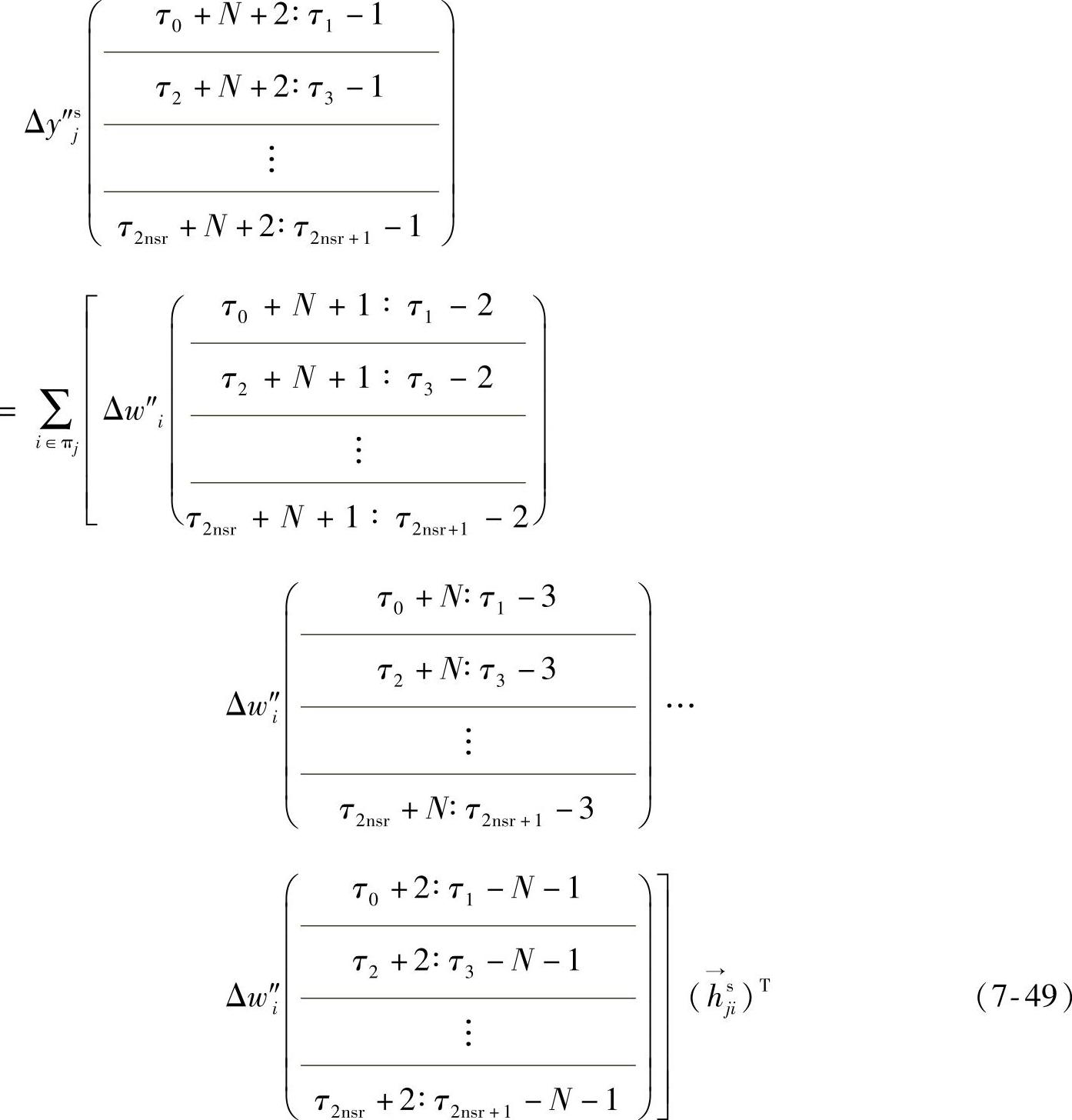
其中，τ_i（i∈{0，1，…，2nsr+1}）为整数，nsr为“number of sections removed”的缩写。注意此处τ不同于式（7-39）中的t。

例7.1 假设τ₀＝-1、τ₁＝L₁+2、τ₂＝L₂、τ₃＝L+1，则式（7-49）成为

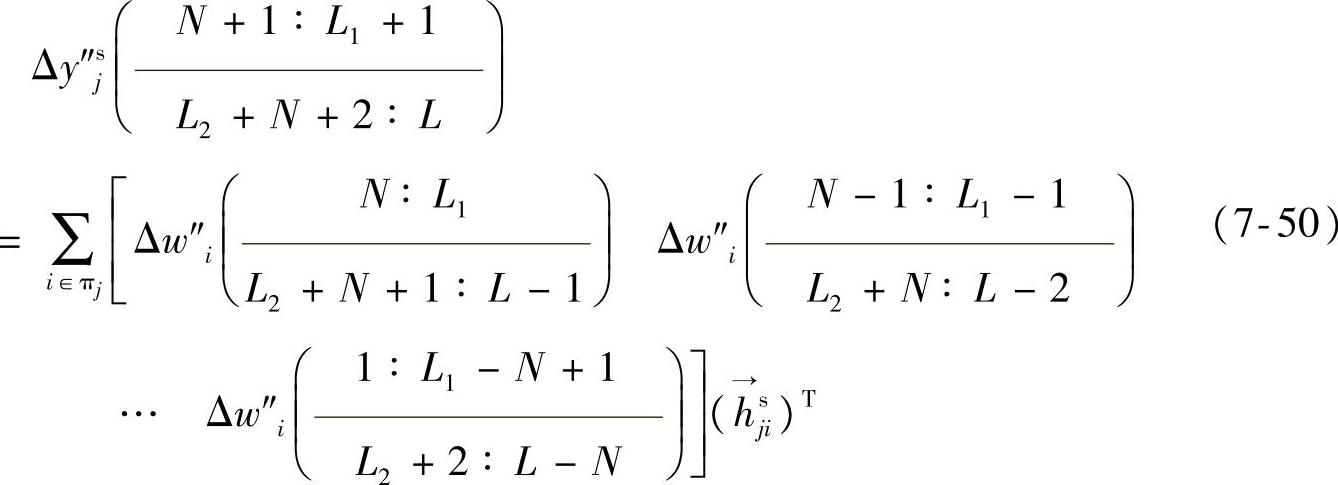
并等价于

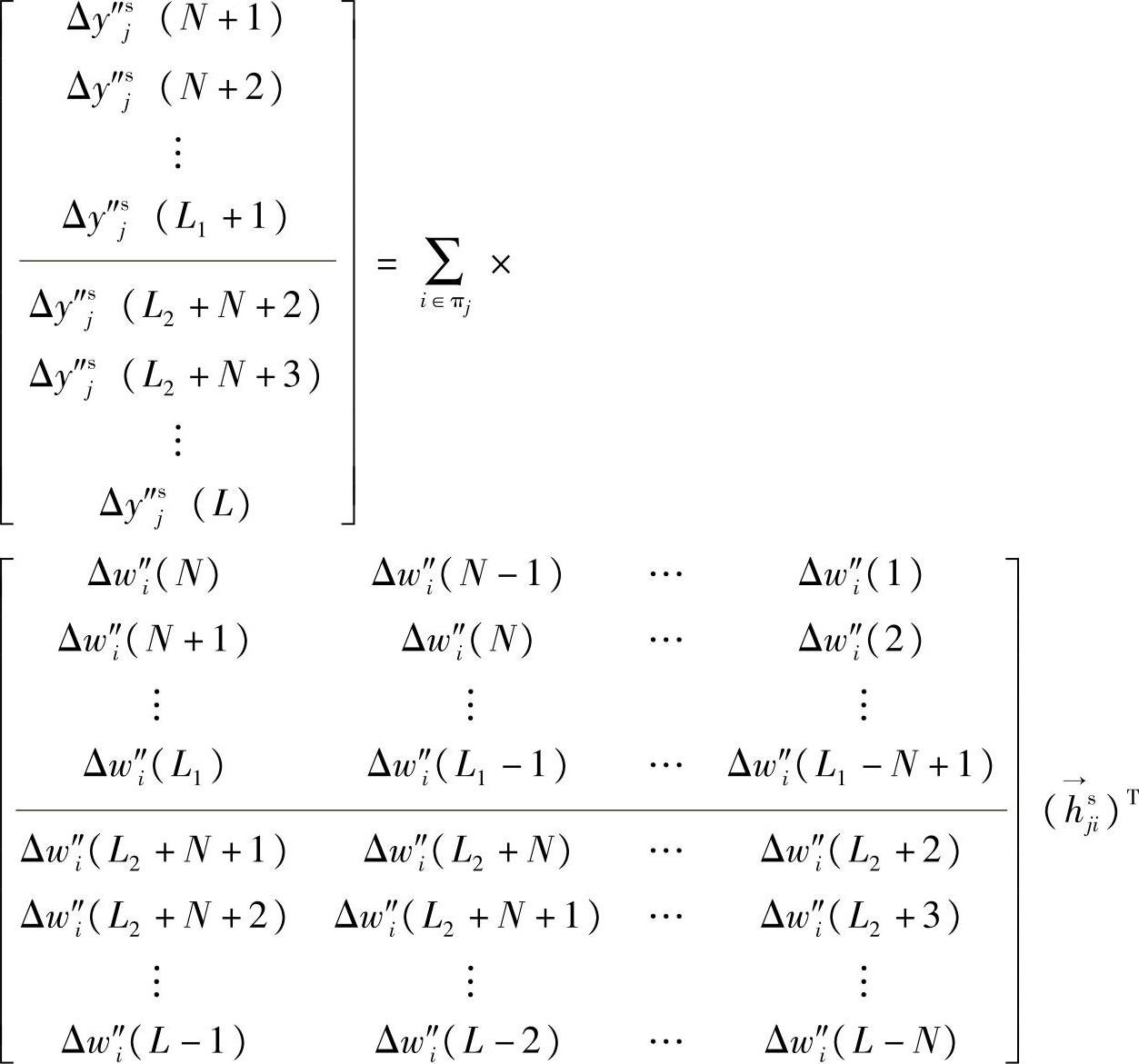
3.针对积分型依赖变量的数据准备

设y^r_j属于案件组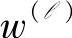之间的动态关系模型时，首先构造矩阵。每一行的形式为

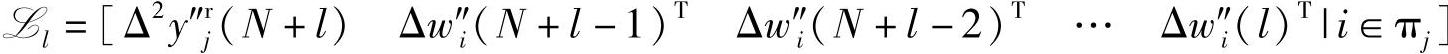
其中，l∈{1，2，…，L-N}，下角标i在中的出现和排列是按照逐渐递增的方式。如果的计算涉及到坏数据，则不置入中，否则在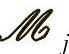下面增加一行。随着l∈{1，2，…，L-N}每增加1，或者在下面增加1行，或者不变。最后得到的形如下式：

其中，Y_j和Φ_j分别为Δ²y^r_j和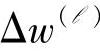的数据形成的矩阵。

将式（7-36）中对应于第j个依赖变量的部分重写为

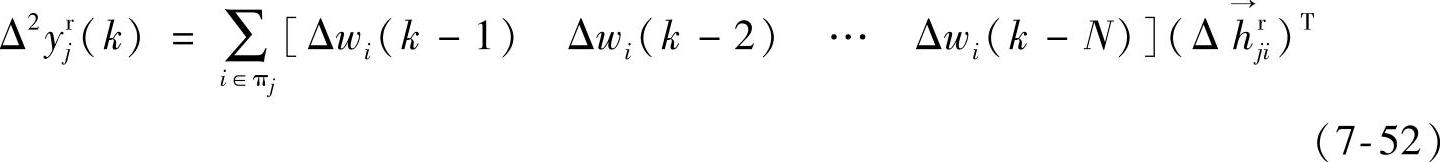
则当模型完全准确，数据全好，没有噪声时，应该满足

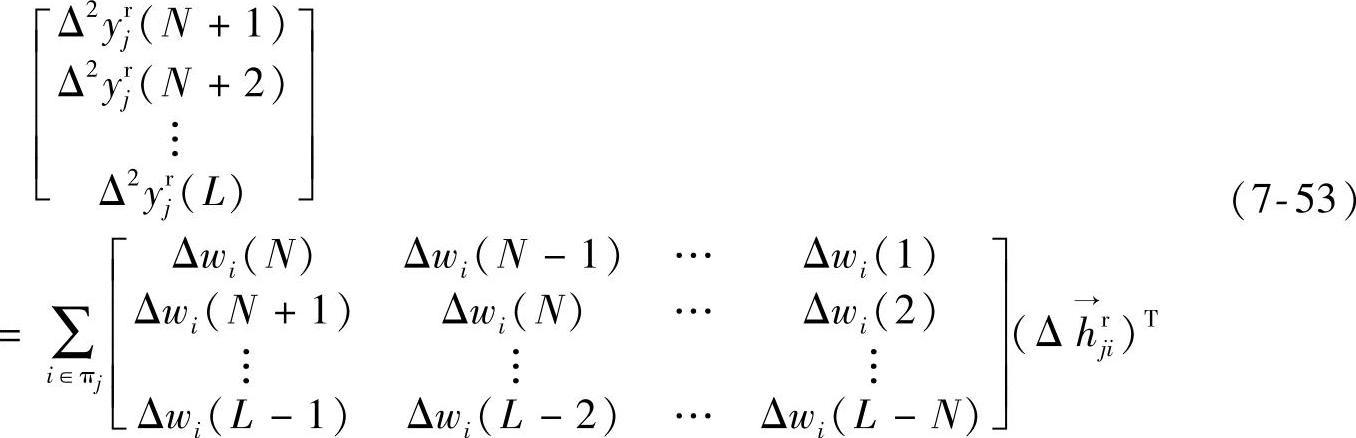
可将式（7-53）简写成如下形式：

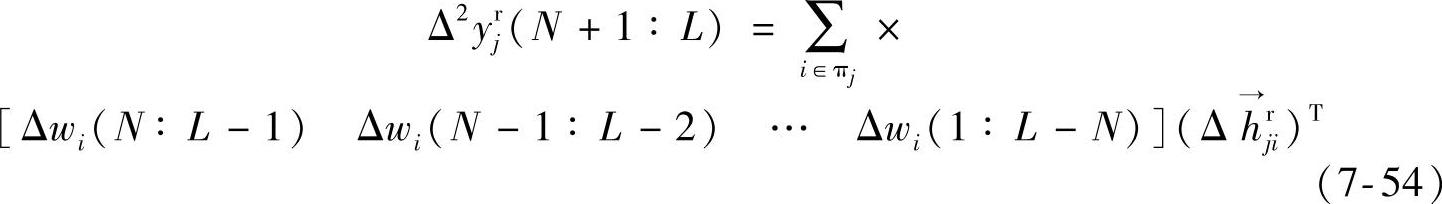
由于做了坏数据的剔除、插值和数据平滑处理，不是用式（7-53）～式（7-54），而是用下式做模型参数回归：

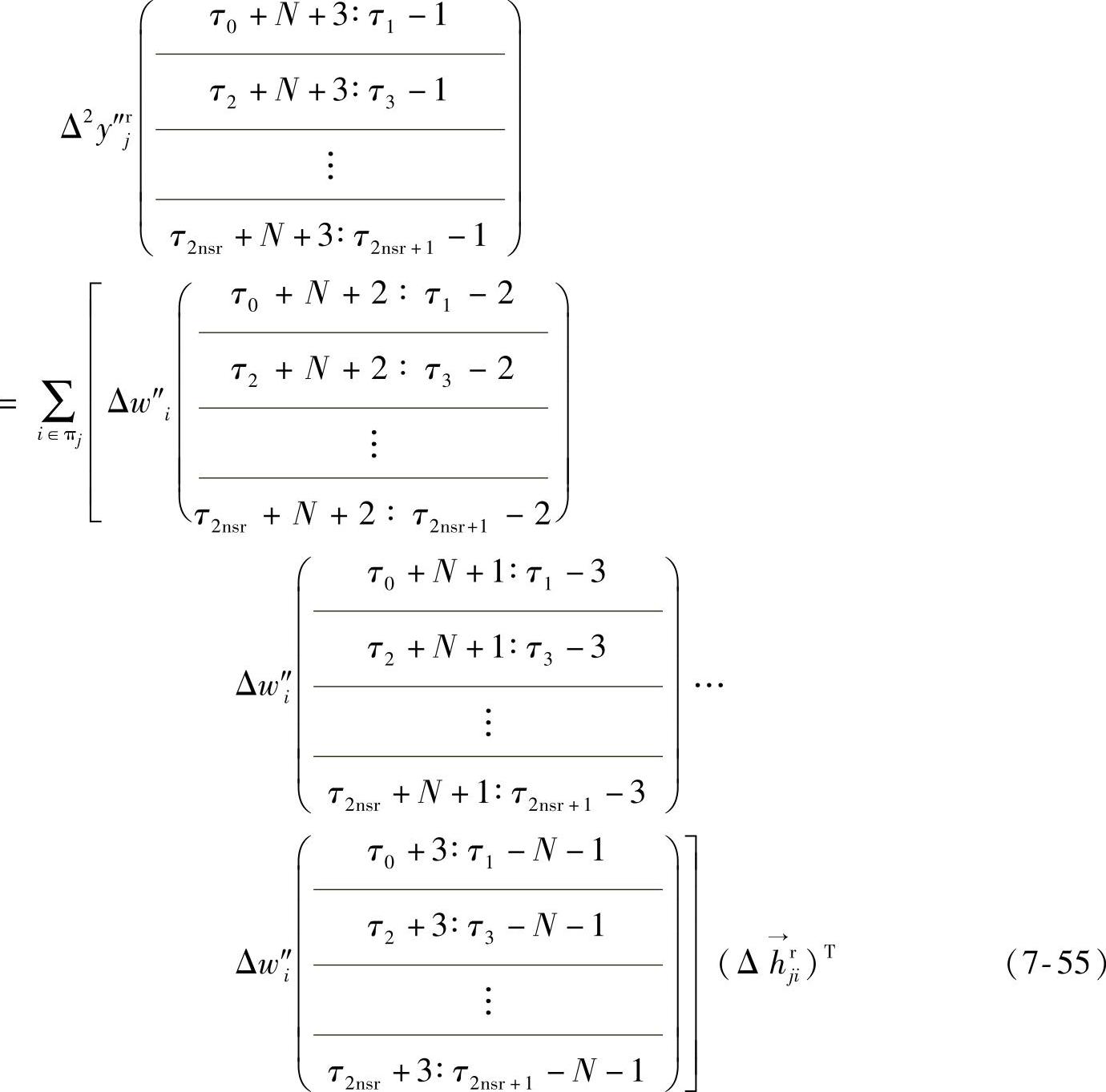
注意此处τ不同于式（7-39）中的t。式（7-55）中的每个数据段长度比式（7-49）少一个的表达方式，仅仅表示积分型CV的二阶差分可能造成数据长度多减小1——但这不是肯定的（如：坏的数据是w_i的情况）。

4.参数回归的最小二乘解

将式（7-49）或者式（7-55）简记为

Y_j＝Φ_jθ_j （7-56）

其中，θ_j由待辨识参数组成，即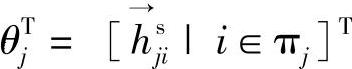或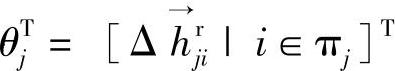。在θj中，i的出现和排列是按照逐渐递增的方式，即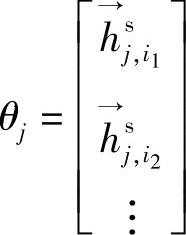或者，i₁＜i2＜…且i₁，i₂，…∈π_j。

实际上，由于数据中含有噪声（对数据平滑也不能完全消除噪声影响），模型有截断误差和不可避免的系统非线性、时变特性等，式（7-56）是不能严格满足的。引入残差，将式（7-56）改写为

其中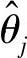，表示θ_j的估计值；ε_j为残差序列组成的向量。

一般来说，参数估计的准则是最小化

其中，μ≥0为平滑因子，Π≥0有多种选择方法。当希望惩罚待辨识参数的变化速率，并且希望越接近稳态参数变化越小时，可以取（见参考文献[5]）

Π＝Γ^TΛΓ，Γ＝diag{Γ_i|i∈π_j}，Λ＝diag{Λ_i|i∈π_j}

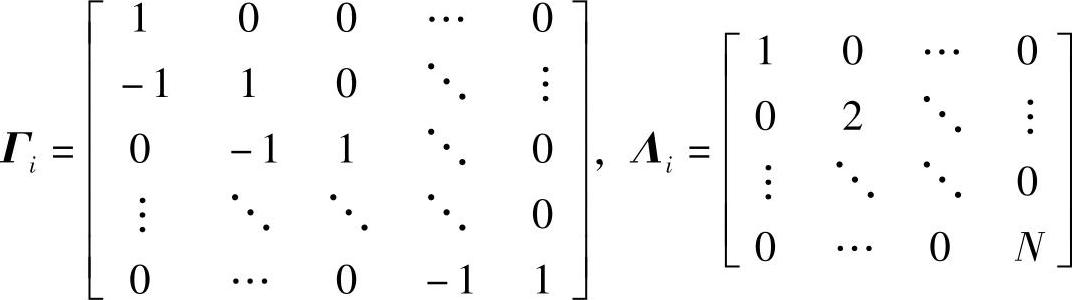
最小化J相当于求如下关于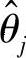的线性方程组的最小二乘解：

该最小二乘解为(www.xing528.com)

如果y′_j和y_j在同一个案件组，则

以上式（7-60）、式（7-61）采用了同一个（Φ^T_jΦ_j+μΠ）^-1Φ^T_j，从而简化计算过程，这是采用辨识案件分组的优势。对同一组，可以一次算出所有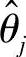，但这样做对计算量没有任何降低，故这里的脉冲响应模型辨识本质上不是基于多入多出机理的。

注解7.3 对应式（7-58），标准的QP目标函数为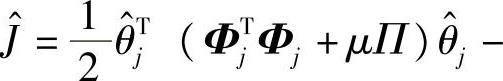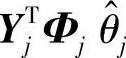。在如下两种情况下，某些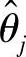的元素是可以事先确定的：

•某些输入输出之间的时滞已知，相应的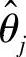的某些元素为0；

•某些MV为PID的设定值，采用PID可达到无静差控制，这样造成有些SISO模型的稳态增益为0（阶跃响应的第N个系数为0），有些SISO模型的稳态增益为1（阶跃响应的第N个系数为1）。因此，可以已知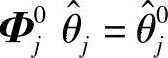，其中，Φ⁰_j为行满秩矩阵。这样辨识的优化问题为

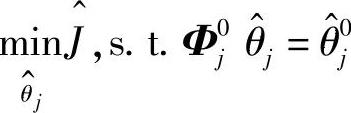
根据第3章关于等式约束QP问题的解法，得到

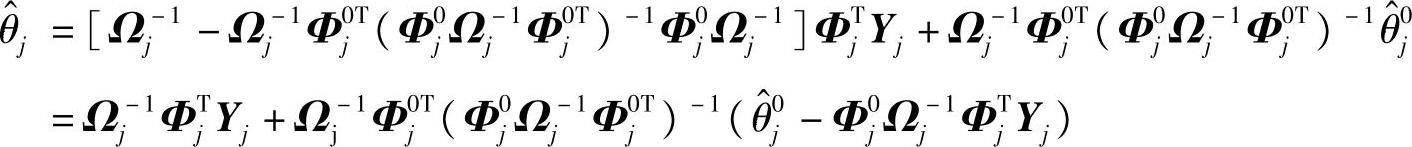
其中，Ω_j＝Φ^T_jΦ_j+μΠ。

5.用SVD分解得到参数估计的最小二乘解

一般来说，对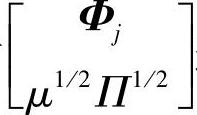进行SVD分解，将得到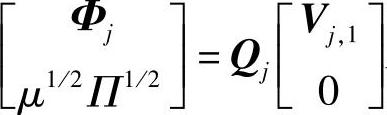R_j，其中，V_j，1为对角非奇异方阵。在式（7-59）两边都左乘Q^-1_j＝Q^T_j，得到

其中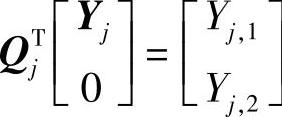，，不表示Y_j与Y_j，1有同样维数。在最小化式（7-58）的意义下，得到最小二乘解为

由于V_j，1为对角非奇异方阵，其逆是可以非常容易地求解的。

注解7.4 如果取μ＝0，而且数据质量不好，则对Φ_j进行SVD分解，可能得到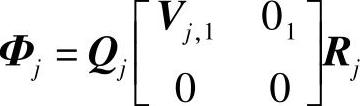，其中，V_j，1为对角非奇异方阵，0₁为零矩阵，这时最小二乘解为

如果在式（7-64）中01的维数不为零，则软件应该给出“数据不合格”的信息指示。

6.脉冲响应系数的滤波

对积分型依赖变量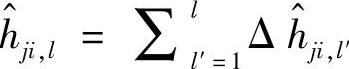，。对所有依赖变量，在得到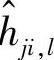的值后，要对其做滤波处理。以一阶惯性滤波为例，得到在控制中采用的阶跃响应系数如下：

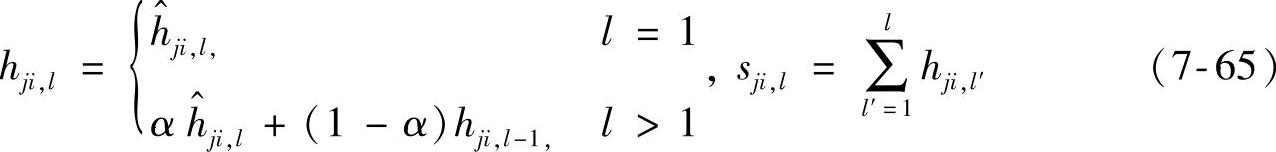
在现有的模型辨识软件中，积分过程需要人工指定，而且在模型输出文件中，通常由标志位标识某组模型参数为积分依赖变量的模型。

例7.2 考虑SISO系统的FIR模型

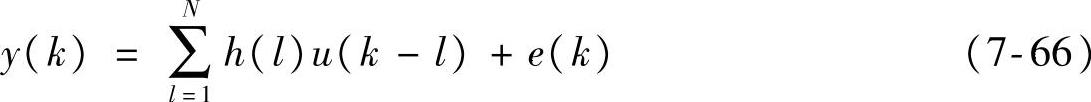
其中，e（k）代表建模误差。展开式（7-66），则有

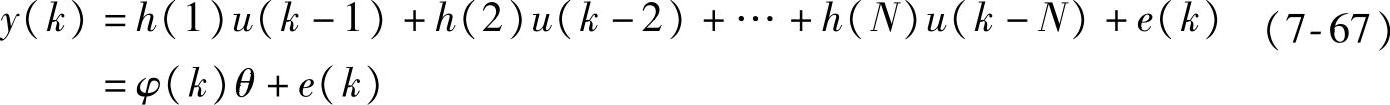
其中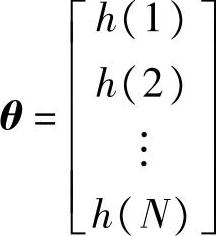，，φ（k）＝[u（k-1），u（k-2），…，u（k-N）]。

假设测试实验阶段采集的独立变量、依赖变量序列为{u（1），u（2），…，u（L）}、{y（1），y（2），…，y（L）}。将独立变量、依赖变量数据带入式（7-67），写成矩阵形式

y＝Φθ+e （7-68）

其中，

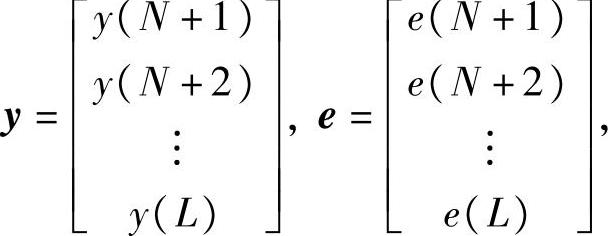
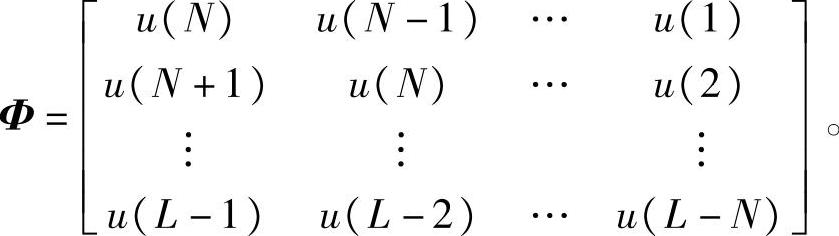
将残差的范数最小化，即

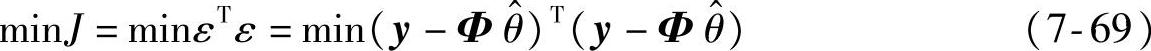
可得，

其中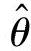，是θ的估值。

例7.3 （见参考文献[95]）采用例7.2的方法进行辨识，以说明采用最小二乘法辨识FIR模型参数的效果。在MATLAB语言SIMULINK平台下建立了实验环境，如图7-8所示，直接以随机数作为独立变量，并在依赖变量端施加了随机噪声。其中，两个随机数发生器的均值都为0，方差都为0.1，仿真平台的采样周期为1。独立变量、依赖变量数据如图7-9所示。

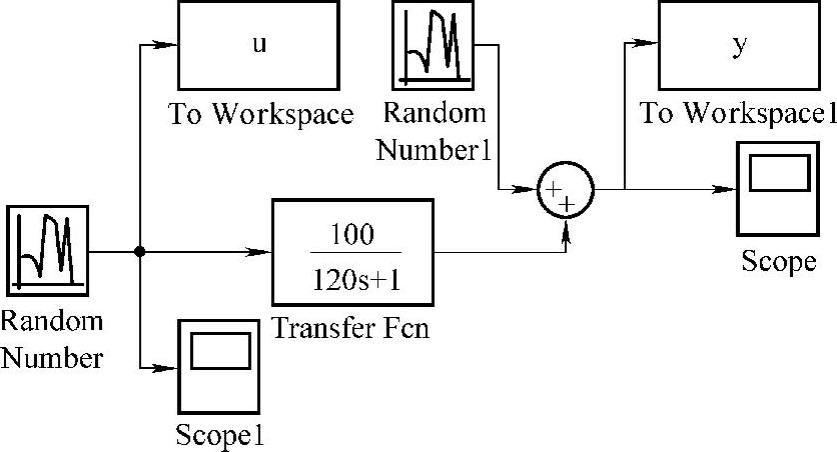
图7-8 MATLAB语言SIMULINK下实验系统

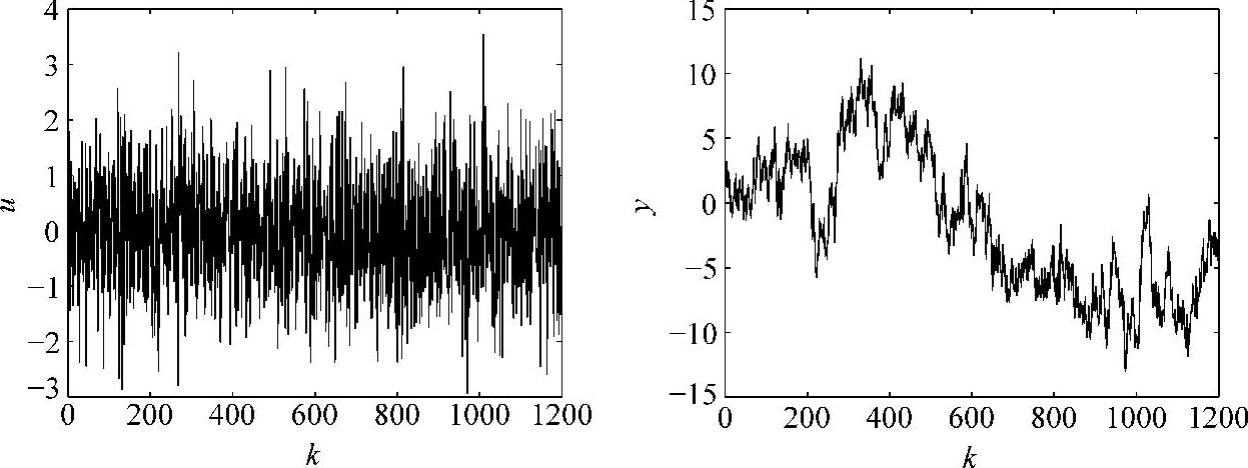
图7-9 独立变量（左）、依赖变量（右）采样数据

为了说明FIR模型辨识方法中数据长度与模型参数个数之间的简单关系，选取以下三组情况进行测试，它们的{数据长度，模型参数个数}分别为{1200，480}、{1200，600}、{1800，600}，相应的辨识结果（FIR和FSR）如图7-10、图7-11、图7-12所示，其中FIR图中同时包含了真实的脉冲响应参数。对这些辨识结果进行分析，可以得到以下的简单结论：首先，模型时域是FIR模型辨识的重要参数，对其选择不当将出现较大的误差；其次，待辨识参数较多的情况下，相应的独立变量、依赖变量数据长度也要足够大，否则会出现较大的误差（由于坐标范围较大，图7-10～图7-12中的阶跃响应显得较为平稳）。需要指出，在这个实验中待辨识的模型参数个数较多仅是为了说明辨识方法是否有效，在MPC工程应用中，采样周期一般以分钟为单位，模型时域要根据各子过程中稳态响应时间最长的一个来选定，一般取45～120个采样周期。

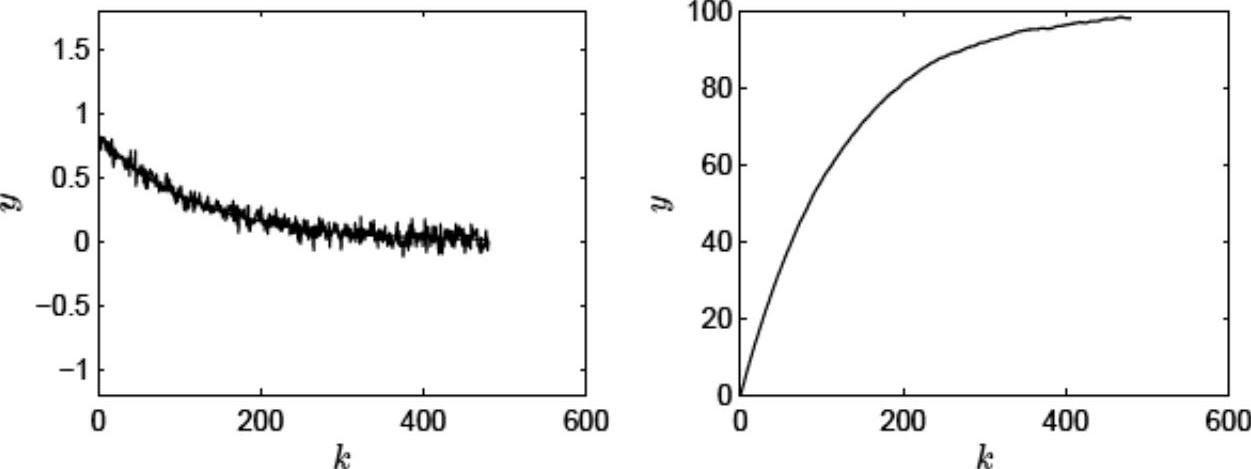
图7-10 数据长度为1200个、待辨识参数为480个情况下的模型输出结果

图7-11 数据长度为1200个、待辨识参数为600个情况下的模型输出结果

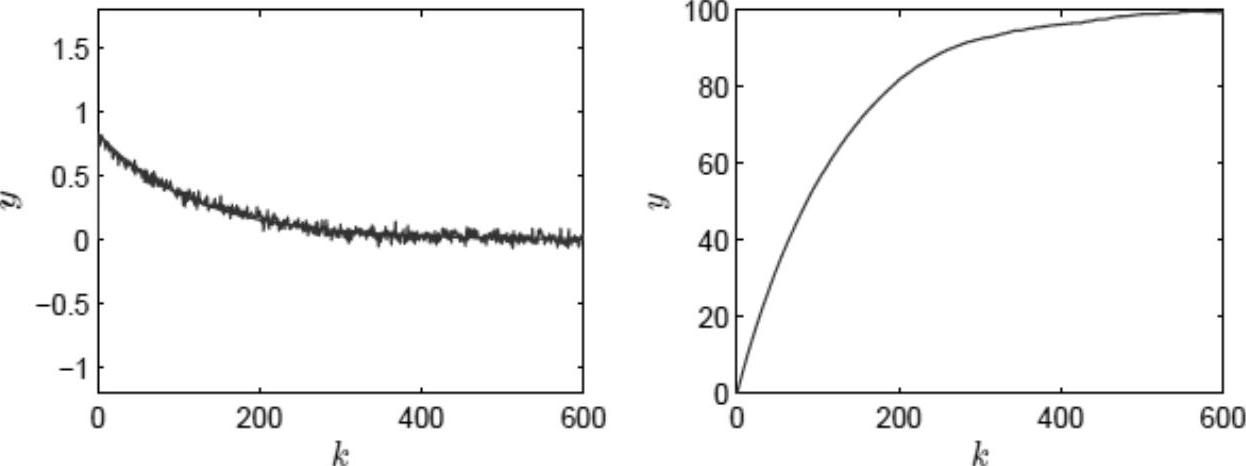
图7-12 数据长度为1800个、待辨识参数为600个情况下的模型输出结果