待辨识模型的详细描述

依赖变量y分为两类：稳定和一阶积分型，即，其中，上角标s和r分别表示稳定（stable）和积分（ramp）。不失一般性，假设，，n^s_y+n^r_y＝n_y。假设系统的稳态工作点为

辨识的目的是得到在稳态工作点附近的系统的近似线性模型。辨识中对稳定型依赖变量和积分型依赖变量明确地区别对待。

对稳定型依赖变量，采用如下的有限脉冲响应模型：

其中，H^s_l为脉冲响应系数矩阵；y^s（k）＝y^s（k）-y^s_eq；w（k-l）＝w（k-l）-w_eq。采用式（7-31）表示线性开环稳定模型的前提是H^s_l≈0，∀l＞N，而N为模型时域，故式（7-31）是对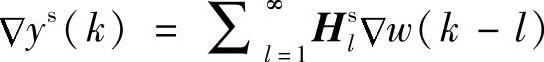的有效近似。

对一阶积分型依赖变量，采用如下的增量形式的有限脉冲响应模型：

其中，ΔH^r_l＝H^r_l-H^r_l-1，（Δy^r（k））＝Δ（y^r（k））＝Δy^r（k），而Δy^r（k）＝y^r（k）-y^r（k-1），y^r（k）＝y^r（k）-y^r_eq。采用式（7-32）表示线性开环一阶积分对象的前提是ΔH^r_l≈0，∀l＞N，即式（7-32）是对的有效近似。

由于采用式（7-31）～式（7-32）时，需要知道y^s_eq和w_eq，这在多数情况下是不容易做到的。若采用数据的增量值，则无需知道y^s_eq和w_eq。在式（7-31）～式（7-32）的两边都乘以Δ。注意Δ（y^s（k））＝Δy^s（k），Δ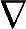（w（k-l））＝Δw（k-l）和Δ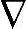（（Δy（k）））＝Δ²y（k）。得到

其中，Δ²y^r（k）＝y^r（k）-2y^r（k-1）+y^r（k-2）。合并式（7-33）～式（7-34）得到(www.xing528.com)

本节的最小二乘法，就是利用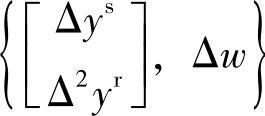的数据集，回归系数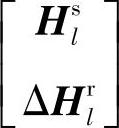，l∈{1，2，…，N}。

并非所有的独立变量和所有的依赖变量之间都有动态因果关系。记H_l为

如果存在i∈{1，2，…，n_w}和j∈{1，2，…，n_y}，使得对∀l∈{1，2，…，N}，成立h_ji，l＝0，则这些h_ji，l不宜出现在被辨识的参数中。如果这些已知为0的参数被辨识，辨识结果一般来说不是0，因此会影响其他非零参数的辨识结果。由于要避免这些零参数的辨识等原因，一般来说基于最小二乘原理的脉冲响应模型辨识采用的是多入单出的辨识模式。为方便采用多入单出辨识的模式，可将式（7-33）、式（7-34）表示为

其中，π_j表示所有与第j个依赖变量有动态因果关系的独立变量的指标集，（k-1）＝[Δw_i（k-1），Δw_i（k-2），…，Δw_i（k-N）]^T，，。

注解7.1 如果已知第i独立变量到第j依赖变量的时滞τ_ji，还可去掉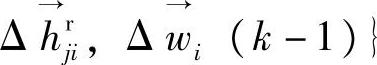的前τ_ji项，对此详略。

注解7.2 使用增量FIR模型可以降低阶跃型不可测扰动对辨识结果带来的不利影响，但对量测噪声ξ（k）是敏感的^[38]。上面给出的增量FIR模型是如下更为一般形式的简化表达：

如果Δξ（k）应该替换为ξ（k），即ARIX模型特例的情况，则担心增量法对量测噪声ξ（k）敏感就是多余的了。