全面评估功效：控制、观察、镇定、检测

模型的可镇定性（Stabilizability）和可检测性（Detectability）弱于其能控性（Controllability）与能观性（Observability）。

1.能控性

在控制理论中，能控性是模型的一个非常重要的性质，能控性在很多控制问题中起到了决定性的作用，例如不稳定模型的镇定。概略地说，能控性表征了控制输入对状态或输出的操纵能力。在实际应用中，能控性可拓广为状态能控性、输出能控性。

（1）状态能控性

状态是变量的集合，理想情况下完全地描述了系统的内部特征。状态能控性表征了控制输入对状态的转移能力，即在有限时间内将状态由任意初始状态转移到另一终端状态的能力。

考虑如下的离散时间线性时不变模型：

x（k+1）＝Ax（k）+Bu（k），y（k）＝Cx（k）+Du（k） （6-136）

其中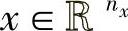，为状态；为输出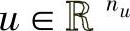；为控制输入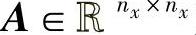；为状态矩阵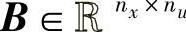；为输入矩阵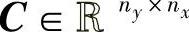；为输出矩阵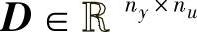；为传输矩阵。状态能控性的判定可以通过检验n_x×n_xn_u维矩阵

是否行满秩来实现，即判断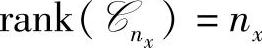。这就是说，如果状态是能控的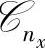，中将存在n_x个线性无关的列；如果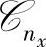中有n_x个列是线性无关的，则n_x个状态中的每一个都是能控的。

（2）输出能控性(www.xing528.com)

输出能控性表征了控制输入对输出的转移能力，即在有限时间内将输出由任意初始值转移到另一终端值的能力。状态能控模型不必输出能控，输出能控模型不必状态能控。对于模型式（6-136），当输出能控性矩阵

为行满秩（秩为n_y）时，模型为输出能控。

2.可镇定性

某些模型可能不满足能控性条件，此时可将模型的能控性要求弱化为可镇定性要求。当所有的不能控状态都是稳定的，则该模型是状态可镇定的。

3.能观性

能观性是表征根据外部输出重构内部状态的能力。如果模型式（6-136）的任意状态可以由一段时间的输出序列和控制输入序列唯一确定，则该模型是能观的。对模型式（6-136），如果能观性矩阵

的秩为n_x，则模型是能观的。基本原理在于如果矩阵有n_x个行是线性无关的，则n_x个状态中的每一个都可以通过输出和控制输入变量序列的线性组合观察到。

4.可检测性

某些模型可能不满足能观性条件，此时可将能观性要求弱化为可检测性要求。当且仅当一个模型中的所有不能观状态是稳定的，该模型是状态可检测的，简称可检测的。