将被控输出作为状态传递的关键步骤

在稳态工作点附近，系统的状态方程可以表示为如下的形式：

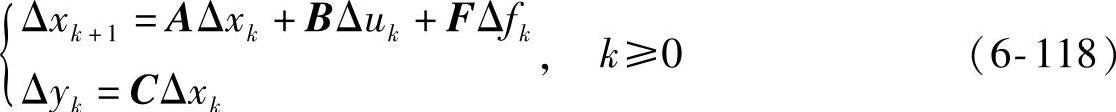
针对式（6-118），可用式（6-4）那样的模型，但由于模型中采用的是“Δx”或“Δy”，干扰d或p的稳态值将为零，除非系统含有积分模态。由式（6-118）得到Δy_k+1＝CΔx_k+1＝CAΔx_k+CBΔu_k+CFΔf_k。由于y_k+1＝y_k+Δy_k+1，可得到扩展形式的状态方程^[12]

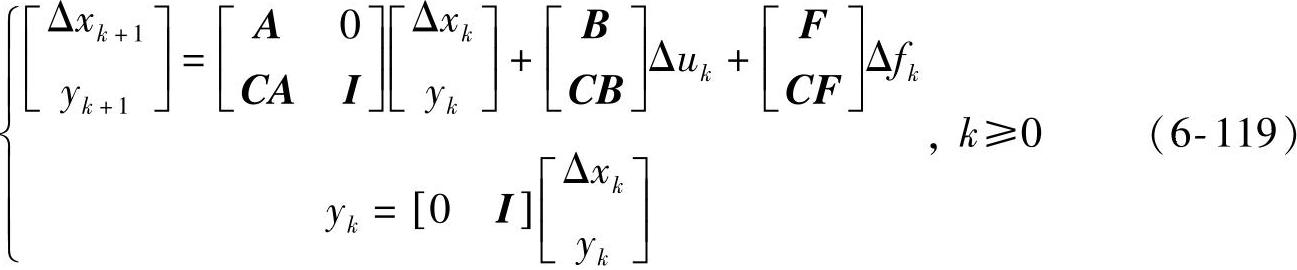
可以直接采用式（6-119）推导Kalman滤波、开环预测、稳态目标计算和动态控制，这是因为式（6-119）已经相当于在式（6-118）的基础上引入一个人工状态——尽管该人工状态是y_k，但也作为待估计的状态分量。

由于式（6-119）的输出方程相当于yk＝yk，故不适合再引入p。不妨在式（6-119）的基础上进一步引入d，得到如下带有人工干扰的状态空间模型描述：

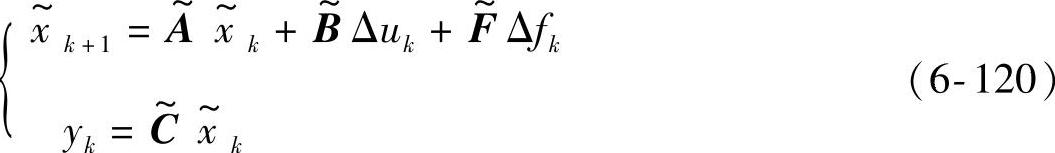
其中，增广的状态变量和系统矩阵为

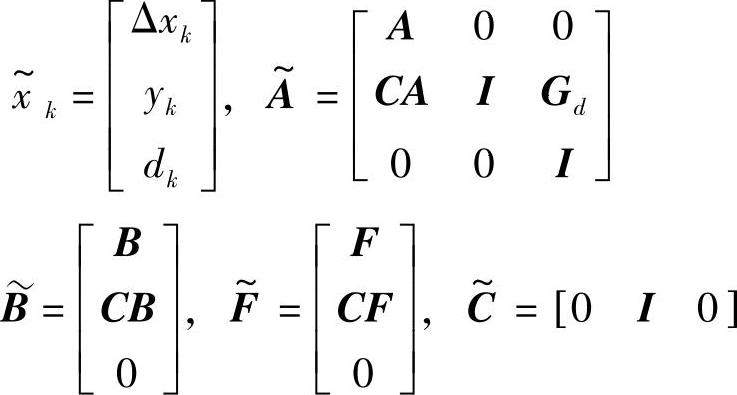
如果如下的秩条件满足：

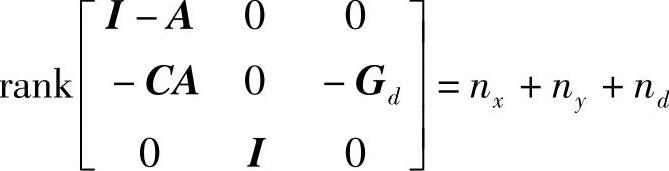
则可以采用式（6-120）推导Kalman滤波、开环预测、稳态目标计算和动态控制。

采用式（6-15）形式的Kalman滤波器，采用式（6-119）或者式（6-120）形式的状态空间模型，实际的闭环控制作用为式（6-98）。未来状态估计的开环预测值如下：

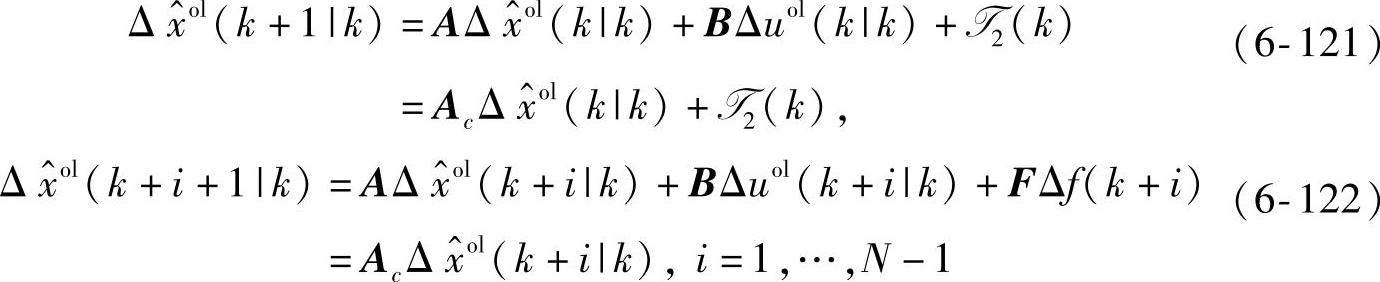
其中

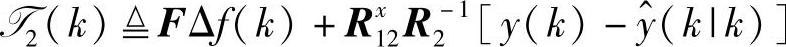(www.xing528.com)

预测初值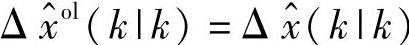。基于式（6-121）和式（6-122），未来输出和输入的开环预测值如下：

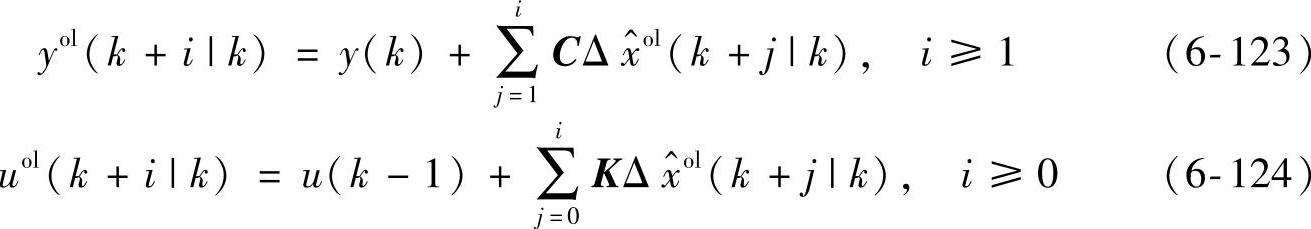
基于式（6-121）～式（6-124），得到开环稳态方程如下：

故继续的SSTC同6.3节。根据式（6-125）～式（6-127），在SSTC中，要得到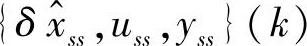，满足

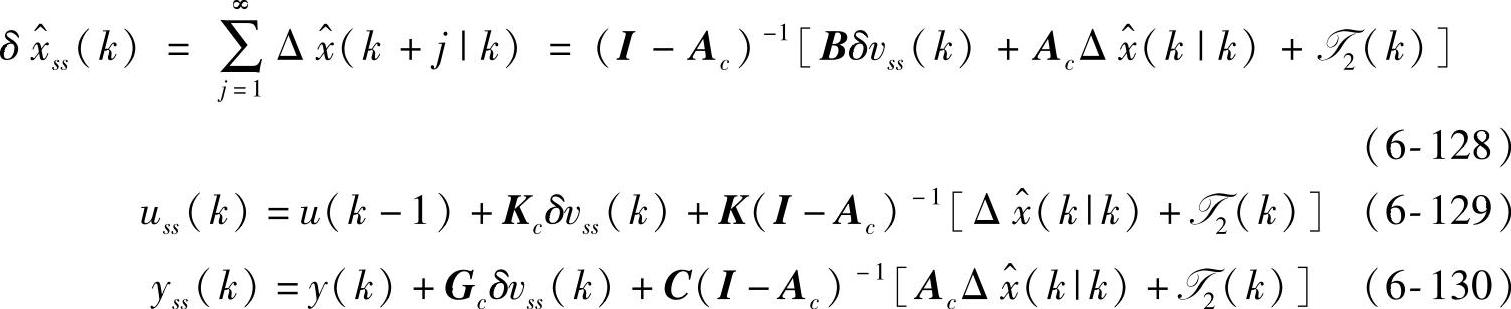
由式（6-129）减式（6-126）得到式（6-35），由式（6-130）减式（6-127）得到式（6-36）。

输出的闭环预测值如下：

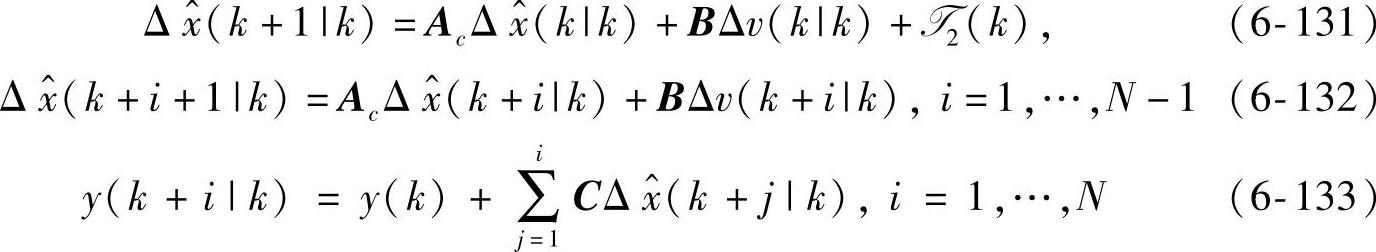
用式（6-131）减式（6-121）、式（6-132）减式（6-122）得式（6-116）。由式（6-116）迭代得式（6-117）。由式（6-133）、式（6-117）、式（6-123）得式（6-77）。将式（6-117）代入式（6-98）得式（6-85）。由式（6-85）得式（6-86），故继续的动态控制模块同6.4节。

例6.2 系统模型、模型失配和控制器参数见算例6.1。但是N＝20，N_c＝15。在k∈[62，76]时，出现值为f_eq+[0.6；-0.6]的干扰；k≥120时，出现值为f_eq+[-0.8；0.8]的干扰。控制结果见图6-2。

值得指出，在6.5.2节的算法中，由于采用增量模型，不管是否有模型失配，d的稳态值应该为零。

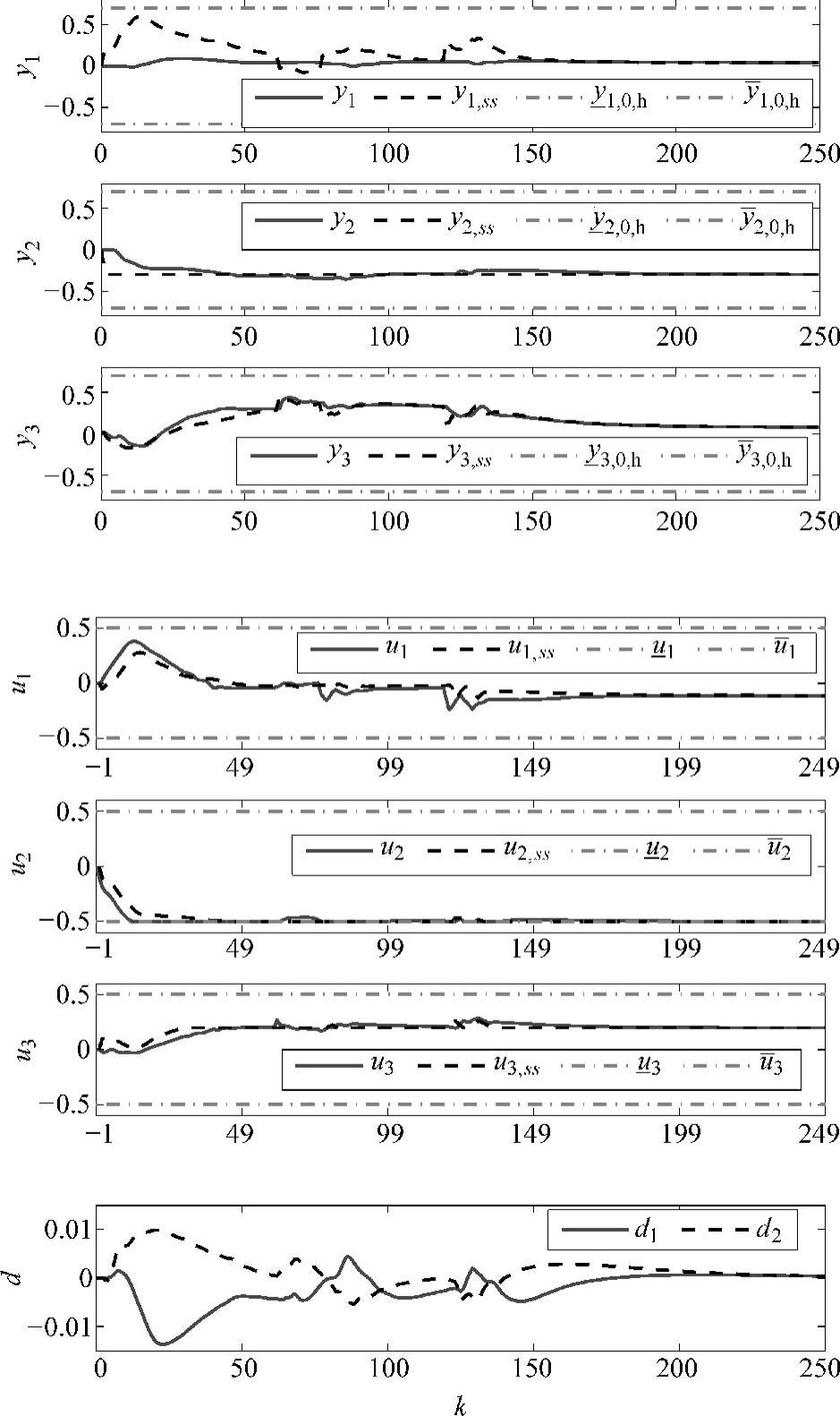
图6-2 控制效果图