动态控制模块的优化策略及实现

取控制时域为N_c，因此Δv（k+i|k）＝0，∀i≥N_c。基于Kalman预报方法，在当前和未来控制作用的影响下，输出的预测值如下：

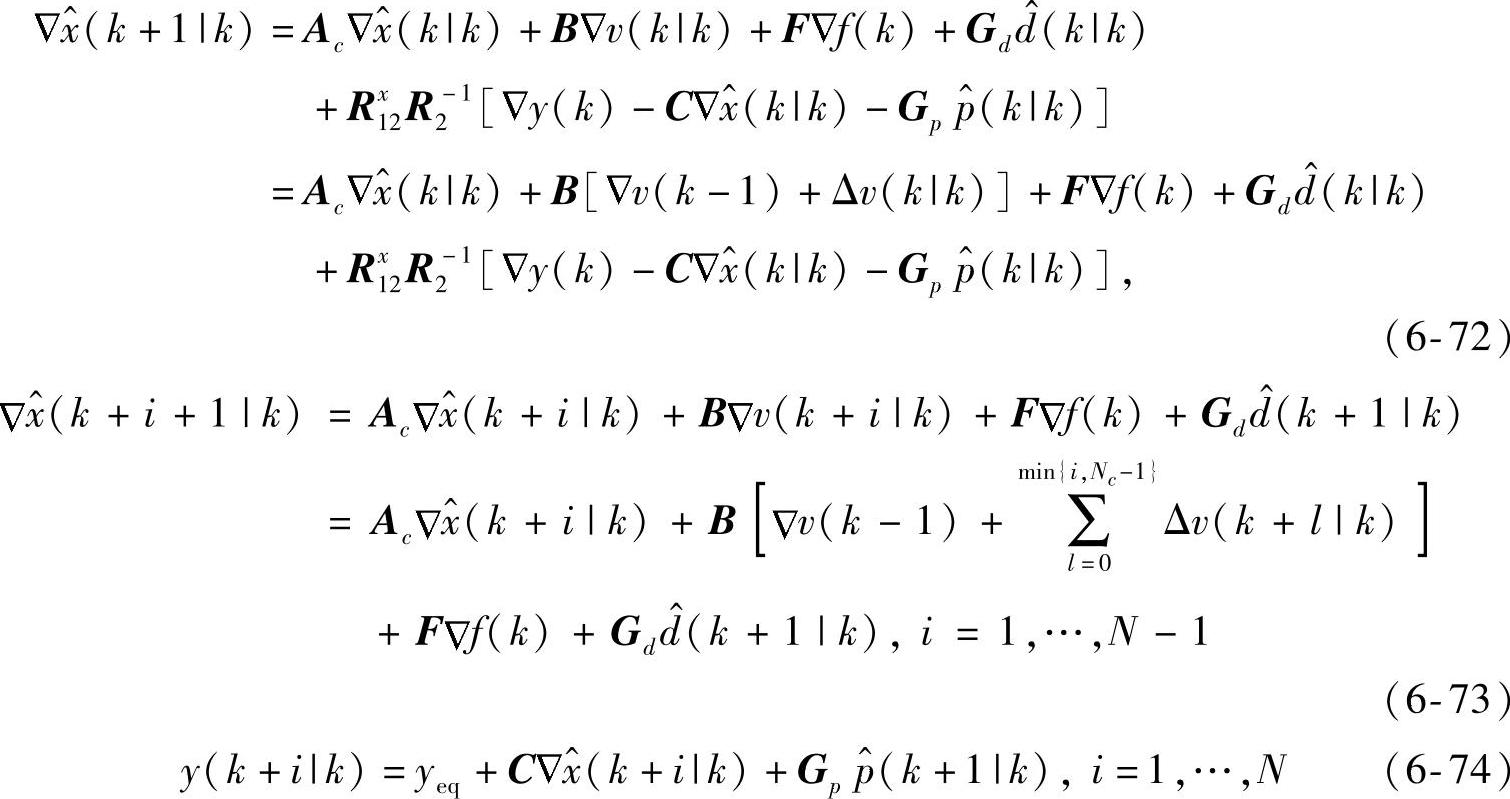
由式（6-72）减式（6-18）、式（6-73）减式（6-21）得

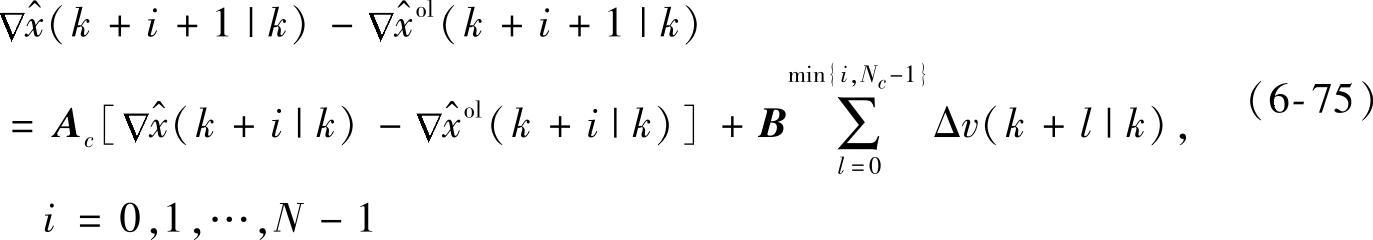
采用式（6-75）迭代得到

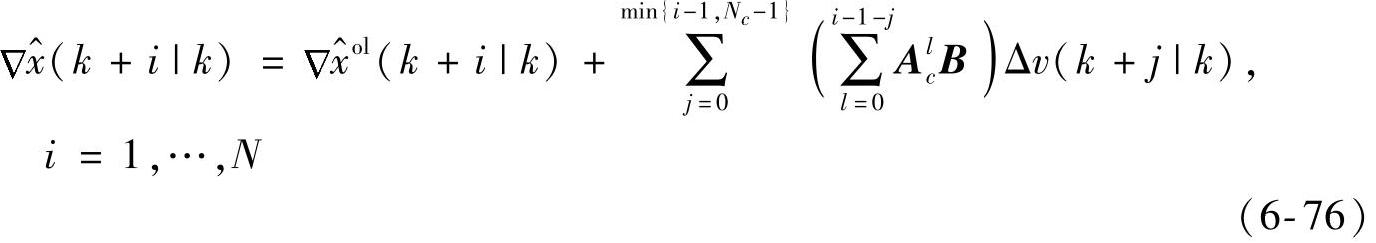
利用式{（6-74），（6-76），（6-22）}得到

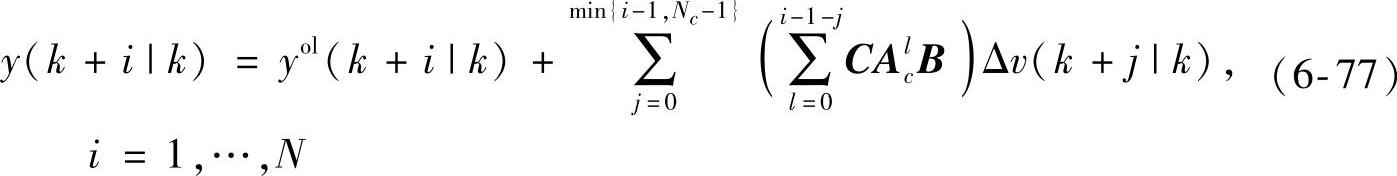
式（6-77）为闭环预测方程。

在动态控制中，假设要达到3个目的：①未来的输出尽量接近y_ss（k）；②抑制控制摄动的剧烈变化；③不可行时，通过放松输出软约束得到可行解。选择最小化如下的目标函数：

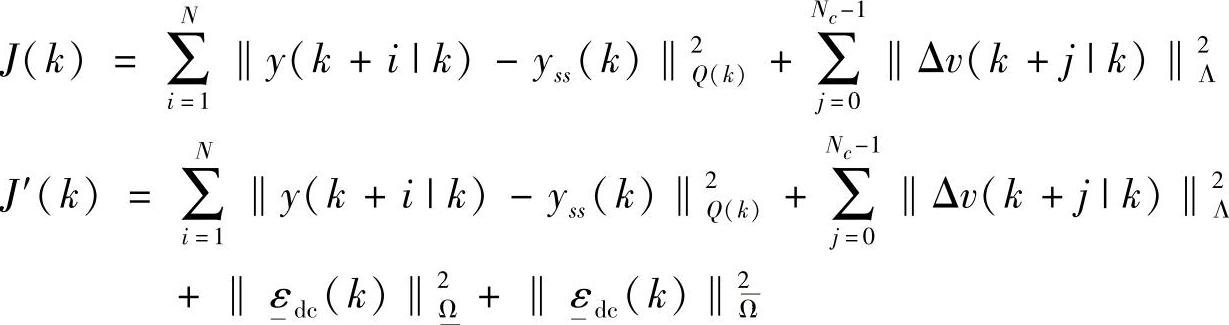
其中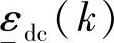，和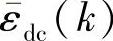为输出约束松弛量。目标函数中的加权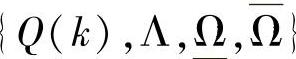同第4章（此处略）。

在动态控制中，通常考虑如下一些不等式约束（MV变化速率约束、MV幅值约束、CV幅值约束、松弛变量约束）：

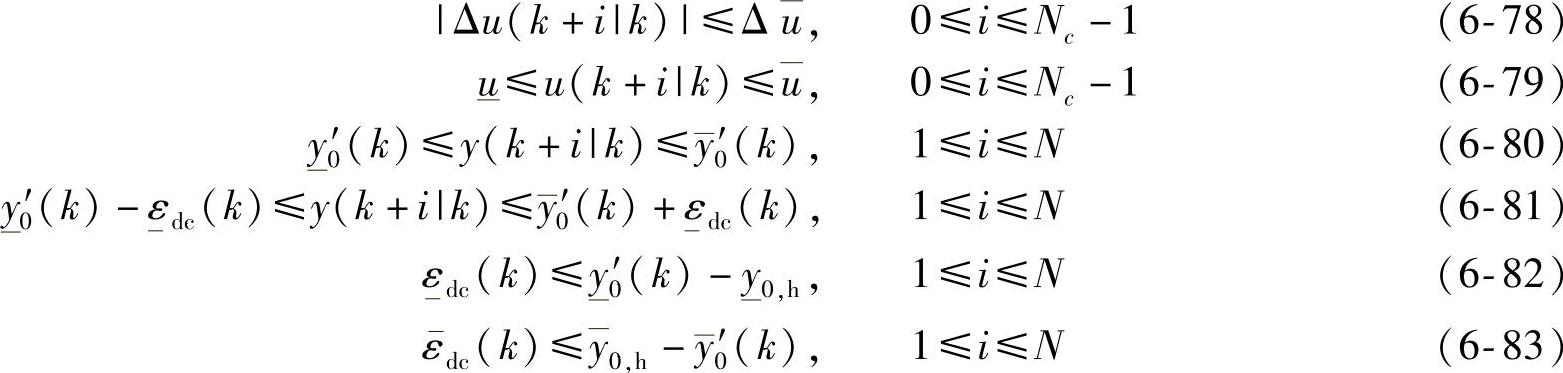
其中

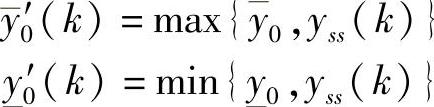
需要把以上约束式（6-78）～式（6-81）统一表示为关于Δv（k+l|k）（l＝1，…，N_c）的约束。由式（6-17）得到

其中后一个等式用到了

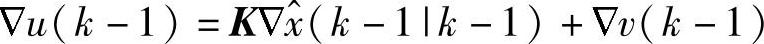
和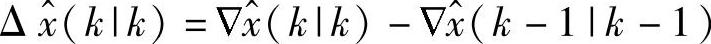。将式（6-76）代入式（6-17），并结合式（6-84）得到

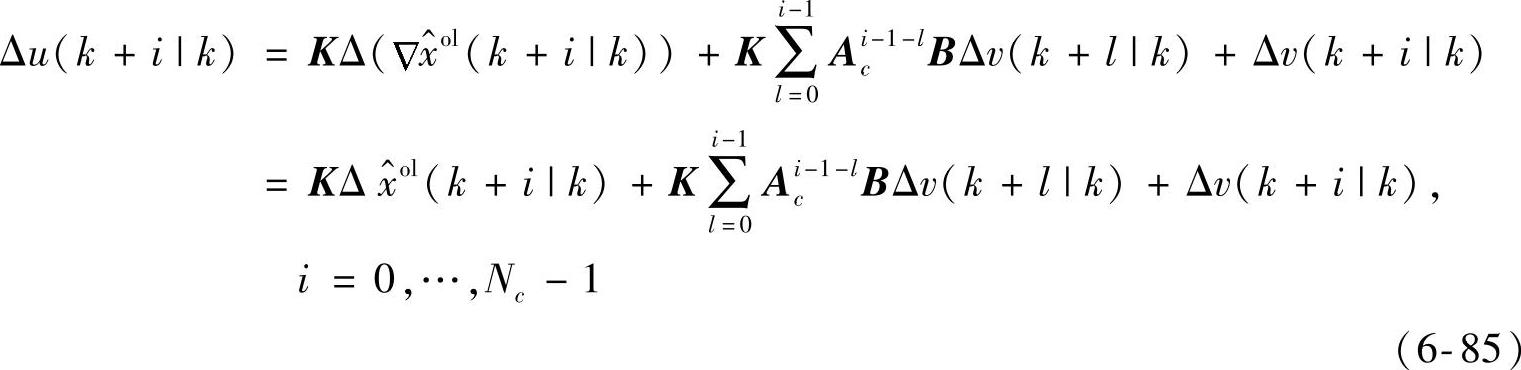
利用式（6-85）得到

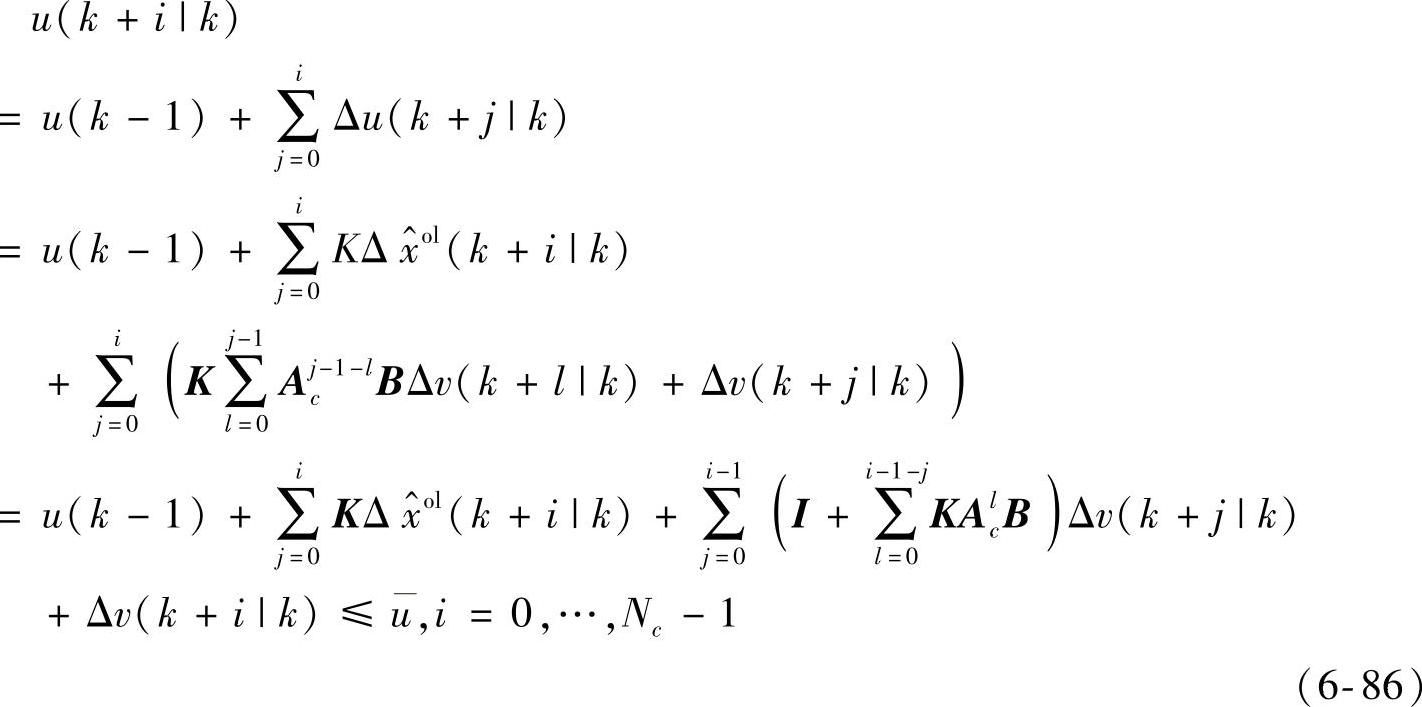
定义

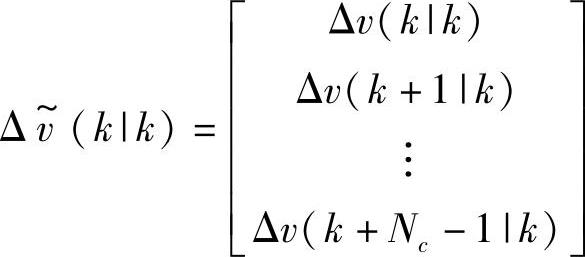
不同于对y_ss（k）的跟踪，对δv_ss（k）的跟踪通过在动态控制优化问题中加入如下的约束来实现：

其中，L＝[II…I]。

总之，在每个时刻k，首先求解优化问题

,s.t.式(6-78)～式(6-80)，式(6-87) (6-88)

如果式（6-88）不可行，则进一步求解

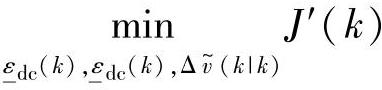，s．t.式(6-78)～式(6-79)，式(6-81)～式(6-83)，式(6-87) (6-89)

在求解以上两个优化问题时，将式（6-85）、式（6-86）、式（6-77）代入式（6-78）～式（6-81）。

优化问题式（6-88）～式（6-89）都可以采用标准的二次规划求解工具求解。由所得的解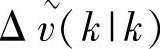，将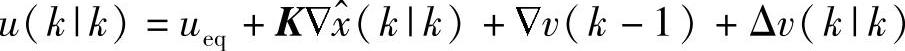送入实际被控系统。当然，由于执行结构的不准确性等原因，可能u（k）≠u（k|k）。

注解6.2 求A_c的高次幂可能导致数值计算问题，见参考文献[73]（第34页）。有的文献中，为了避免求A的幂，直接将输出或者状态预测值也当作决策变量^[40]。对本节方法，即采用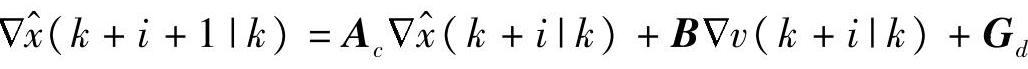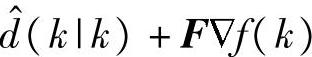，将该预测方程作为约束，将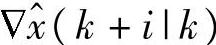和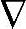v（k+i|k）都作为决策变量。

注解6.3 在目标函数中采用控制作用增量（此处为控制摄动增量），有利于消除CV余差，但实际上SSTC才是消除CV余差的关键^[25]。在双层MPC中，更重视消除CV跟踪稳态目标的余差。由于MV在大多数时候是PID控制器的设定值，其跟踪稳态目标的重要性低于CV的跟踪。

注解6.4 了解优化问题式（6-88）在去掉所有约束后的解析解是非常重要的。一般要求这个解析解存在且唯一，这等价于要求最小二乘问题的Hessian矩阵正定。假设Hessian矩阵可以表示成2（G^T_yQG_y+R）（其中Q和R分别由CV和控制摄动的加权系数组成），则取Q≥0，R＞0将确保Hessian矩阵正定。

例6.1 采用第3章提供的重油分馏塔模型，在平衡点附近，其连续时间传递函数矩阵如下：(www.xing528.com)

采样周期为4。采用第8章的开环子空间辨识方法得到状态空间模型，n_x＝20。取y_eq＝0、u_eq＝0和f_eq＝0。I_n表示n阶单位矩阵。

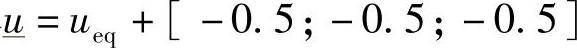
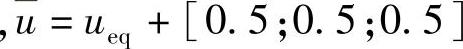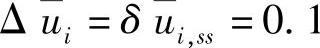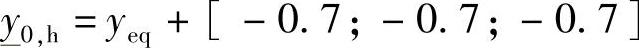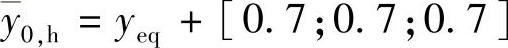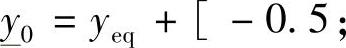
取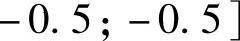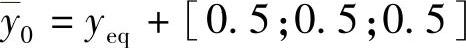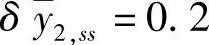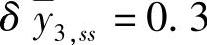，；，，，，，，，其中，y_1，ss、y_2，ss、u_3，ss具有外部目标并且其ET_range均为0.5。取R₁＝I₂₃，R₁₂的所有元素为0.1，R₂＝3I₃，由式（6-16）得到L。取Q_LQR＝I₂₀，R_LQR＝I₃，求解离散Riccati方程如下：

P_LQR＝Q_LQR+A^TP_LQRA-A^TP_LQRB（R_LQR+B^TP_LQRB）^-1B^TP_LQRA

并计算K＝-（R_LQR+B^TP_LQRB）^-1B^TP_LQRA。G_d＝[I₂，0]^T和G_p＝[1，0，0]^T。

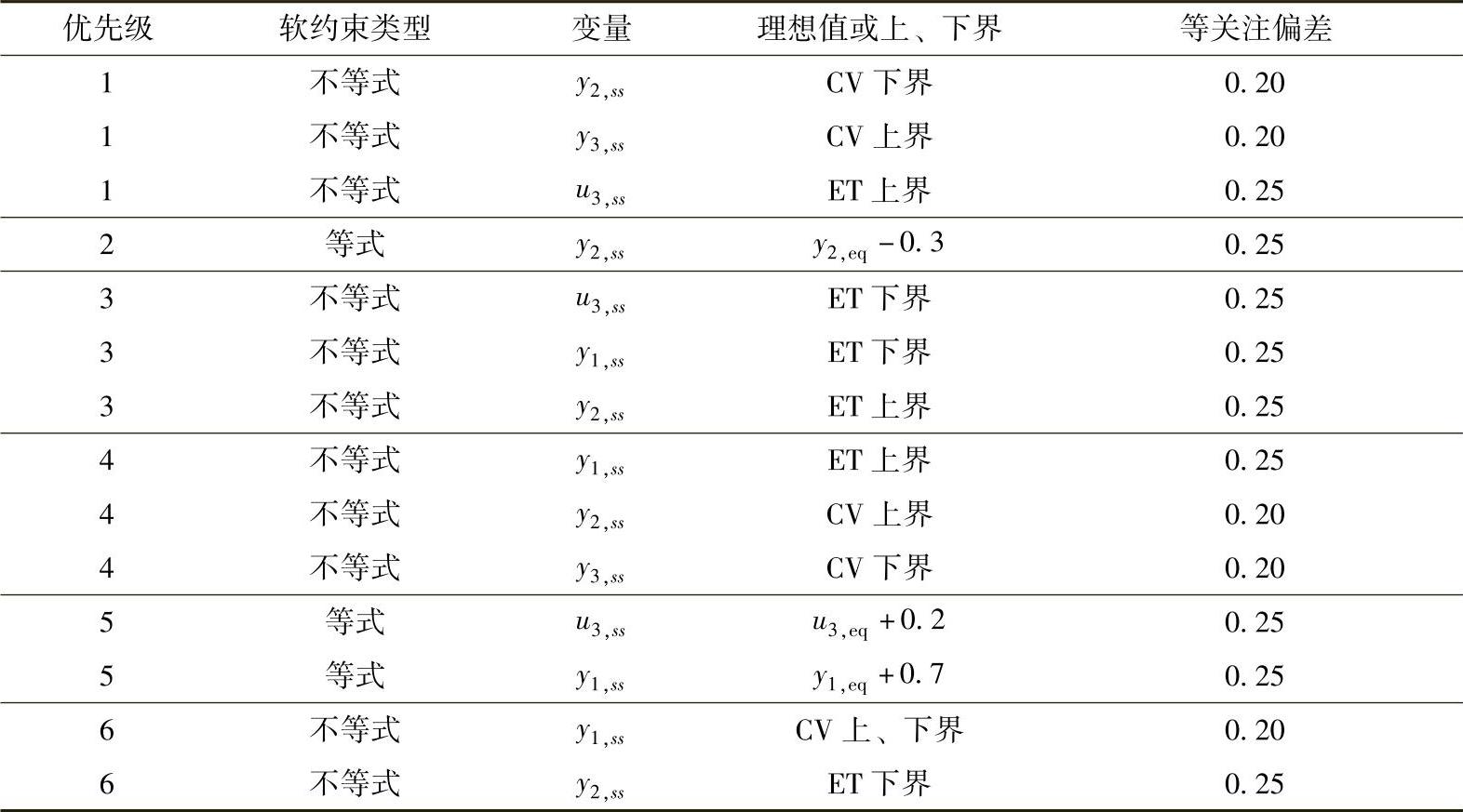
SSTC可行性阶段的相关参数设置见表6-1。取h＝[-2，-1，2]，无最小动作变量，J_min＝-0.4。在k∈[62，76]时，出现值为f_eq+[0.2；-0.1]的干扰；k≥120时，出现值为f_eq+[1；-1]的干扰。其他时段内干扰为f_eq。Y^ol_N（0|0）＝[y_eq；…；y_eq]。，u（-1）＝u_eq，y（0）＝y_eq。

表6-1 多优先级SSTC参数选取

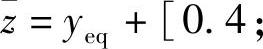
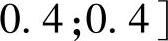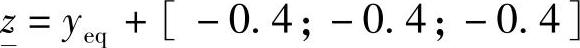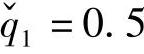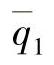动态控制器各参数选择如下：N＝15，N_c＝8，Λ＝diag{3，5，3}，，，＝2.0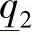，，＝2.0；＝2.0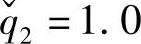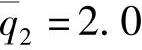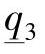，，；＝2.5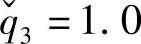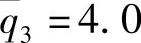，，，ρ＝0.2。u（k）＝u（k|k）。真实被控

对象为A_r＝0.9A，B_r＝0.9B，C_r＝0.9C，F_r＝0.9F。

下面采用线性规划，给出SSTC的所有优化问题，其中为方便没有对每个优先级的约束进行完全简化。

优先级1：

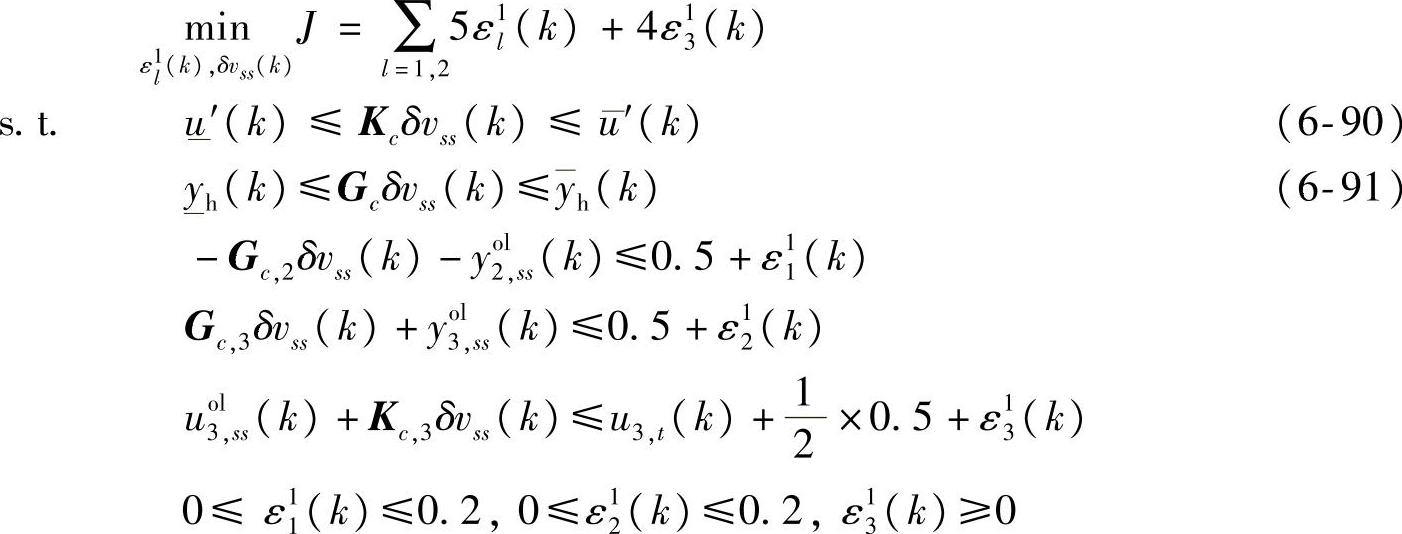
优先级2：

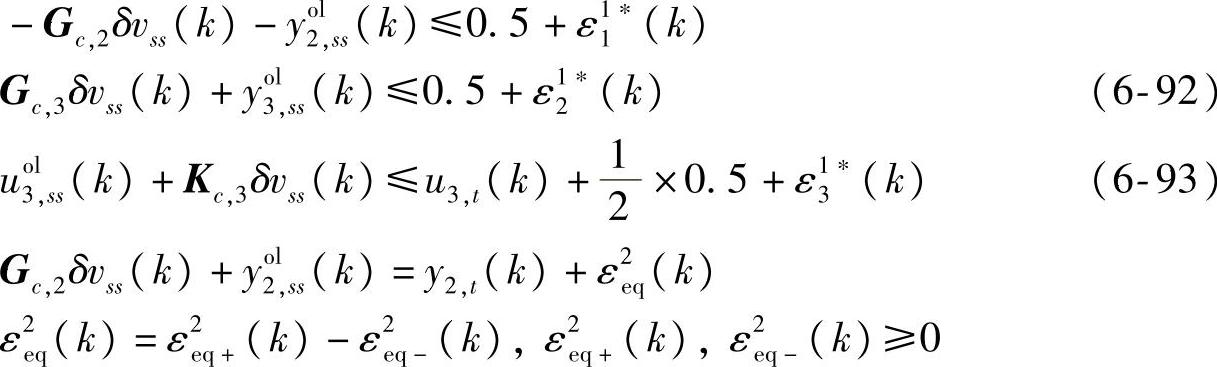
优先级3：

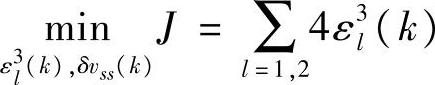
s.t.式（6-90）～式（6-93）

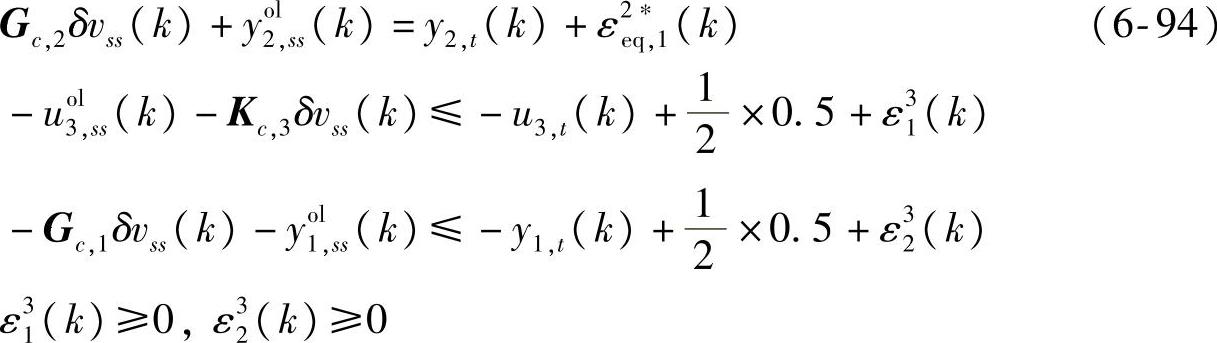
优先级4：

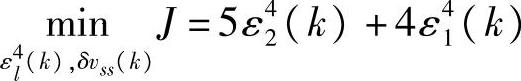
s.t.式（6-90）～式（6-94）

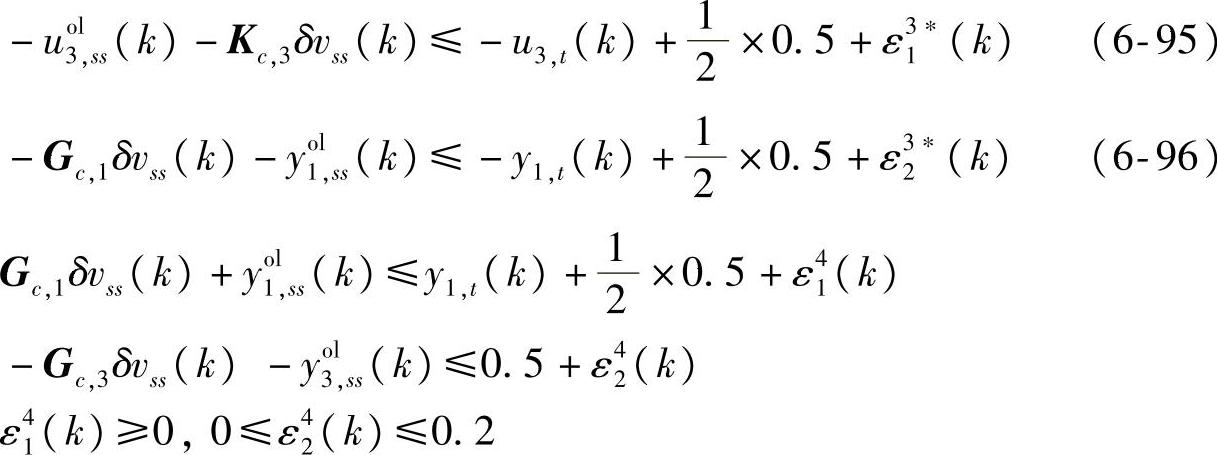
优先级5：

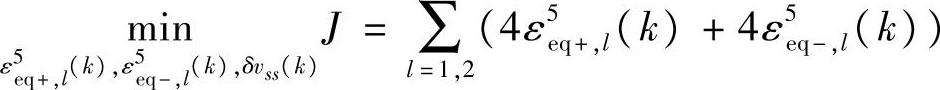
s.t.式（6-90）～式（6-96）

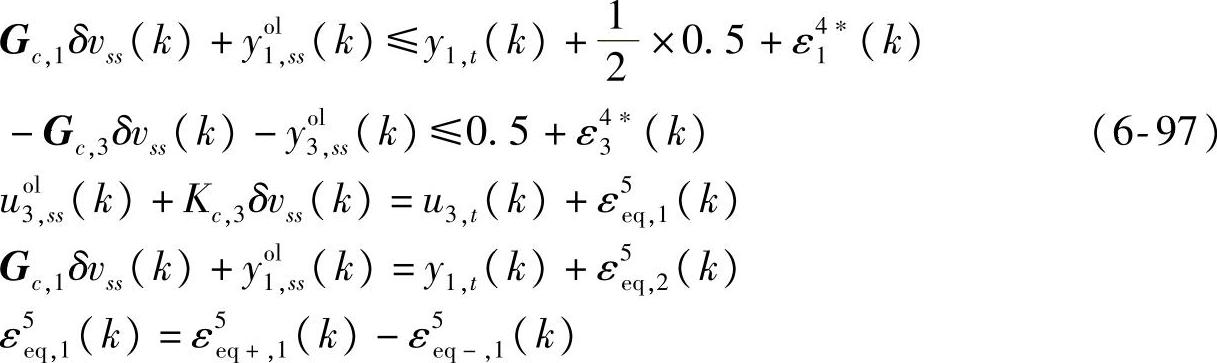
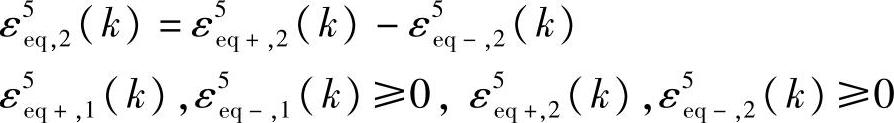
经济优化阶段：

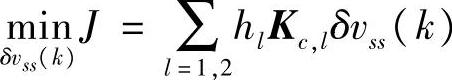
s.t.式（6-90）～式（6-92），式（6-94），式（6-97）

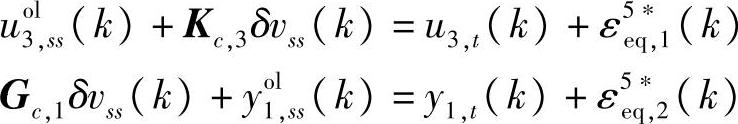
SSTC可行性阶段采用LP，经济优化阶段采用QP，动态控制结果见图6-1。

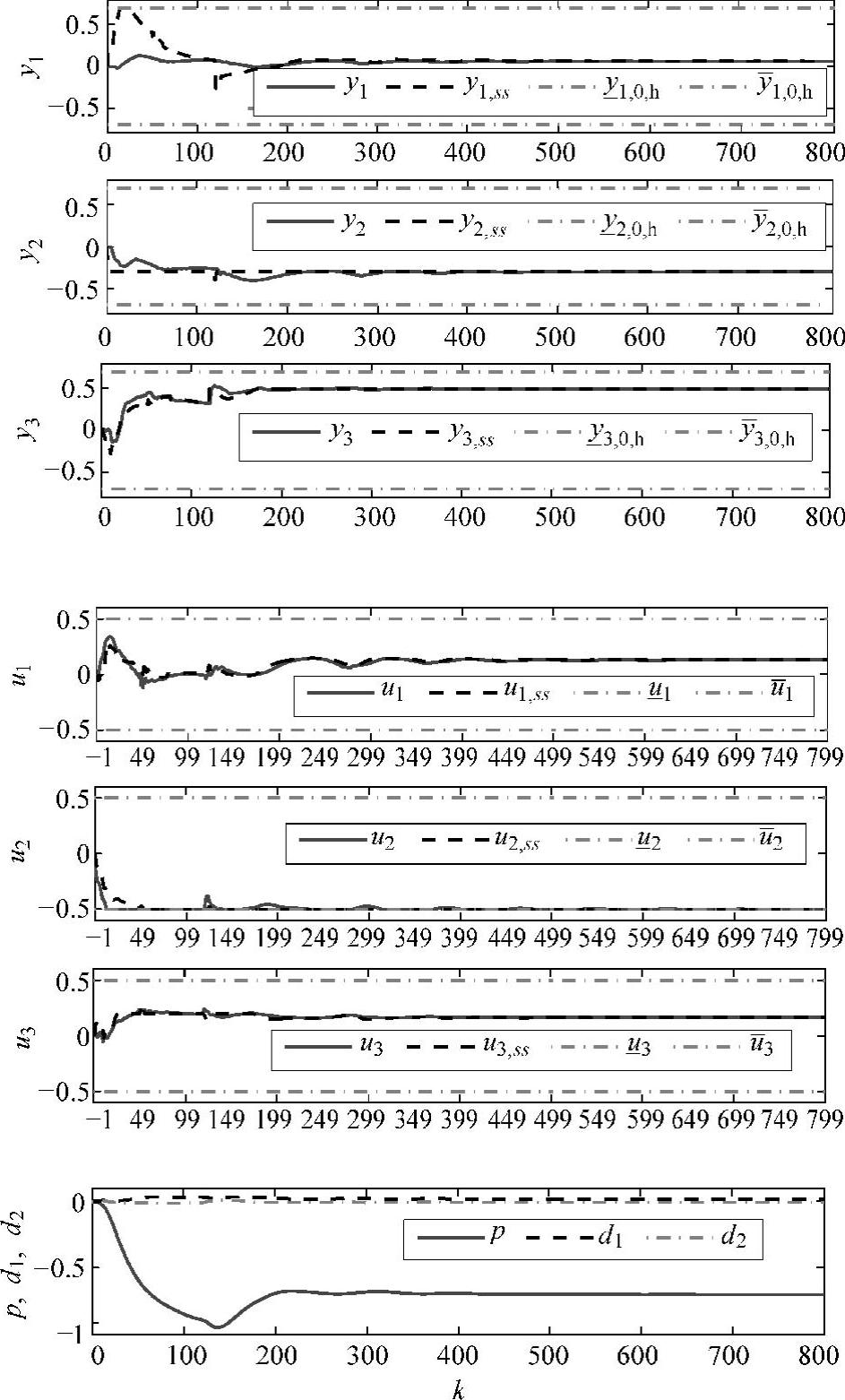
图6-1 控制效果图

注意在本算例中，取任意其他合适的平衡点[不需满足（I-A）x_eq＝Bu_eq+Ff_eq和y_eq＝Cx_eq]时，本章算法仍然可行。如果没有模型失配，且满足（I-A）x_eq＝Bu_eq+Ff_eq和y_eq＝Cx_eq，则平衡点的任意移动仅影响仿真中各变量的绝对数值，不影响相对值（曲线形状）。这些结果已经得到仿真验证，此处略。

另外，在本例中，如果将A替换为1.15A（即模型开环不稳定，有单位圆外特征值），而真实对象与模型一致，则适当调整参数后，系统仍可以镇定。经过一系列仿真，总结如下：系统可以不稳定，模型可以不准确。