开环预测模块对双层预测控制性能的关键作用

在双层结构预测控制中，利用增广状态空间模型式（6-4），得到扩展状态[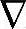x；d；p]的一步预报，其中干扰扩展状态[d；p]的一步预报作为实时稳态预测，而过程模型状态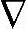x的一步预报作为开环动态预测的初值。显然，干扰扩展状态[d；p]的一步预报会影响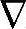x的开环预测的实时初值，从而影响过程模型的状态/输出的稳/动态预测值，这是通过干扰扩展状态[d；p]改进双层结构预测控制性能的关键所在。由于[d；p]在式（6-4）中引入了积分模态，且是不能控的，故不能利用式（6-4）的扩展状态[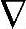x；d；p]直接进行反馈控制。相应地，在SSTC和动态控制的实施中，都不再涉及[d；p]的模型和估计值。

对式（6-4）～式（6-5）所示的增广模型，采用稳态Kalman滤波得到增广状态的估计如下：

状态滤波增益L被分解为过程模型状态滤波增益L_x、状态扰动滤波增益L_d以及输出扰动滤波增益L_p。求解如下代数Riccati方程（见第2章）：

得到解∑，从而可计算稳态Kalman滤波增益

其中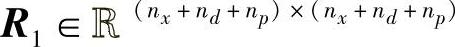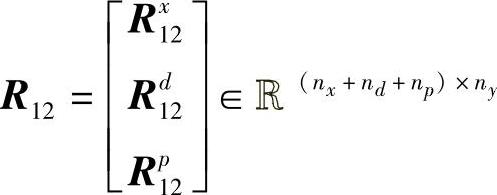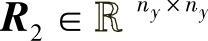，；；为可调参数，满足。

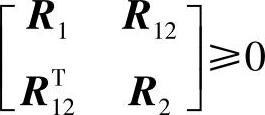若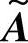中存在不能观模态，则不能观模态对应的特征值在转移阵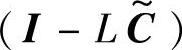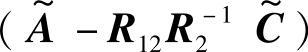中是不能被改变的。取R₁₂≠0时见假设2.5，以上稳态Kalman滤波器是在该假设下推导出的，而且相当于人为加入了对应于式（2-37）～式（2-38）的输入噪声和观测噪声。

如果模型式（6-1）不稳定，采用估计状态反馈控制律进行预镇定，实际的闭环控制作用为(www.xing528.com)

其中，K为控制器增益矩阵，使得A_c＝A+BK是渐近稳定的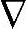，v为控制作用摄动项。定义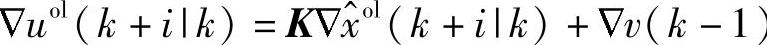为开环控制作用。所谓开环预测值，就是在开环控制作用下的未来值的估计。基于超前i≥1步稳态Kalman预报方法，未来状态估计的开环预测值如下：

其中，N为预测时域，上角标“ol”表示开环，预测初值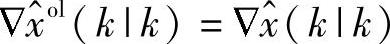。基于式（6-21），未来输出的开环预测值如下：

式（6-17）～式（6-22）为开环动态预测方程。

基于式（6-17）～式（6-22），得到开环稳态方程如下：

由于A_c是渐近稳定的，可以得到

其中，K_c＝K（I-A_c）^-1B+I，G_c＝C（I-A_c）^-1B为稳态增益矩阵。