积分型输出的扰动模型分析

考虑如下的针对SISO积分系统的增广模型：

其中含有输出阶跃干扰。令A＝1、B＝b、C＝c、G_d＝[]、G_p＝1，该模型具有式（6-4）～式（6-5）的形式。对定理6.2中的秩条件进行检验，可知

即增广模型式（6-10）不是可检测的。进一步考虑如下的增广模型：

其中含有输出阶跃干扰和状态干扰。对定理6.2中的秩条件进行检验，可知

即增广模型式（6-11）不是可检测的。

在DMC中，对积分型CV，将预测误差视为由恒值输出干扰和积分输出干扰共同组成。依据这个思路，SISO积分系统的增广模型可以表示为

由式（6-12）预测得到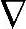y（k+j|k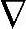）＝y′（k+j|k）+jcσs_k+s_k（j≥0），其中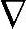y′（k+j|k）为与s_k无关的预测值。将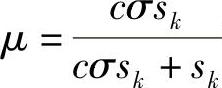称为旋转因子。由旋转因子得到σ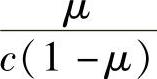＝。注意此处旋转因子的定义与第5章不同，但物理意义一致。第5章取σ∈[0，1]，而本章可以取σ∈（0，∞），故定义μ满足μ∈（0，1）。这种具有旋转因子的增广模型的一般形式为(www.xing528.com)

定理6.5 式（6-13）、式（6-14）中的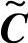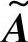（，）是可检测的，当且仅当（C，A）是可检测的且满足

该定理的证明基于式（6-6），细节见参考文献[36]。实际上，如果取

即可发现式（6-13）～式（6-14）所示的增广模型变为式（6-4）、式（6-5）所示的模型。如果取

其中，n_q＝n^r_y为积分模态的个数，即可发现式（6-13）～式（6-14）所示的增广模型同时包含了输出干扰、状态干扰和积分状态干扰。总之，式（6-13）～式（6-14）、定理6.5和式（6-4）～式（6-5）、定理6.2具有同样的一般性。

注解6.1 本节关于增广模型可检测性的结论，都是基于“（C，A）为可检测的”而得出的。由于干扰状态都是能观的，如果（C，A）是能观的，则本节增广模型的可检测性结论都能强化为能观性结论。