增广模型的可检测性优化方案

扰动模型设计的最基本目标是确保增广的干扰状态为可重构的。因为这些状态不是渐近稳定的，所以只有当增广模型式（6-4）～式（6-5）是可检测的，它们才是可重构的。我们将使用如下的方法来判别的可检测性，该方法的理论基础来自于Hautus定理（见参考文献[43]）的秩条件。

根据Hautus条件，增广模型式（6-4）～式（6-5）可检测的充要条件为

其中，为复数域。这里只需检查λ∈{1，λ^A_u}（其中λ^A_u={λ：λ=eig（A），∣λ∣≥1}为矩阵A的不稳定特征值）即可，因为这些是，∣λ∣≥1中唯一可能使式（6-6）中的矩阵降秩的情况。由式（6-6），可直接得到如下的结果。

引理6.1 当且仅当

时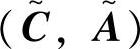，为可检测的。直接采用引理6.1判断的可检测性，在很多情况下并不容易，故接下来给出方便验证的可检测性定理。

定理6.2 式（6-4）、式（6-5）中的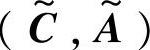是可检测的，当且仅当（C，A）是可检测的且满足

证明：基于引理6.1，下面分别证明该定理的充分性和必要性。

充分性[如果（C，A）是可检测的，且满足秩条件式（6-7），则增广模型是可检测的]：分两种情况考虑。

情况1（λ∈{λ^A_u}，λ≠1）：只有当d＝0时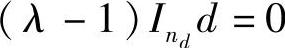，。只有当p＝0时，。由引理6.1可知，

唯一可能的解是[x；0；0]（x≠0）。由（C，A）的可检测性可知，不存在x≠0的解，使得当λ∈{λ^A_u}时，（λI-A）x＝0且Cx＝0。因此，由引理6.1可知，在这种情况下增广模型是可检测的。

情况2（λ＝1）：式（6-7）中的列满秩意味着

因此，根据引理6.1可知在这种情况下，增广模型是可检测的。

必要性[如果增广模型是可检测的，则（C，A）是可检测的且式（6-7）成立]：采用反证法，分两种情况考虑。

情况1[（C，A）不可检测]：存在一个λ∈{1，λ^A_u}和一个x≠0使得（λI-A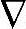）x＝0且C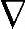x＝0。取该x并令d＝0和p＝0，由引理6.1可知增广模型是不可检测的。因此，（C，A）必须是可检测的。

情况2[式（6-7）不满足]：存在不全为0的x、d和p，使得（I-A）x-G_dd＝0且Cx+G_pp＝0。取这样的x、d和p并令λ＝1，由引理6.1可知，增广模型是不可检测的。因此，式（6-7）必须得到满足。

证毕

定理6.3 对于所有的可检测的（C，A），存在一个可检测的增广模型式（6-4）～式（6-5），其中，n_p+n_d＝n_y。

证明：解决该问题的出发点在于如何构造满足定理6.2的G_d和G_p。令n^r_y为积分模态（即A中值为1的特征值）的个数。分两种情况考虑。

情况1（n^r_y＝0）：选择任一满秩的，并移除G_d。因为n^r_y＝0，所以（I-A）满秩，（I-A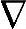）x＝0没有非零解。G_p满秩意味着G_pp＝0没有非零解。定理6.2的秩条件由此得到满足，所以增广模型是可检测的。

情况2（0＜n^r_y≤n，n_y，i≤n_y为线性无关输出的个数）：取矩阵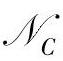，其列向量由矩阵C的零空间中的基向量组成。取满秩矩阵，使得rank（[（I-A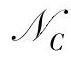），G_d]）-rank（[（I-A）]）＝n_y，i。取满秩矩阵使得[C，G_p]的秩为n_y。

（1）当n_y，i＝n_y时，式（6-7）中的列满秩意味着

由于（C，A）的可检测性意味着

故由G_d的秩条件可知式（6-9）成立。

（2）当n_y，i＜n_y时，由G_d的秩条件可知式（6-9）仍然是成立的。取不同时为零的x和d，使得（I-A）x-G_dd＝0，则由式（6-9）知Cx≠0。取这样的x，则由G_p的秩条件可知不存在使得Cx+G_pp＝0的扰动p。因此，定理6.2中的秩条件得到满足。(www.xing528.com)

证毕

定理6.3中G_d和G_p的构建算法说明了当扰动状态的个数等于输出的个数时可检测增广模型的存在性。接下来，将根据定理6.2得出一些有用的推论。但需注意，依据这些定理和推论给出的干扰模型，主要不是为了使式（6-4）可以更准确地描述实际系统，而是为了使闭环系统具有无静差控制的优点。实际上，最准确的干扰模型是与实际过程的干扰相匹配的模型。这些定理和推论只能提供建立干扰模型的基本准则。

推论6.4 满足如下条件之一时，式（6-4）、式（6-5）中的是不可检测的：

1）G_d不是列满秩；

2）G_p不是列满秩；

3）n_p+n_d＞n_y；

4）n_d超过线性无关输出的个数；

5）存在v_r≠0和p，使得（I-A）v_r＝0且G_pp＝-Cv_r；

满足如下条件之一时，式（6-4）～式（6-5）所示的增广系统是可检测的；

6）没有积分模态，（C，A）可检测，取G_p＝I和G_d＝[]；

7）输出线性无关，（C，A）可检测，取n_d＝n_y和n_p＝0，rank[（I-A）C，G_d]-rank[（I-A）C]＝n_d，

其中，C的列向量由矩阵C的零空间中的基向量组成。

证明：首先，1）～2）明显成立。

3）假设（C，A）是可检测的，G_d和G_p列满秩。如果状态干扰的总个数超过了输出的个数n_y，则

由于（C，A）是可检测的，则

可知存在不全为零的{x，d，p}，使得（I-A）x-G_dd＝0且Cx+G_pp＝0成立。因此，由定理6.2可知，增广模型是不可检测的。

4）假设G_d是列满秩的，令n_y，i为线性无关的输出的个数，满足n_y，i≤n_x和n_d≤n_x。如果n_y，i＝n_x，则n_d≤n_y，i，这不满足条件4），无需讨论。因此，假设n_y，i＜n_x，则存在矩阵C的一个非零零空间{v|Cv＝0}，其维数为n_x-n_y，i；进而因为G_d是列满秩的，故存在不全为零的{x，d}，使得C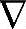x＝0和（I-A）x-G_dd＝0成立。显然，取这样的[x；d；0]，定理6.2的秩条件被违反，所以增广模型是不可检测的。

5）在推论条件下，令x＝v_r和d＝0，则由定理6.2可知增广模型是不可检测的。

6）由于A没有积分模态，则（I-A）是满秩的。余下的证明过程同定理6.3的情况1。这里不再赘述。

7）由于输出线性无关且n_y≤n_x，所以_C的秩为n_x-n_y同时G_d存在。余下的证明过程同定理6.3的情况2。这里不再赘述。

证毕

推论第5）条表明，工业应用中广泛使用的MPC默认的输出扰动模型G_p＝I并不适用于积分过程。推论第6）条表明，对于没有积分模态的过程模型，工业应用中广泛使用的MPC输出扰动模型是一个可检测的增广模型。推论第7）条表明，如果原始模型的输出是线性无关的，仅引入状态干扰就可以得到可检测的增广模型。