为了得到积分变量过程的数学模型,将第4章提供的重油分馏塔的数学模型进行了改造。这里,将y2改造为积分变量,相应的连续时间传递函数矩阵描述如下:

其中,MV包括u1、u2和u3;CV包括y1、y2和y3;DV包括f1和f2。取采样周期为1,模型时域N=300,采用MATLAB指令tfd2step,用以上传递函数矩阵得到式(5-1)所示的FSR模型(即得到分别针对u和f的阶跃响应系数矩阵Su,si、Su,ri、Sf,si和Sf,ri)。取yeq=0、ueq=0和feq=0。
在开环预测部分,积分旋转因子σ2=0.1,采用一阶惯性滤波,平滑系数α=0.5。取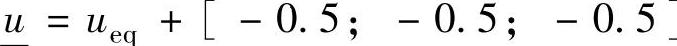 ,
,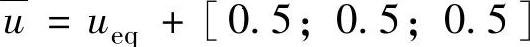 ,
,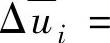
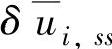 =0.2;
=0.2;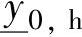 =yeq+[-0.7;-0.7;-0.7],
=yeq+[-0.7;-0.7;-0.7],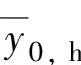 =yeq+[0.7;0.7;0.7],
=yeq+[0.7;0.7;0.7],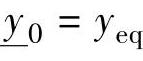 +[-0.5;-0.5;-0.5],
+[-0.5;-0.5;-0.5],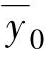 =yeq+[0.5;0.5;0.5],
=yeq+[0.5;0.5;0.5],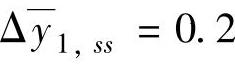 ,
,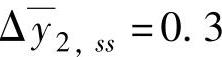 ,
,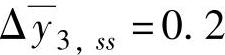 。y1,ss,y2,ss,u3,ss具有外部目标并且其ETrange均为0.5。对积分速率平衡方程、稳态速率约束、积分型CV平衡区和积分型CV设定值速率等,将在下面4个类型的积分CV中讨论。
。y1,ss,y2,ss,u3,ss具有外部目标并且其ETrange均为0.5。对积分速率平衡方程、稳态速率约束、积分型CV平衡区和积分型CV设定值速率等,将在下面4个类型的积分CV中讨论。
在SSTC中,关于软约束设置的相关参数,第Ⅰ、Ⅱ、Ⅳ类积分见表5-2,第Ⅲ、Ⅴ类积分见表5-3,均含最低优先级软约束。在经济优化阶段,u2为最小动作变量,h=[1,2,2]、Jmin=-0.2。在k≥99,有值为feq+[0.20;0.10]的干扰。Ys,olN(0|0)=[yseq;…;yseq],Yr,olN(0∣0)=[yreq;…;yreq]。
下面采用线性规划,以第Ⅰ类积分为例,给出SSTC的所有优化问题,其中为了书写简便,有些约束没有化简。优先级1:
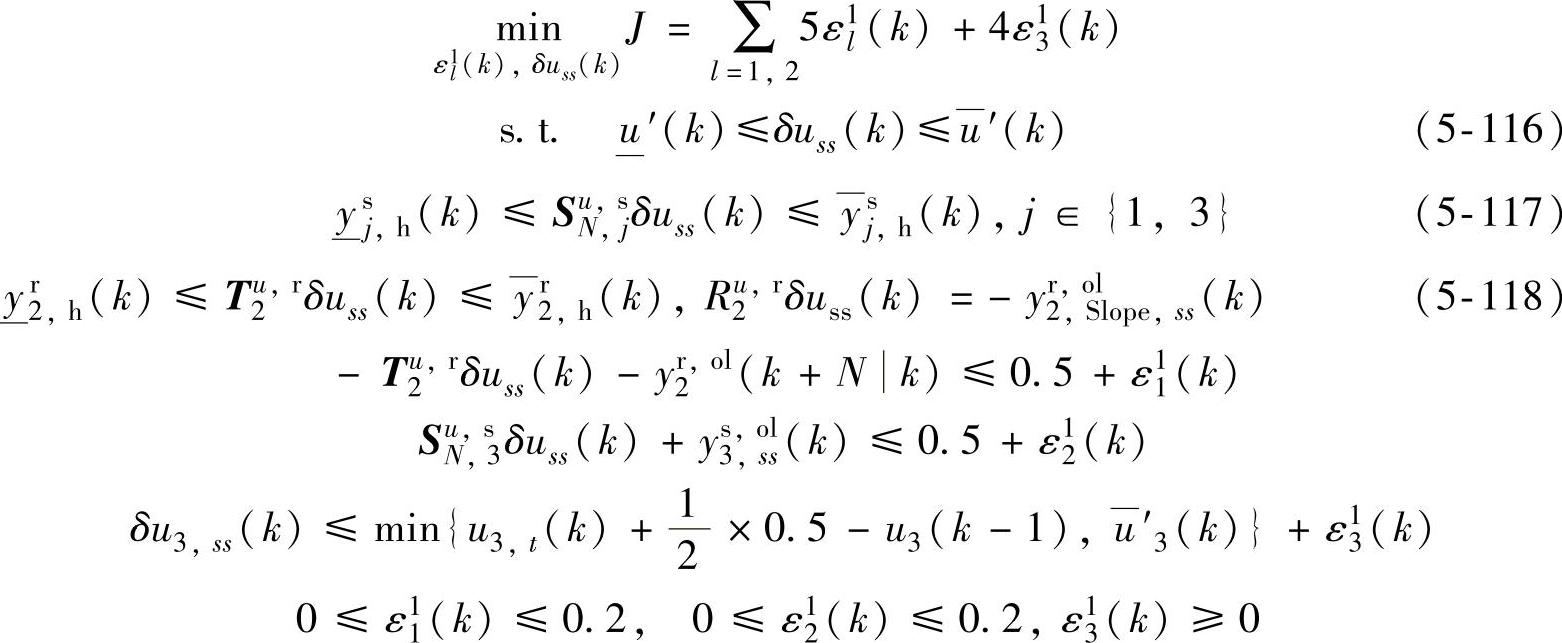
优先级2:
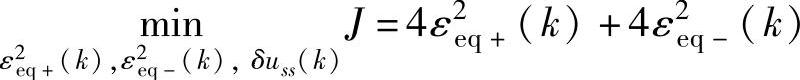
s.t.式(5-116)~式(5-118)
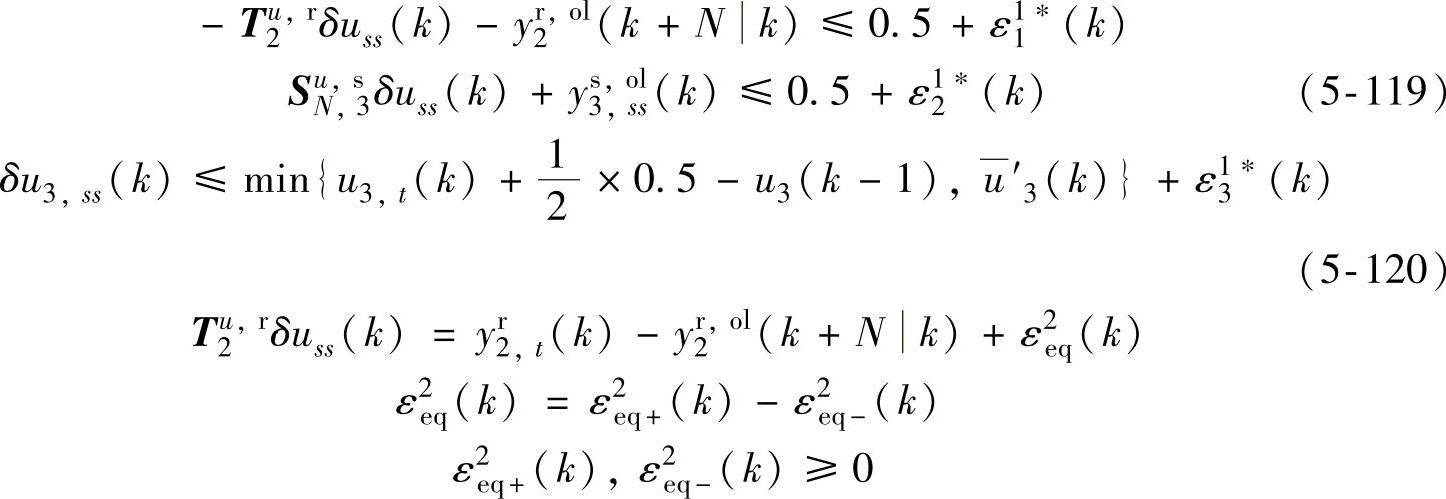
表5-2 多优先级SSTC参数选取(Ⅰ、Ⅱ、Ⅳ类积分)
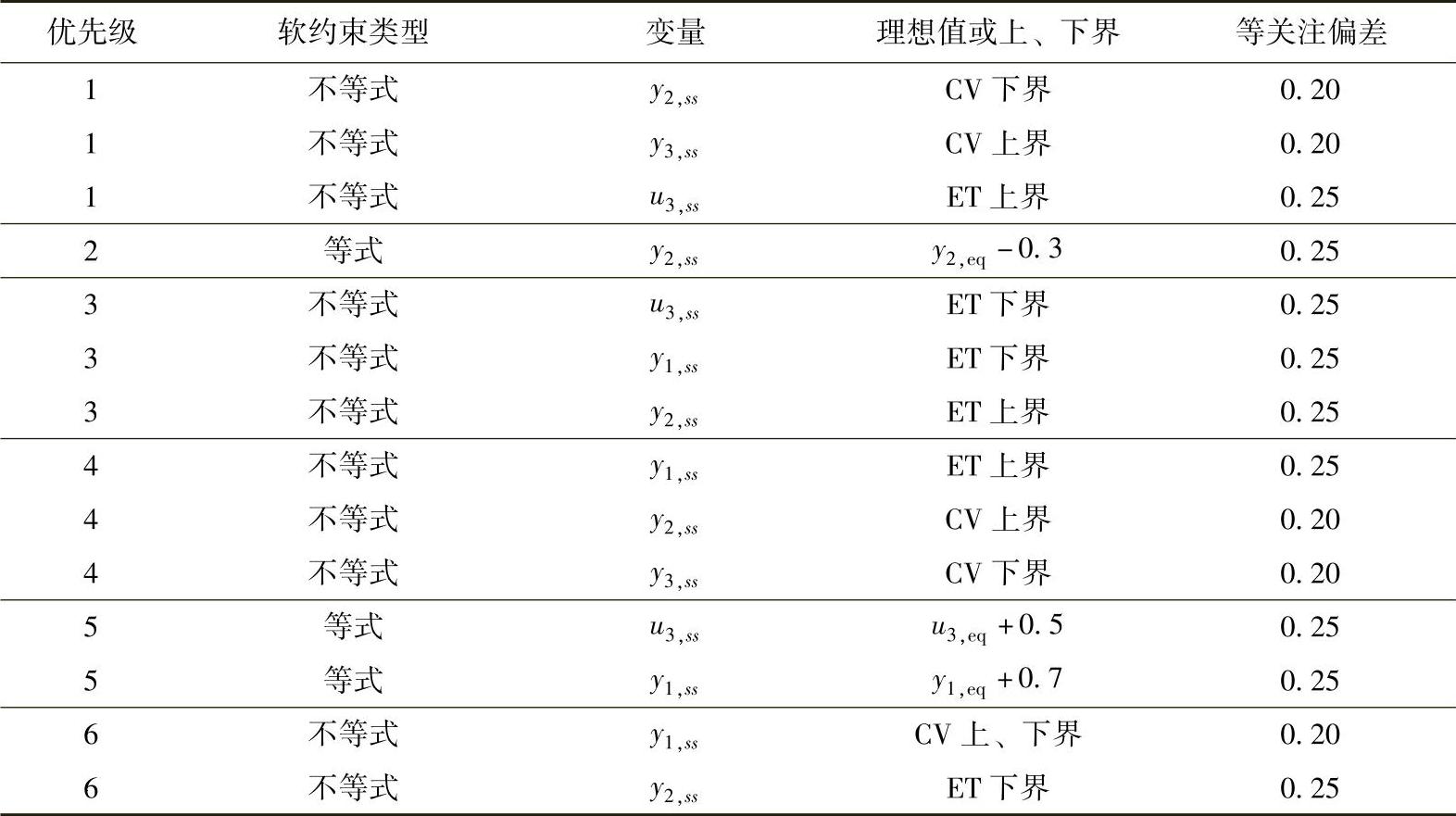
表5-3 多优先级SSTC参数选取(Ⅲ、Ⅴ类积分)
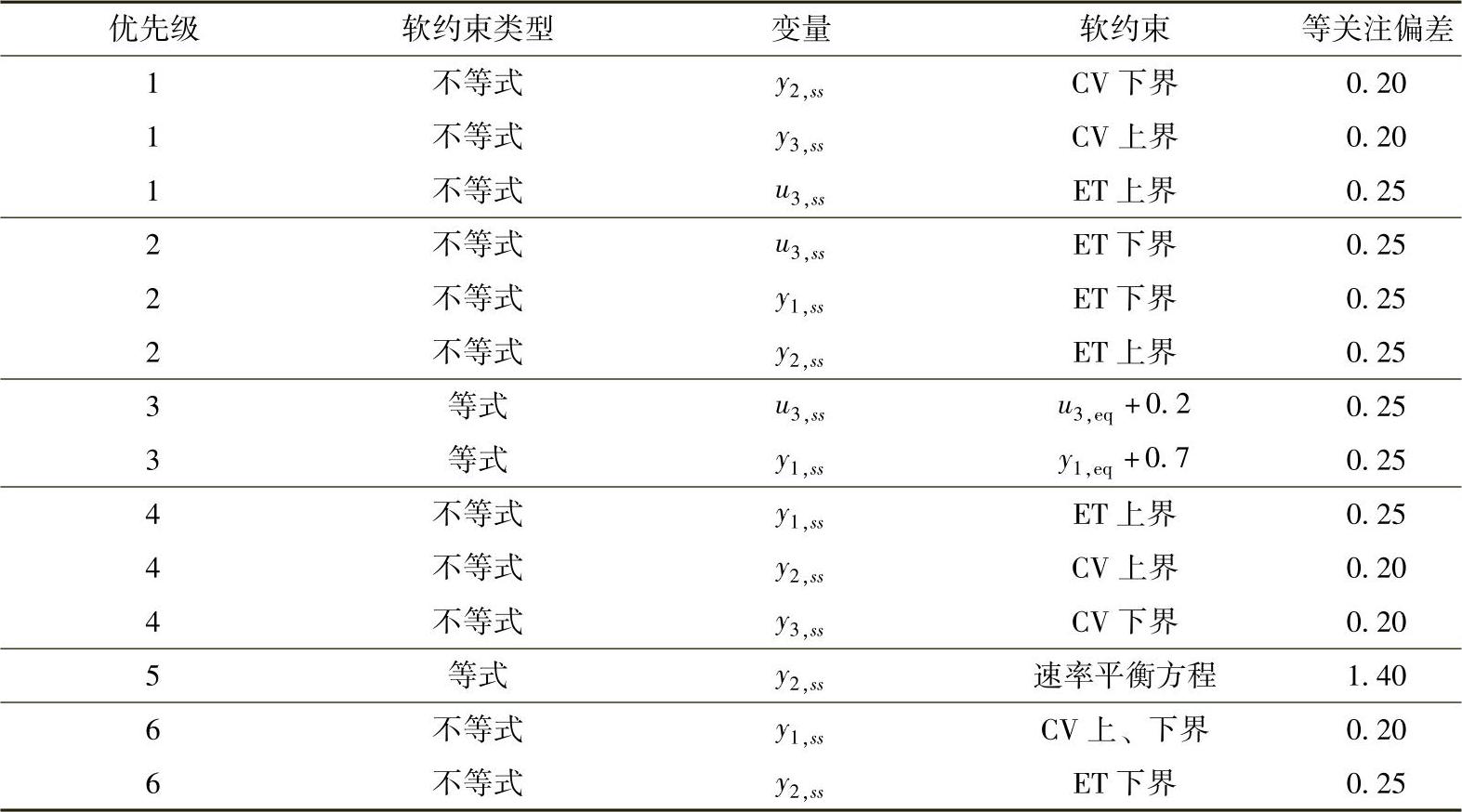
优先级3:
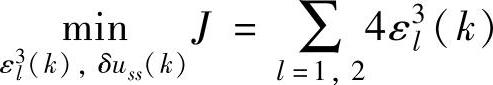
s.t.式(5-116)~式(5-120)
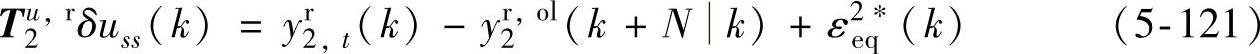
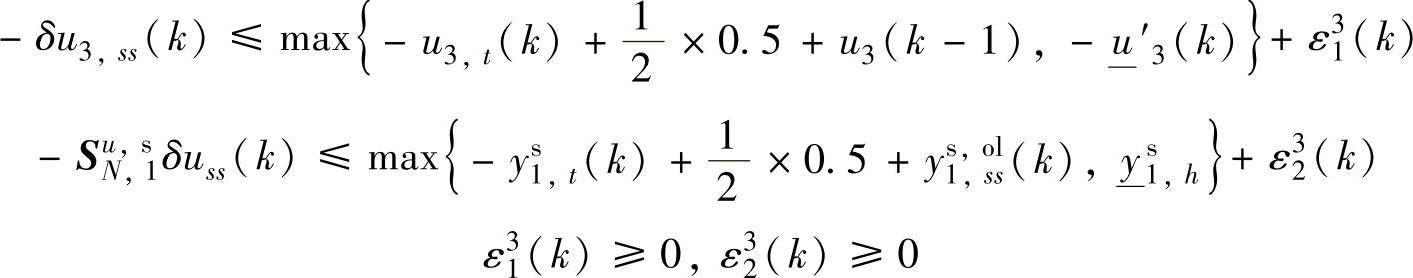
优先级4:
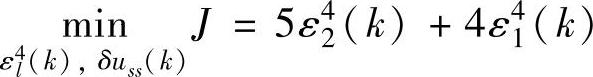
s.t.式(5-116)~式(5-121)
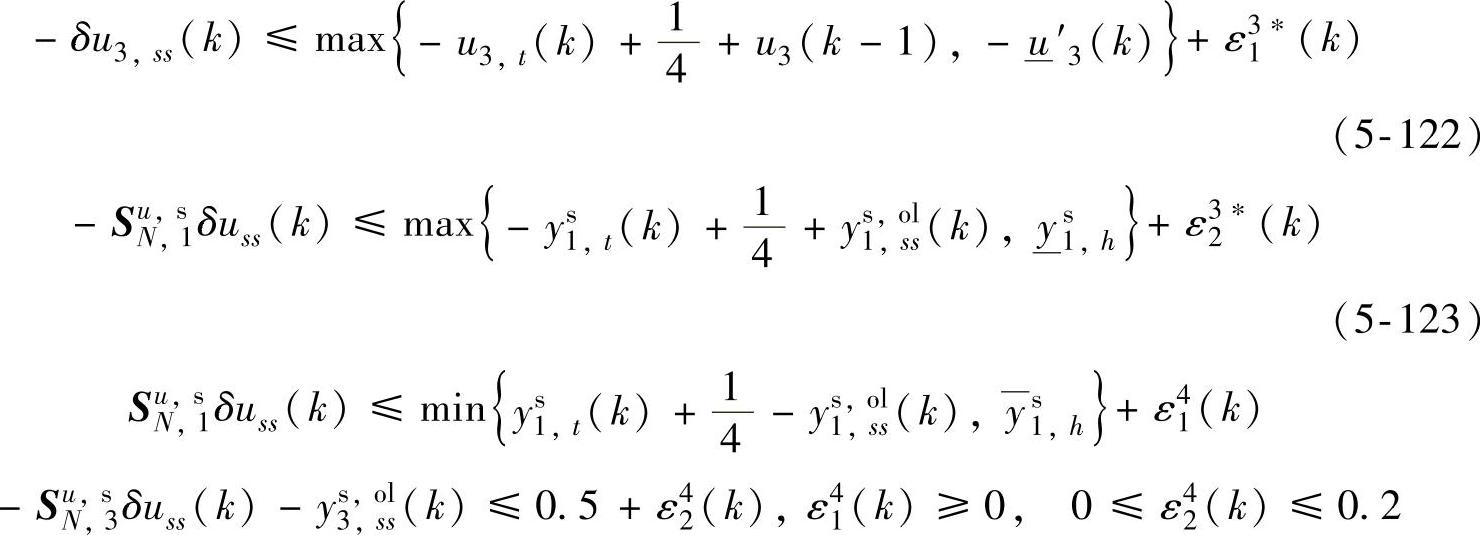
优先级5:
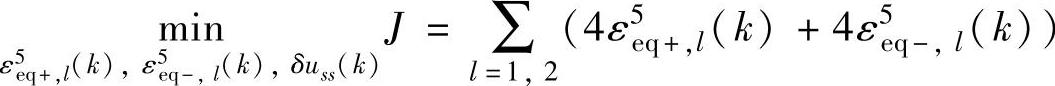
s.t.式(5-116)~式(5-123)
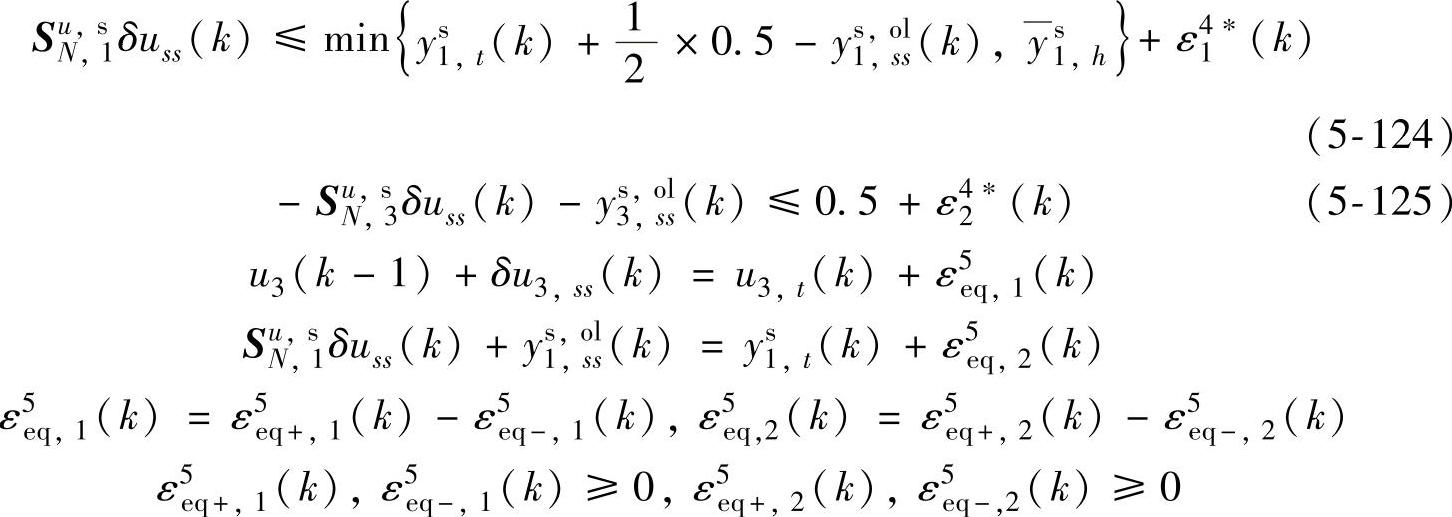
经济优化阶段(最低优先级软约束不起作用):
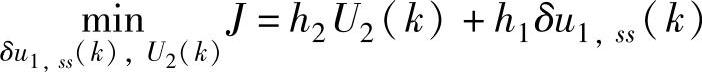
s.t.式(5-116)~式(5-119),式(5-121),式(5-125)
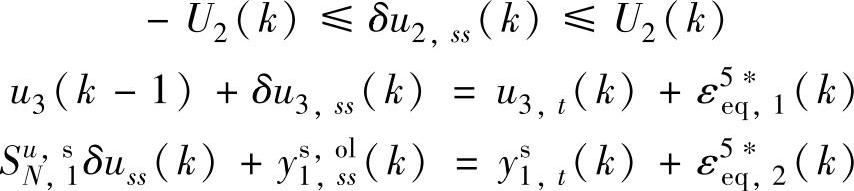
SSTC可行性阶段采用LP,经济优化阶段采用LP,获取稳态目标之后,采用动态控制模块来求取MV。动态控制部分的参数选择如下:P=15,M=8,Λ=diag{7,9,7},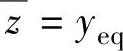 +[0.4;0.4;0.4],
+[0.4;0.4;0.4],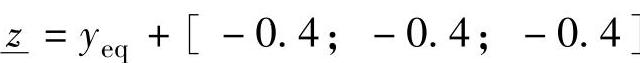 ,
,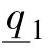 =2.0,
=2.0,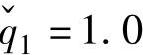 ,
,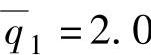 ;
;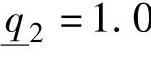 ,
,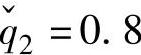 ;
;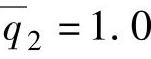 ;
;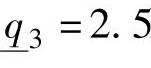 ,
,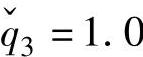 ,
,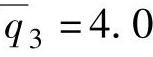 ,在进行
,在进行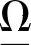 和
和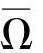 的确定时,参数ρ=1。初始值u(-1)=ueq,y(0)=yeq,而u(k)=u(k∣k)。真实系统输出用MATLAB和SIMULINK利用以上传递函数矩阵产生,并乘以0.9来代表模型与实际系统失配。
的确定时,参数ρ=1。初始值u(-1)=ueq,y(0)=yeq,而u(k)=u(k∣k)。真实系统输出用MATLAB和SIMULINK利用以上传递函数矩阵产生,并乘以0.9来代表模型与实际系统失配。
接下来针对不同类型的积分问题进行讨论。对不同类型的积分问题,以上各个优先级的约束会相应地改变。
1.第Ⅰ类积分问题,即y2为平衡经济型积分。取ξ2=1.25,则控制结果见图5-1。SSTC层给出的CV和MV的稳态值可以被动态控制层完全跟踪上。
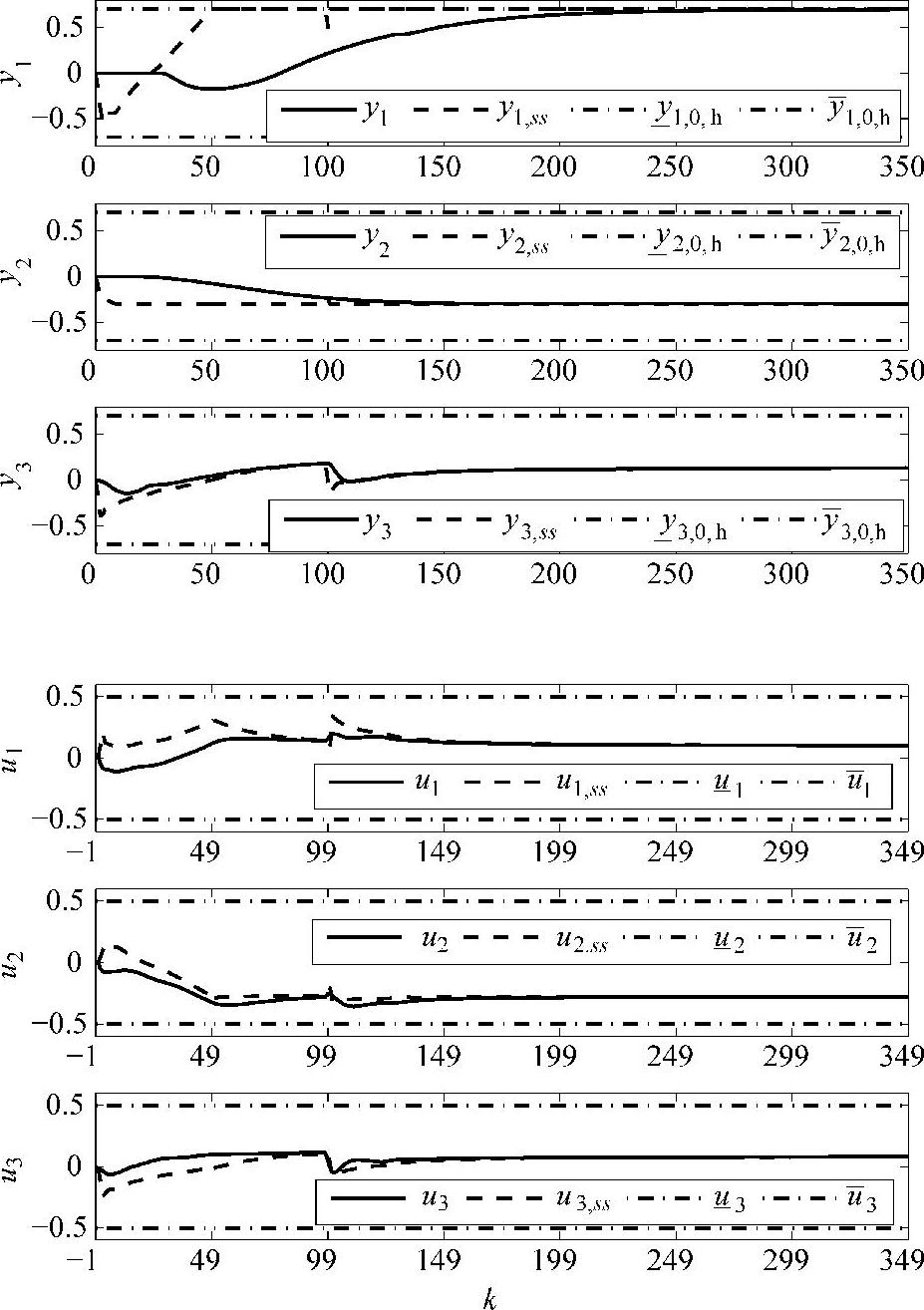
图5-1 第Ⅰ类积分控制效果图(https://www.xing528.com)
2.第Ⅱ类积分问题,即y2为失衡禁止型积分。外部设定值yr2,sp=y2,eq-0.3,积分型CV设定值速率κ2=0.5,则控制结果见图5-2。
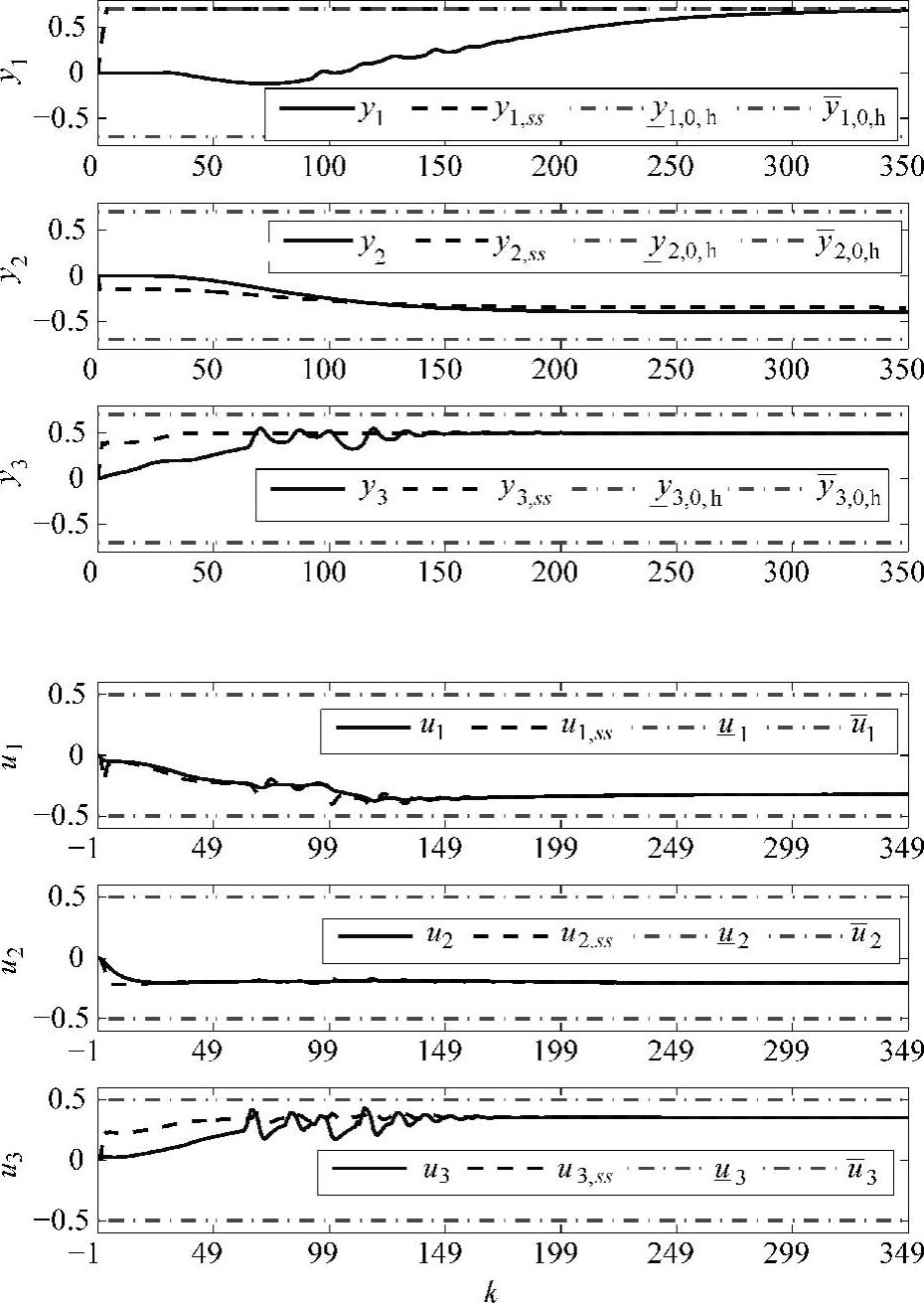
图5-2 第Ⅱ类积分控制效果图
从图5-2中可以看出,y2在跟踪yr2,ss时的响应速度非常慢,这与积分CV的处理方法和参数设置都有关系。改变动态控制模块的一些参数,如下: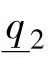 =50,
=50,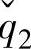 =40,
=40,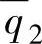 =50,则控制结果见图5-3,可以看出SSTC层给出的CV和MV的稳态值可以被动态控制层完全跟踪上,并且达到了给定的CV的外部设定值yr2,sp。
=50,则控制结果见图5-3,可以看出SSTC层给出的CV和MV的稳态值可以被动态控制层完全跟踪上,并且达到了给定的CV的外部设定值yr2,sp。
3.第Ⅲ类积分问题,即y2为期望平衡型积分。设置积分型CV安全时域L=200,外部设定值yr2,sp=y2,eq-0.3,设定值速率κ2=0.5,连续失衡最大容许次数Mib=5,平衡区为[y2,eq-0.5,y2,eq-0.4]和[y2,eq+0.4,y2,eq+0.5]。因为这里需要将式(5-23)作为软约束,故对SSTC的设置与Ⅰ、Ⅱ类积分不同。
每个优先级的优化问题这里不再赘述。控制结果见图5-4。第Ⅱ类积分问题将式(5-23)作为硬约束,在整个过程中式(5-23)始终满足;而在本类积分问题中,将式(5-23)作为软约束,在仿真过程中既存在满足式(5-23)的情况,又存在不满足式(5-23)(即被放松)的情况。观察图5-4和图5-2,可以发现图5-4中的控制曲线相对更加平滑。
与图5-2类似,图5-4中的仿真结果出现了y2缓慢跟踪yr2,ss的情况,其原因同上。
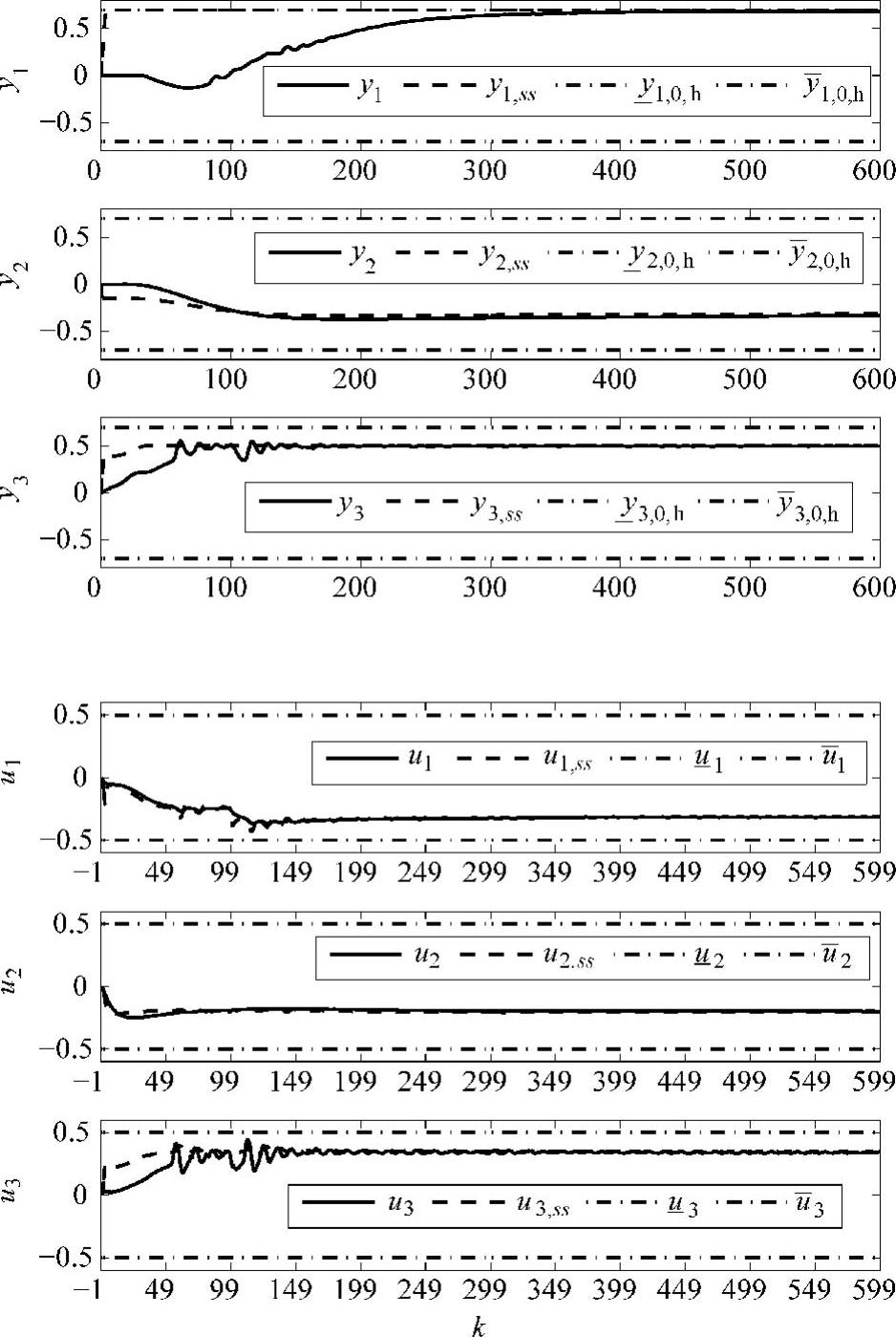
图5-3 第Ⅱ类积分控制效果图(q2=50, ,
,
4.第Ⅳ类积分问题,即y2为失衡允许型积分。设置积分型CV安全时域、外部设定值、设定值速率、连续失衡最大容许次数、平衡区同第Ⅲ类积分问题。
动态控制结果见图5-5,y2的变化是一个平缓的过程,满足式(5-31)的硬约束,并最终趋于平稳。SSTC层给出的CV和MV的稳态值可以被动态控制层完全跟踪上。
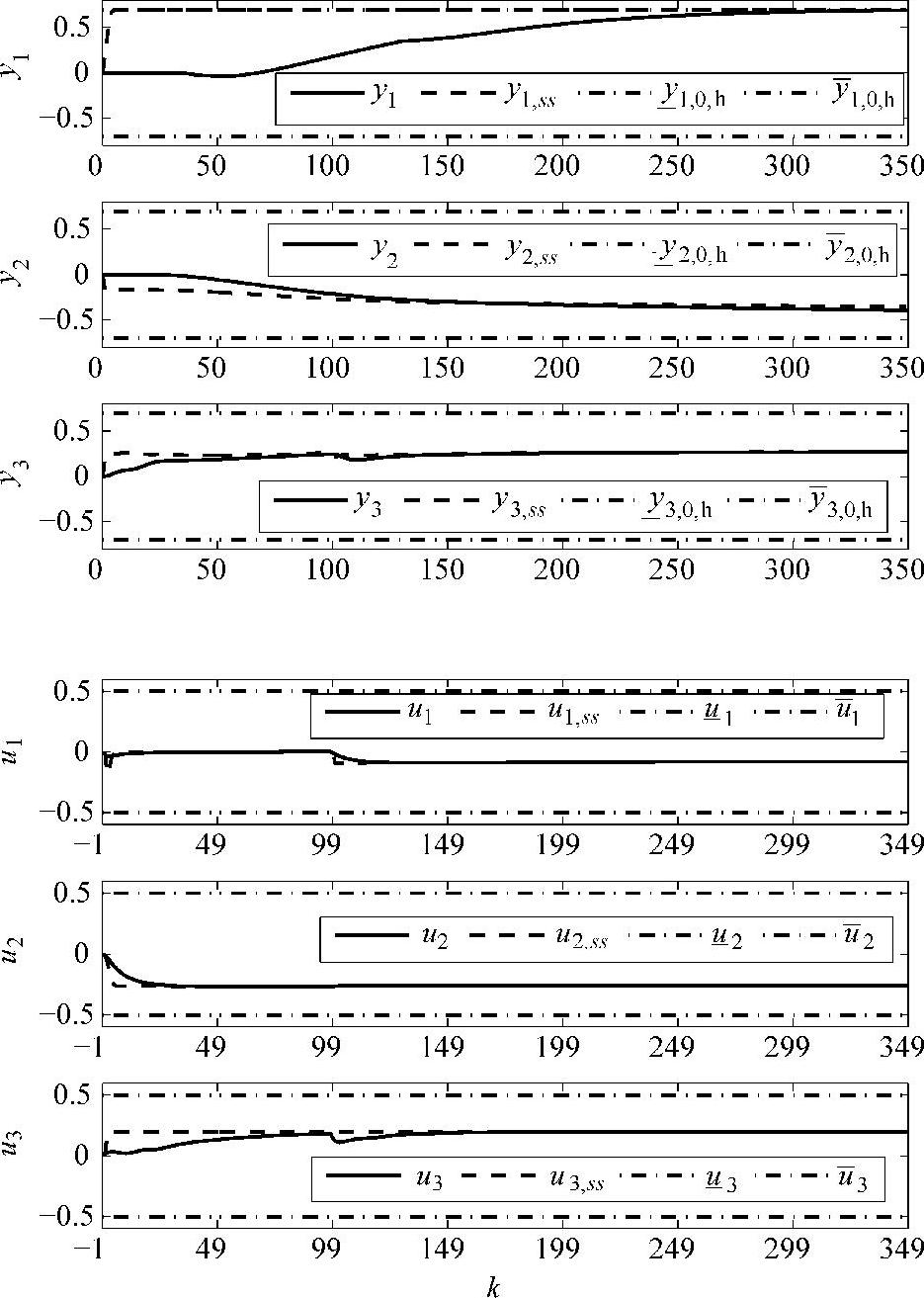
图5-4 第Ⅲ类积分控制效果图
5.第Ⅴ类积分问题,即y2为伪积分。将第4章提供的重油分馏塔的数学模型进行改造,将y2改造为伪积分变量,改造后相应的连续时间传递函数矩阵如下:
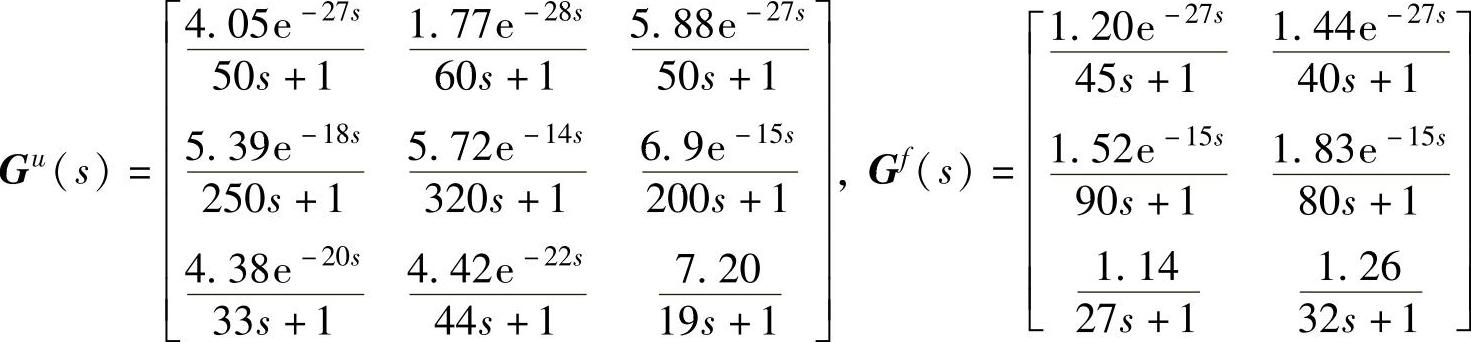
以上模型的阶跃响应曲线如图5-6所示。从图5-6中可以看出y2的稳态响应时间明显大得多(约为其他CV的稳态响应时间的3~4倍)。取采样周期为4,稳态响应时间为400,模型时域N=100。采用MATLAB指令tfd2step,利用以上传递函数矩阵得到式(5-1)所示的FSR模型。取yeq=0、ueq=0和feq=0。
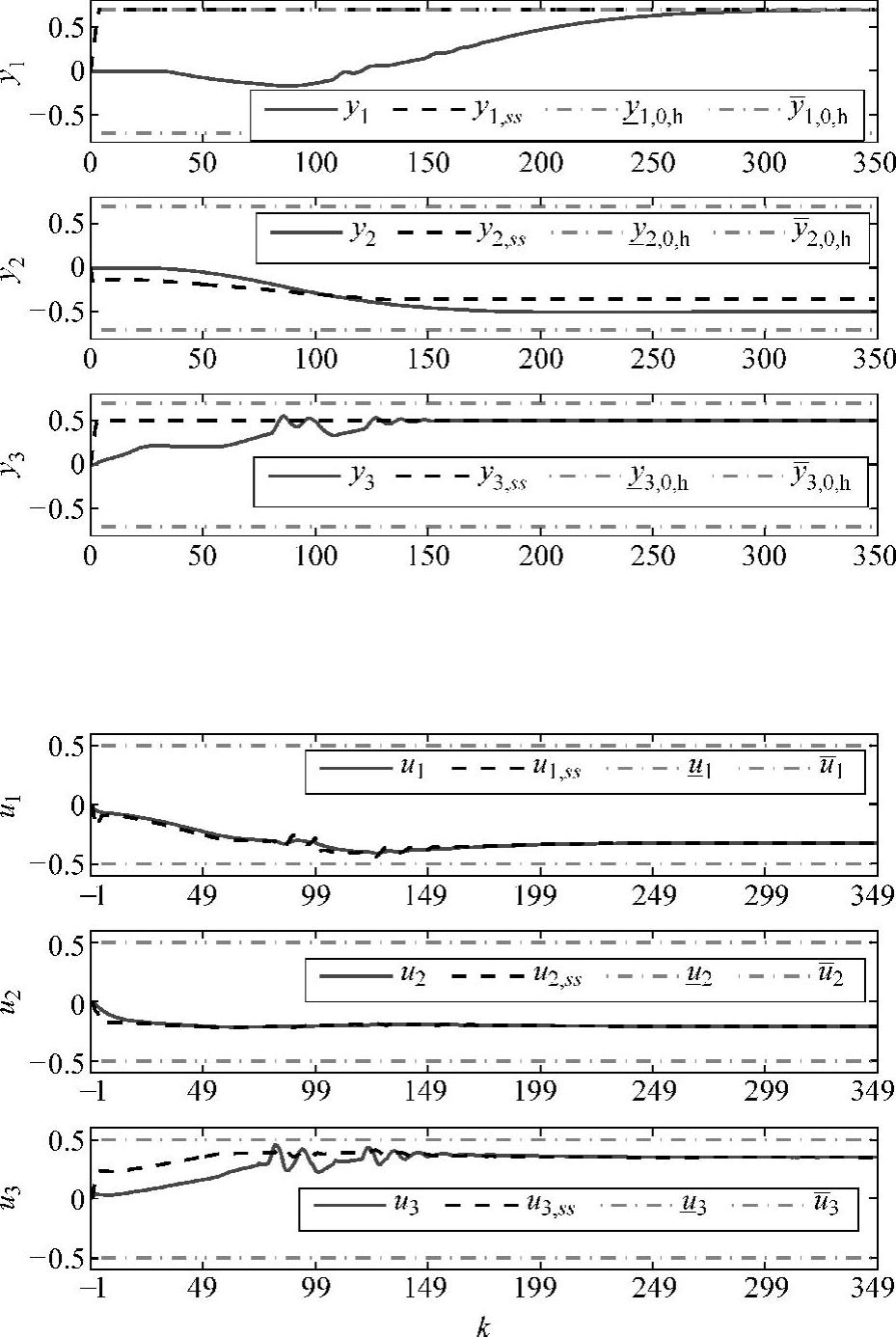
图5-5 第Ⅳ类积分控制效果图
在开环预测部分,积分旋转因子σ2=0.1,采用一阶惯性滤波,平滑系数α=0.5。不同于Ⅰ~Ⅳ类积分,对参数重新设置: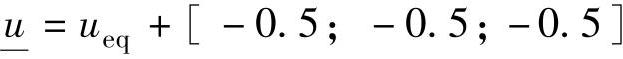 ,
,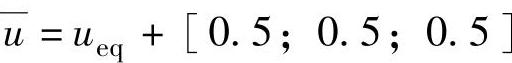 ,
,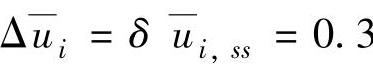 ;
;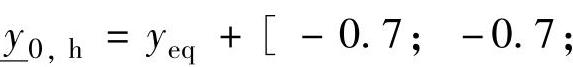 -0.7,
-0.7,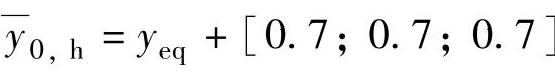 ,
,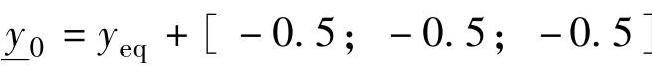 ,
,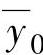 =yeq+[0.5;0.5;0.5],
=yeq+[0.5;0.5;0.5],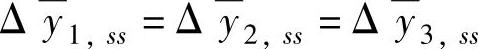 =0.3。y1,ss,y2,ss,u3,ss具有外部目标并且其ETrange均为0.5。在SSTC的经济优化阶段,u2为最小动作变量,取h=[1,2,2]、Jmin=-0.3。在k≥99,有值为feq+[0.20;0.10]的干扰;其他时段内干扰为feq。
=0.3。y1,ss,y2,ss,u3,ss具有外部目标并且其ETrange均为0.5。在SSTC的经济优化阶段,u2为最小动作变量,取h=[1,2,2]、Jmin=-0.3。在k≥99,有值为feq+[0.20;0.10]的干扰;其他时段内干扰为feq。
SSTC可行性和经济优化阶段均采用LP,在获取稳态目标之后,采用动态控制模块来求取MV。选择P=15,M=8,Λ=diag{7,9,7},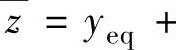
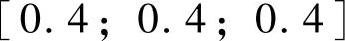 ,
,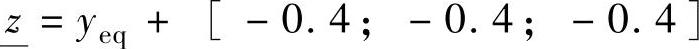 ,
,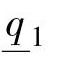 =0.6,
=0.6,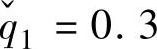 ,
,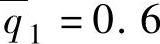 ,
,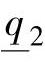 =0.6,
=0.6,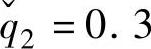 ,
,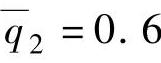 ,
,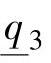 =0.6,
=0.6,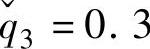 ,
,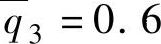 。在进行
。在进行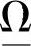 和
和 的确定时,参数ρ=1。u(-1)=ueq,y(0)=yeq,u(k)=u(kk)。真实系统输出用MATLAB和SIMULINK,利用以上传递函数矩阵产生,并乘以0.9来代表模型与实际系统失配。
的确定时,参数ρ=1。u(-1)=ueq,y(0)=yeq,u(k)=u(kk)。真实系统输出用MATLAB和SIMULINK,利用以上传递函数矩阵产生,并乘以0.9来代表模型与实际系统失配。
取Mib=5,外来设定值yr2,sp=y2,eq-0.3,设定值速率κ2=0。控制结果见图5-7,SSTC层给出的CV和MV的稳态值可以被动态控制层完全跟踪上。
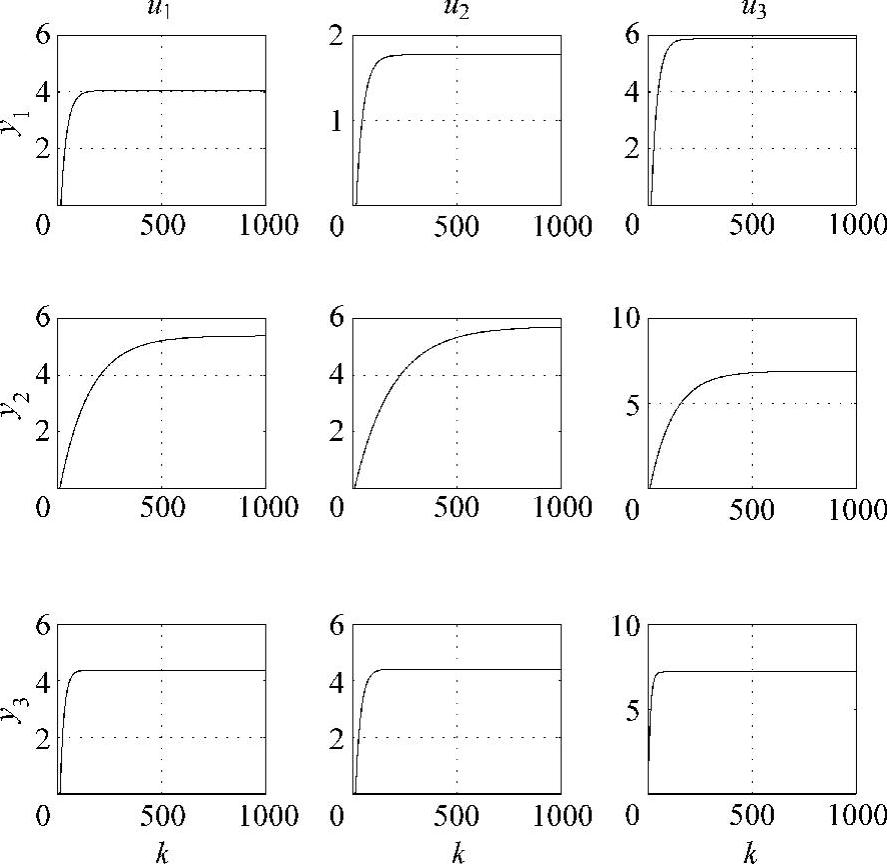
图5-6 含有伪积分模型的阶跃响应曲线图
注意,在本节的算例中,取任意其他合适的{y,u,f}eq时,本章算法仍然可用。此处容易误解为需要满足yseq=Su,sNueq+Sf,sNfeq和yrSlope,eq=Ru,rueq+Rf,rfeq,其中,yrSlope,eq=0为平衡点处的积分稳态斜率,而Rf,r=Sf,rN+1-Sf,rN。
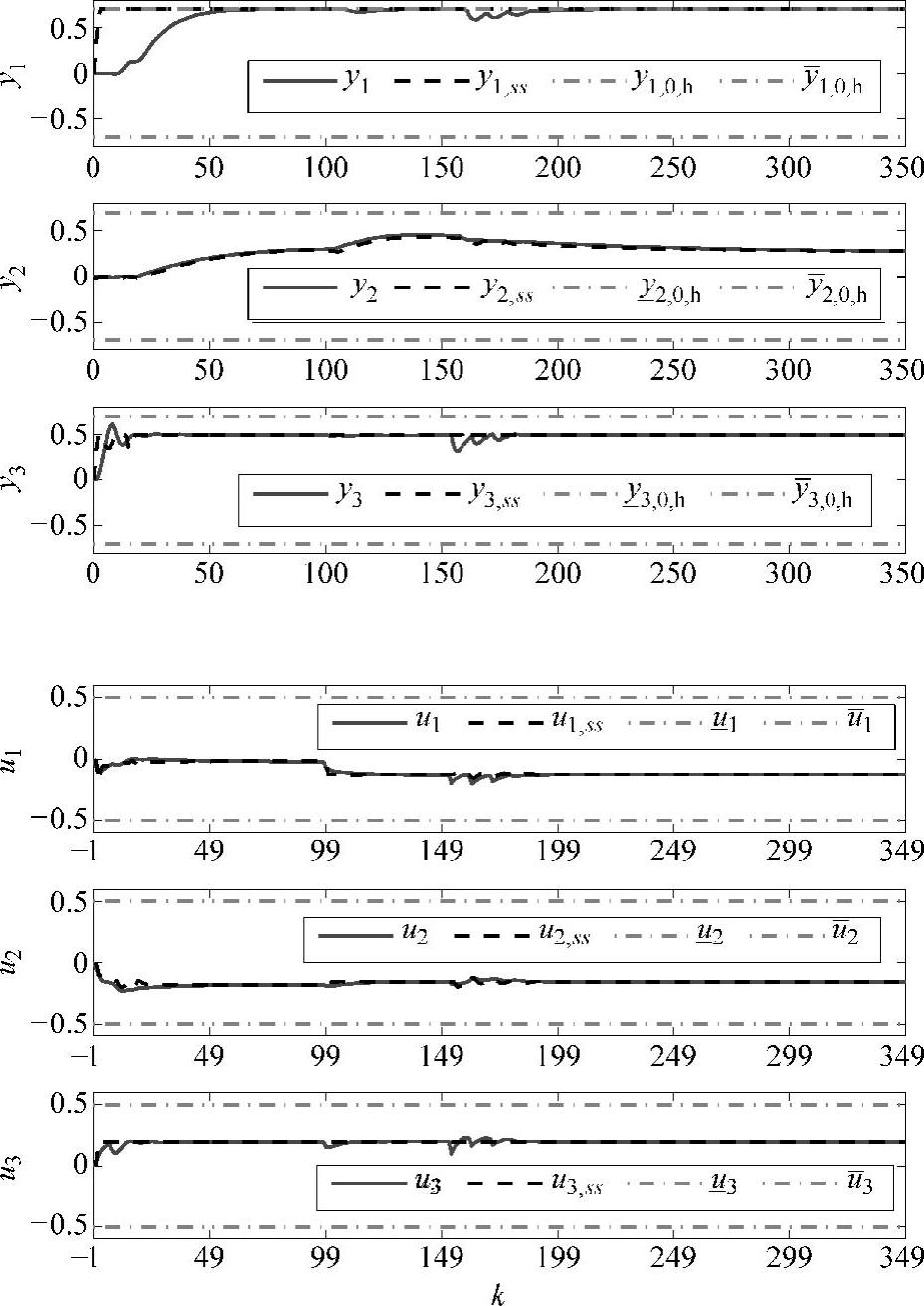
图5-7 第Ⅴ类积分控制效果图
考虑如下传递函数矩阵描述:

将3个CV都当作第Ⅲ类积分处理,则闭环系统能够镇定。进一步,如果模型不变,而对产生真实系统输出的传递函数矩阵做如下修改:
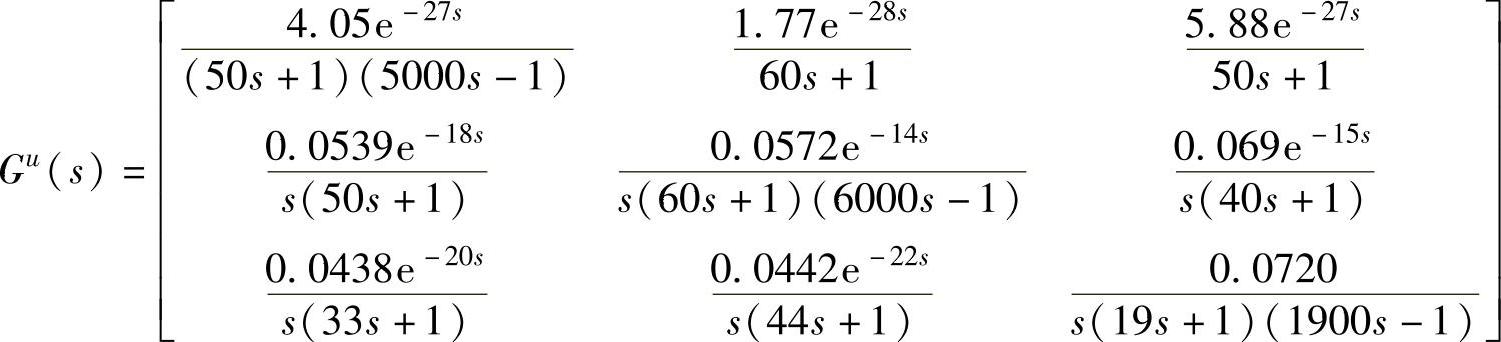
则闭环系统未能镇定。如果产生真实系统输出的传递函数矩阵不变,而阶跃响应模型做如下改变(翘尾):
Sui←(1+0.01e0.01i)Sui,Sfi←(1+0.01e0.01i)Sfi
则闭环系统能够镇定;如果产生真实系统输出的传递函数矩阵不变,而阶跃响应模型做如下改变(拖尾):
Sui←(1-0.001e0.01i)Sui,Sfi←(1-0.001e0.01i)Sfi
则闭环系统能够镇定。以上能镇定的情况需要修改一些参数。针对一系列仿真,总结如下:
系统不可不稳定,模型可以不准确。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




