动态控制算法的优化策略

在动态控制中，假设要达到3个目的：①未来的CV尽量接近规划的设定值轨迹；②抑制MV的剧烈变化；③不可行时，通过放松CV软约束得到可行解。两类CV在动态控制中一并考虑。选择最小化如下的目标函数：

其中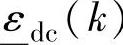，和为输出约束松弛量。目标函数中的加权常取为

对稳定型CV和第Ⅰ类积分型CV，所有以上加权参数的取法同第4章（此处略）。对第Ⅱ～Ⅴ类积分问题，按照如下方式选取加权参数：

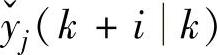的选择与y^ol_j（k+ik）、y^r_j，ss（k+ik）有关系，采用如下标准：

•如果y^ol_j（k+ik）＞max{y^r_j，ss（k+ik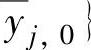），或者y^ol_j（k+ik）＜min{y^r_j，ss（k+ik），，则应该取，以便让CV尽快进入操作约束范围内；

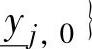•如果y^r_j，ss（k+ik）≥max{y^ol_j（k+ik），，则应该取，以便延缓CV向约束上界靠近；如果y^r_j，ss（k+ik）≤min{y^ol_j（k+ik），，则应该取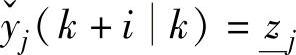，以便延缓CV向约束下界靠近；

•不属于以上两种情况，则取。未说明的符号同第4章。

不同于对y_ss（k）的跟踪，对δu_ss（k）的跟踪通过在动态控制优化问题中加入如下的约束来实现：(www.xing528.com)

其中，L=[II…I]。在动态控制中，通常考虑如下一些不等式约束（MV变化速率约束、MV幅值约束、CV幅值约束、松弛变量约束）：

其中，i为的第i个块行，

此外，第Ⅰ类积分问题需要对MV动态变化路径进行限制，故还要加入如下约束：

其中，L_b=[（M-1）I（M-2）I…0]，见式（5-28）。

总之，在每个时刻k，首先求解优化问题，s.t.式（5-106）～式（5-109），式（5-113）（5-114）

如果式（5-114）不可行，则进一步求解，s.t.式（5-106）～式（5-108），式（5-110）～式（5-113）

优化问题式（5-114）、式（5-115）都可以采用标准的QP求解。在所得的解Δu～（kk）中，仅有Δu（kk）是送入实际被控系统的。按照第4章的方法，可以给出DMC的无约束最小二乘解。第3章求解等式约束QP的Lagrange方法可以用于给出仅含等式约束的DMC的最小二乘解。