仅考虑一阶积分过程。不同类型积分问题的区别,体现为对如下的稳态速率模型、稳态模型与稳态速率约束的重视程度。
1.稳态速率模型
积分型CV的稳态变化速率仅决定于δuss(k)的大小,而与MV动态变化路径无关。在每个时刻k,在假设从k开始MV不再变化的情况下,可预报积分型CV的开环稳态变化速率yr,olSlope,ss(k)[见式(5-13)],该速率已经考虑了干扰和对预测误差的反馈校正)。这样,为了使积分系统稳定,δuss(k)的计算就要抵消yr,olSlope,ss(k)。因此,对积分型CV,考虑如下的速率平衡方程:
其中,Ru,r=Su,rN+i-Su,rN-1+i,∀i≥0为MV影响积分型CV的速率增益矩阵。式(5-23)定义了一个由速率平衡方程规定的操作变量增量δuss(k)的集合。
考虑稳态速率迭代式
其中,yrSlope,ss(k+ik)为在k时刻预测的k+i时刻的稳态速率,假设k+i以后u不再变化。假设动态控制的控制时域为M,且
由式(5-24)~式(5-25)迭代得到
当满足式(5-23)时,由式(5-26)得到yrSlope,ss(k+Mk)=0。
2.速率平衡时的稳态预测模型
速率平衡时,由于式(5-23)严格满足,故实施δuss(k)可达到稳态。在可达到稳态的情况下,同样的δuss(k)在不同的MV动态变化路径下,得到的CV稳态值是不同的(这是积分型CV与稳定型CV的本质不同的地方)。这样需要在动态控制中对MV动态变化路径进行限制。由于模型时域N表示阶跃响应的斜率在N-1个采样周期达到稳态(注意这个假设与第2、4章不同),故yrSlope,ss(k+Mk)=0表示yr(k+M+N-1+ik)=yrss(k),∀i≥0。因此,根据式(5-6)和式(5-14),从k时刻开始连续有M次控制作用变化时的积分CV稳态预测值如下:
其中,Su,rN为积分过程在模型时域点处的增益(称为“点增益”)。
由于δub(k)和δuss(k)的关联关系,表达δub(k)需要满足的约束很复杂;除非将Δu(k+ik)(i=0,1,…,M-1)作为SSTC的决策变量,否则难以准确、方便地优化δub(k)。参考文献[20]给出了δub(k),但是没有给出其对应的具体约束条件。在此,令
其中,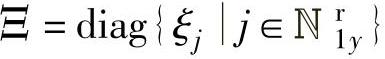 。强制满足式(5-28),形成对MV动态变化路径的限制。故积分CV稳态预测值如下:
。强制满足式(5-28),形成对MV动态变化路径的限制。故积分CV稳态预测值如下:
其中,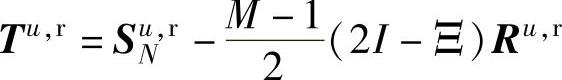 ,最后一个等号用到了式(5-23)。
,最后一个等号用到了式(5-23)。
注解5.3 Ξ为可调参数。当取ξj=1时,在动态控制中可以取M个控制增量相等,这对MV的幅值和速率约束是可行的,但对输出约束未必可行。当去除积分环节后的阶跃响应有反向特性时,应该减小ξj;当去除积分环节后的阶跃响应有超调特性时,应该增大ξj。
3.稳态速率约束
对积分型CV,在其整个取值范围内,进行如下分区:
•安全区(狩猎区):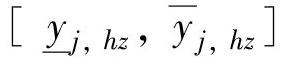 ,下角标“hz”表示“huntingzone”;
,下角标“hz”表示“huntingzone”;
•平衡区(保护区): ,下角标“pz”表示“protectingzone”;
,下角标“pz”表示“protectingzone”;
•危险区(养殖区):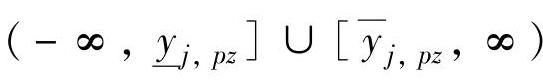 。
。
由前面的推导可知,稳态速率由式(5-26)计算。在实际的SSTC中,计算该稳态速率还需要满足一定的稳态速率约束,该约束代替了相应的稳态目标约束。为了实时地确定稳态速率约束,设置积分型CV安全时域L,满足L≤N,这样稳态速率约束的目的为:如果积分型CV已经进入危险区,则在至多L个控制周期内将其“拉”回到平衡区和安全区范围内;如果积分型CV已经位于平衡区,则阻止其向紧邻的危险区靠近;如果积分型CV位于安全区,则允许其变化但在L个控制周期内达不到平衡区。
定义
其中,κj为积分型CV(第j个CV)设定值速率;yrj,sp为积分型CV(第j个CV)的外部设定值(External Setpoint,ES;或称理想设定值)。计算实时最小、最大容许失衡值
从而引入如下速率约束:(https://www.xing528.com)
式(5-23)相当于式(5-31)当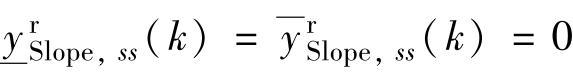 的情况。计算实时最小、最大容许失衡值的起点
的情况。计算实时最小、最大容许失衡值的起点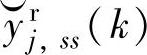 在安全区内与动态控制模块是一致的,设置平衡区和危险区的主要目的是为了消除积分CV失衡、超界对闭环系统稳定性的影响。
在安全区内与动态控制模块是一致的,设置平衡区和危险区的主要目的是为了消除积分CV失衡、超界对闭环系统稳定性的影响。
4.积分问题的区分和设置
考虑如下五类积分:
Ⅰ 如果积分型CV具有经济价值,则需要在SSTC中优化其稳态值,这要求其稳态速率为零。可称为平衡经济型积分CV;
Ⅱ 如果积分型CV与经济目标函数关联不大,但其速率失衡时对生产过程有不利影响,或者容易导致MPC控制器失控,则要求其稳态速率为零。可称为失衡禁止型积分CV;
Ⅲ 如果积分型CV与经济目标函数关联不大,且其暂时速率失衡时对生产过程和MPC控制器影响不大,则允许其稳态速率暂时不为零。可称为期望平衡型积分CV;
Ⅳ 如果积分型CV与经济目标函数关联不大,且其速率失衡对生产过程和MPC控制性能无本质影响,则允许其稳态速率不为零。可称为失衡允许型积分CV;
Ⅴ 如果某一稳定CV对输入的响应较慢,远慢于其他CV对输入的响应,此时从整体角度考虑可选择较小的模型时域。这样,响应快的CV达到稳态时,响应慢的CV还处于上升或下降阶段,这些响应慢的CV看起来就像积分CV,故称为伪积分CV。
其中,Ⅰ~Ⅳ是真正的积分CV,而V不是。这里关于第Ⅱ~Ⅴ类积分的思想来源于对Aspen Technology的工业MPC软件的学习,特此说明。
注解5.4 参考文献[85](第74页)中,相当于建议:对“有一时间常数较大的主特征运动”的伪积分,将本书的yr,ol(k+N+1k-1)-yr,ol(k+Nk-1)=yr,ol(k+Nk-1)-yr,ol(k+N-1k-1)替换为yr,ol(k+N+1k-1)-yr,ol(k+Nk-1)=σ[yr,ol(k+Nk-1)-yr,ol(k+N-1k-1)],其中可取σ∈(0.9,1),即将模型参数截断后的指数变化信息用σ反映出来。读者可构思其相应的SSTC问题的解决方法。本书中相当于取σ=1,是一种与其他类型积分相对一致的处理方式。
在五类积分问题中,对式(5-19)~式(5-21)、式(5-23)和式(5-31)有不同的处理方式,具体地
(1)对第Ⅰ类积分,加入式(5-23)作为硬约束,并加入约束式(5-19)~式(5-21)。不考虑式(5-31);
(2)对第Ⅱ类积分,加入式(5-23)作为硬约束。不考虑式(5-19)~式(5-21)和式(5-31);
(3)对第Ⅲ类积分,加入式(5-23)作为软约束,并加入式(5-31)作为硬约束。如果连续速率失衡次数超过连续失衡最大容许次数Mib,则需停止运行MPC。不考虑式(5-19)~式(5-21);
(4)对第Ⅳ类积分,加入式(5-31)作为硬约束。不考虑式(5-19)~式(5-21)和式(5-23);
(5)对第Ⅴ类积分,加入式(5-23)作为软约束。如果连续速率失衡次数超过连续失衡最大容许次数Mib,则需停止运行MPC。不考虑式(5-19)~式(5-21)和式(5-31)。
第Ⅰ、Ⅱ类积分问题要求速率平衡[即满足式(5-23)],而其他类积分问题允许速率失衡[即不满足式(5-23)];前四类积分问题要求稳态速率满足某种硬约束,而第Ⅴ类不加速率硬约束;除第Ⅰ类积分问题外,其他类积分都不考虑式(5-19)~式(5-21)。此外,
(1)对第Ⅰ类积分问题,相当于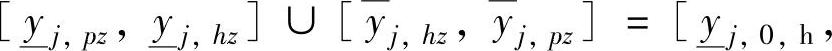
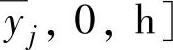 ,只有平衡区(没有安全区和危险区),满足
,只有平衡区(没有安全区和危险区),满足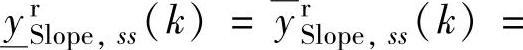
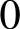 或L→∞。
或L→∞。
(2)对第Ⅱ类积分问题,相当于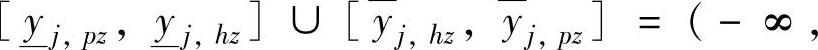
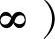 ,只有平衡区(没有安全区和危险区),满足
,只有平衡区(没有安全区和危险区),满足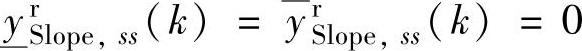 或L→∞。由于并不考虑式(5-19)~式(5-21),因此条件比第Ⅰ类积分问题更宽松。
或L→∞。由于并不考虑式(5-19)~式(5-21),因此条件比第Ⅰ类积分问题更宽松。
(3)对第Ⅲ类积分问题,有三个区,可能出现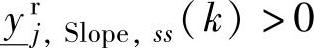 或者—yrj,Slope,ss(k)<0的情况,故第Ⅲ类积分的条件未必比第Ⅰ、Ⅱ类积分更宽松。
或者—yrj,Slope,ss(k)<0的情况,故第Ⅲ类积分的条件未必比第Ⅰ、Ⅱ类积分更宽松。
(4)对第Ⅳ类积分问题,同第Ⅲ类。由于不设置Mib,第Ⅳ类积分的条件比第Ⅲ类积分更宽松。
(5)对第Ⅴ类积分问题,相当于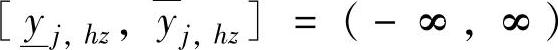 ,只有安全区(没有平衡区和危险区)。第Ⅴ类积分的条件比第Ⅰ、Ⅱ、Ⅲ类积分更宽松。
,只有安全区(没有平衡区和危险区)。第Ⅴ类积分的条件比第Ⅰ、Ⅱ、Ⅲ类积分更宽松。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




