CV中的积分型部分如何优化？

仅考虑一阶积分过程。同稳定型CV，对积分型CV要对未来N步做出预测。在k＞0时刻，检测到Δu（k-1）的实际值后，根据式（5-5）可计算出

y^r，ol（kk）=y^r，ol（kk-1）+S^u，r₁Δu（k-1）

其中，上角标“fr”改为“ol”。基于实测输出y^r（k）得

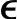^r（k）=y^r（k）-y^r，ol（kk）=y^r（k）-y^r，ol（kk-1）-S^u，r₁Δu（k-1）

该^r（k）反映了阶跃响应模型中未包含的不确定因素对积分型输出的影响，称为预测误差。对^r（k）进行滤波处理，以一阶惯性滤波为例得到

′^r（k）=α^r（k）+（1-α）′^r（k-1），k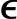＞0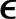，′^r（0）=^r（0）

采用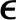′^r（k）进行反馈校正，取为

e^r（k+ik）=（I+i∑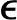）′^r（k），i≥0 （5-11）

其中，∑=diag{σ_jj∈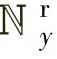}，σ_j∈[0，1]为积分旋转因子（rotationfactor）（读者可考虑一阶惯性滤波和旋转因子如何利用Kalman滤波解释）。即假设′^r（k）的影响分为两部分：恒值和积分，这对积分型输出变量通常是合适的。综合式（5-5）和该反馈校正得到

式（5-12）称为开环动态预测方程。

注解5.1 如果某个被控制系统具有对能量或物质进行累加或累减的能力，那么这种能力将表现在CV上，该CV对于所有与之有关联的独立变量呈现出来的动态特性全部具有积分特性。对于过程的可测DV，可以辨识其与CV之间的动态数学模型进而在开环预测中明确地考虑，但对于不可测DV，只能通过反馈校正进行补偿。但是，恒值的反馈校正无法体现不可测DV对一阶积分过程的影响，所以针对积分CV，在实施DMC算法时，反馈校正过程应体现积分特点。由于不可测DV对CV的影响的稳态斜率未知，所以只能通过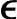′^r（k）启发式地进行计算。比如，如果我们相信′^r（k）都是由于稳态斜率的不准确性造成的，则该一步预报误差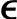′^r（k）用于多步反馈校正时，其校正值就要乘以预测步长。一般来说，可以认为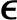′^r（k）中的一部分是由稳态斜率的不准确性造成的，而另一部分是由非积分型误差造成的。(www.xing528.com)

积分变量旋转因子表征了′^r（k）中将进行积分的部分。如果σ=0，则认为稳态斜率是准确的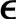，′^r（k）全部为非积分型误差。如果σ=1，则认为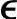′^r（k）全部是由稳态斜率的不准确性造成的。由于使用一个近似的σ对应所有的未知情况，所以如何确定σ是一个比较困难的工作。可以这样在线观察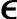′^r（k）对σ进行整定：如果σ取值过小，则′^r（k）将在0的一侧持续很久，而后转移到0的另一侧；如果σ取值过大，则′^r（k）在0值附近上下波动剧烈；如果σ取值合适，则′^r（k）将表现出随机变量的特性。

记从k时刻开始MV不再变化的情况下，积分型CV的稳态变化速率为y^r，ol_Slope，ss（k）。这里的变化速率定义为两个控制周期的差值。则由于采用了式（5-11），

y^r，ol_Slope，ss（k）=y^r，ol（k+ik）-y^r，ol（k+i-1k），i≥N （5-13）

因此，除了由式（5-12）给出的未来N步内的输出预测值外，未来的N+1步外的输出预测值为

注意推导式（5-12）时隐含地用到了关系式y^r，ol（k+Nk-1）-y^r，ol（k+N-1k-1）=y^r，ol（k+N-1k-1）-y^r，ol（k+N-2k-1），这与式（5-13）中k替换为k-1的情形一致，也就是说以上开环稳态和动态预测没有矛盾（具有一致性）。采用式（5-11）满足了这种一致性的需求。

对一般工程问题，要选择N比实际的稳态响应时间（为稳定型CV和积分型CV中稳态响应时间的最大值）大一个控制周期，且根据以上的推导可知：稳定过程的开环动、稳态预测公式（5-9）～式（5-10）是一阶积分过程的开环动、稳态预测公式（5-12）～式（5-13）当旋转因子为0时的特殊情况。

注解5.2 所用到的符号见第4.4节。记k时刻的开环动态预测值如下：

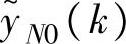是Y^ol_N（kk）中元素重排的结果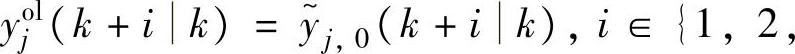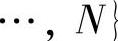，。将式（5-9）与式（5-12）合并，并给出等价的结果为

其中