稳定型CV部分优化方法

在k＞0时刻，检测到Δu（k-1）的实际值后，根据式（5-2）可计算出

其中，上角标“fr”改为“ol”。基于实测输出y^s（k）得

该^s（k）反映了阶跃响应模型中未包含的不确定因素对稳定型输出的影响，称为预测误差。由于^s（k）可能包含了噪声的影响，可对其进行滤波处理，以一阶惯性滤波为例得到

′^s（k）=α^s（k）+（1-α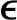）′^s（k-1），k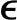＞0，′^s（0）=^s（0）

其中，α∈（0，1]为平滑系数。采用′s（k）对未来输出的开环动态预测值进行校正，称为反馈校正。假设反馈校正在未来所有时间点都是恒定的，即

e^s（k+ik）=′^s（k），i≥0 （5-8）(https://www.xing528.com)

这相当于假设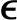′^s（k）为输出端阶跃型干扰，对稳定型输出变量通常是合适的。综合式（5-2）和该反馈校正得到

其中，。式（5-9）称为开环动态预测方程。注意在式（5-2）中没有考虑反馈校正，而在式（5-9）中则考虑了反馈校正。

由于采用了式（5-8），故开环稳态预测为

y^s，ol_ss（k）=y^s，ol（k+N-1+ik），∀i≥0. （5-10）

注意推导式（5-9）时隐含地用到了关系式y^s，ol（k+Nk-1）=y^s，ol（k+N-1∣k-1）=y^s，ol（k+N-2k-1），这与式（5-10）中k替换为k-1的情形一致，也就是说以上开环稳态和动态预测没有矛盾（具有一致性）。采用式（5-8）满足了这种一致性的需求。