被控系统的数学模型探讨

考虑如下的有限阶跃响应模型（对所有N′≥N-1等价）：

其中，S^u，s_i、S^f，s_i分别为针对u、f的阶跃响应系数矩阵，满足S^u，s_N-1+i=S^u，s_N-1和S^f，s_N-1+i=S^f，s_N-1，∀i≥0（注意：与第2、4章不同）。采用式（5-1）进行预测得到

对于积分型输出，应该采用输出、脉冲响应系数、阶跃响应系数的增量，即式（5-1）应该替换为（对所有N′≥N等价）

其中，S^u，r_i、S^f，r_i分别为针对u、f的阶跃响应系数矩阵，满足S^u，s_N+i-S^u，s_N-1+i=S^u，s_N-S^u，r_N-1和S^f，r_N+i-S^f，r_N-1+i=S^f，r_N-S^f，r_N-1，∀i≥0（注意，与第2章不同）。在式（5-4）两边不能去掉Δ，因为积分型输出不能表示为MV、DV的有限项的加权和。采用式（5-4）进行预测得到(www.xing528.com)

显然，式（5-5）～式（5-6）和式（5-2）～式（5-3）具有统一的形式。

在式（5-1）和式（5-4）中，采用了相对于平衡点的变化量（由算子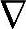表示。在实际工业应用中，{y，u，f}_eq是由实际工况自然形成的，不需要满足任何预设的映射关系），但是在此后的推导中，一律采用实际实施值或者测量值，而非相对于平衡点的变化量。基于式（5-2）～式（5-3）或者式（5-5）～式（5-6），并考虑反馈校正，做开环和闭环预测。原理同第2章的Kalman滤波方法。考虑反馈校正后，从k时刻开始MV不再变化的情况下，得到的预测值y^ol（k+ik）称为开环预测，其中，上角标“ol”表示开环（open-loop）。记k时刻的开环动态预测值如下：

一般取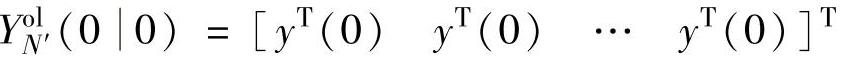作为初值。