无约束动态矩阵控制的实现方法

假设过程模型包含n_u个MV和n_y个CV，已知每个y_i对u_j的阶跃响应s_ij（l），则可由它们在采样点上的值组成模型向量

假设模型开环稳定，没有积分型CV。以下的阐述按照所谓的预测控制“三大原理”展开，即预测模型、滚动优化、反馈校正。在无约束控制中，它们分别对应双层DMC中的闭环预测方程、最小二乘解、开环预测模块。

1.预测模型

考虑在u_j作用下对y_i的预测。首先写出只有一个增量Δu_j（kk）时，在未来N个时刻的y_i的预测值为

其中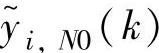，表示在k时刻全部控制量u₁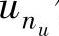，…，保持不变时，对y_i在未来N个时刻的初始预测值（即开环预测值）；

类似地，在u_j依次有M个增量变化Δu_j（kk），…，Δu_j（k+M-1k）时，可得未来P个时刻的y_i的预测值；

其中，

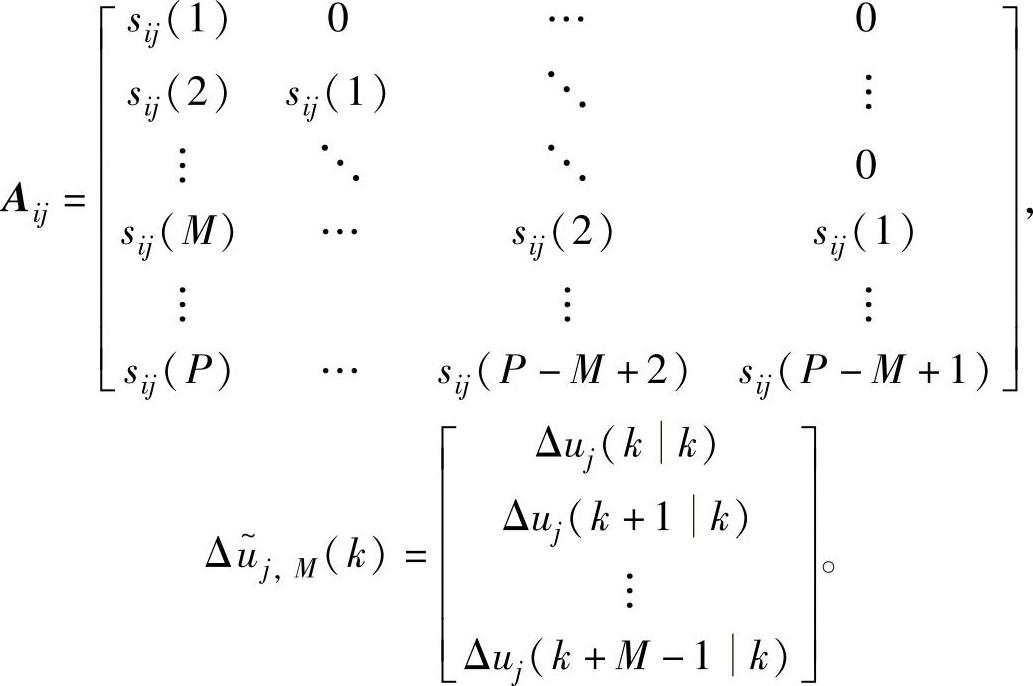
式（4-102）～式（4-103）就是y_i在u_j单独作用下的预测模型。若y_i受到u₁（k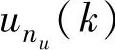），…，的共同作用，则可利用叠加原理。若各u_j只有即时变化Δu_j（kk），则对应于式（4-102），有

若各u_j从k时刻起均变化M次，即有控制增量Δu_j（kk），…，Δu_j（k+M-1k）（j=1，…，n_u），对应于式（4-103），有

定义合成向量和矩阵

则可得到一般的多变量系统的一步和多步预测模型，即

显然，式（4-82）为式（4-105）的重组形式。

2.滚动优化

在每一个控制周期最小化

其中，

Q和R分别为非负的误差权矩阵和控制权矩阵。将式（4-105）代入式（4-106），通过极值必要条件，当（A^TQA+R）-1可逆时，得到最优控制增量

即时控制增量可以通过下式给出(www.xing528.com)

其中

而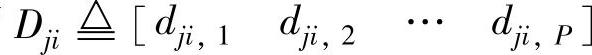，L=diag{[1 0 … 0]，…，[1 0 … 0]}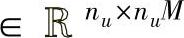。等价地，

3.反馈校正

在k时刻，假定控制作用保持不变时，对未来时刻有初始预测值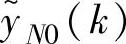。当k时刻实际实施Δu（k）后，则可预测未来时刻的CV值

其中，

与式（4-104）不同，式（4-111）采用的是Δu（k）而不是Δu（kk）。由于执行机构的反应速度等原因，可能Δu（k）≠Δu（kk）。取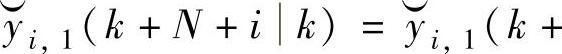。向量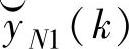是构造k+1时刻的开环预测值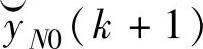的基础。

在的计算中，没有用到实测数据y（k+1）。由于实际存在的模型失配、不可测（未建模）干扰、噪声等不确定因素，可能出现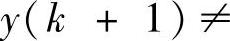。假设不存在测量噪声，则应采用误差向量

对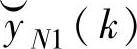进行校正。（k+1）反映了模型中未包括的不确定因素对一步CV预测的影响。我们希望用（k+1）产生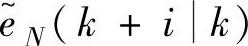，并按照如下公式校正：

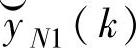其中，

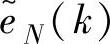由于缺乏对的因果性描述，故只能采用经验方法产生，常见为

称H为误差校正矩阵。如果取h_ii（1）=1且所有其他h_ij（1）=0，则能够保证，实现了对的准确校正。由于缺乏各CV预测误差对各CV预测值的交叉影响的先验知识，交叉校正向量H_ij（i≠j）的选取是无规则可循的。为简化计算，通常只保留H中的主对角块，即只用y_i自身的预测误差修正其CV预测值。校正系数的选取方法很多，可参考文献[85]；常见的方法是h_ii（l）（l∈{1，…，N}）的取值全为1，就像本章4.1节所述的那样。

在k+1时刻，由于时间基点移动，预测的未来时间点转移到k+2，…，k+1+N，因此，的元素还需要移位才能作为k+1时刻的初始预测值。对进行移位运算，得到

其中，

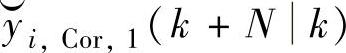由代替。

注解4.12 即使对本节的无约束DMC，稳定性分析也是非常复杂的，早期通常采用内模控制（Inner Model Control，IMC）方法，得到一些特殊结果。理论上，控制器的主要参数（采样周期T_s、模型长度N、优化时域P、控制时域M、误差权矩阵Q、控制权矩阵R、校正参数H）对稳定性都有影响，但若令预测时域P=M+N，且没有模型失配和未建模干扰，则闭环控制系统差不多肯定是稳定的。P=M+N时，得到的即时控制作用相当于无穷时域最优控制作用，故这种参数选择方法间接地利用了无穷时域最优控制的稳定特征。