取预测时域为P,控制时域为M。{M,N,P}之间满足M≤P≤N+M即可,而不同于很多文献中要求M≤P≤N。
在每个时刻k,已知YolN(kk),可以获得
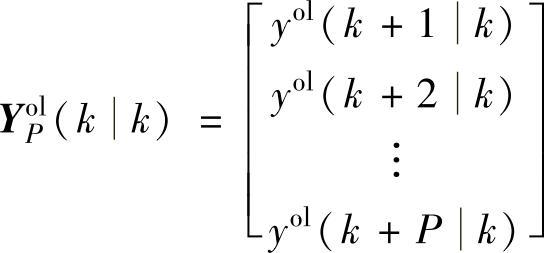
当P>N时,yol(k+jk)=yol(k+Nk),j>N。该预测值已经包含了干扰的影响和预测误差的反馈校正。根据式(4-3),容易得到
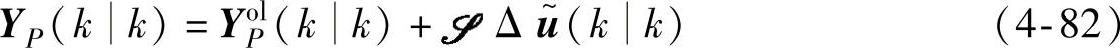
其中

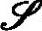 被称为动态矩阵。式(4-82)为闭环预测方程。在预测控制实际运行中,每一时刻可发布MV多步作用下的CV预测信息,该信息反映了对扰动的抑制状况和对设定值跟踪的状况。
被称为动态矩阵。式(4-82)为闭环预测方程。在预测控制实际运行中,每一时刻可发布MV多步作用下的CV预测信息,该信息反映了对扰动的抑制状况和对设定值跟踪的状况。
在动态控制中,假设要达到3个目的:①未来的CV尽量接近yss(k);②抑制MV的剧烈变化;③不可行时,通过放松CV软约束得到可行解。选择最小化如下的目标函数:
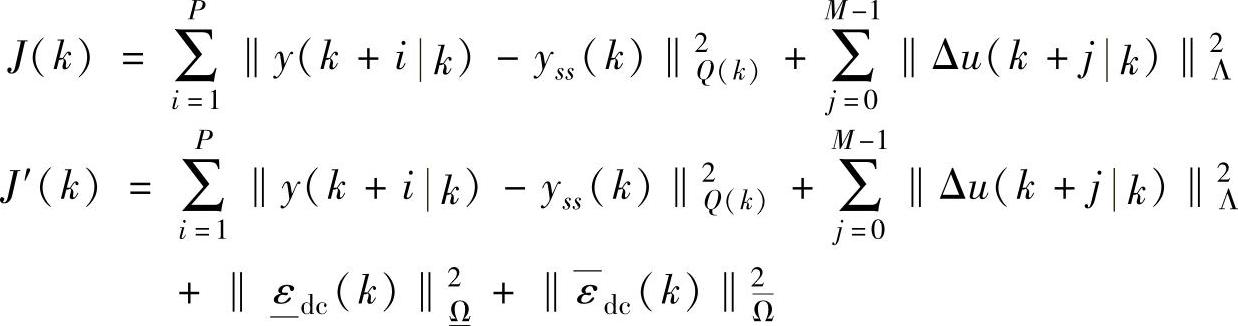
其中,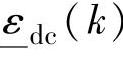 和
和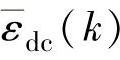 为CV约束松弛量。目标函数中的加权{Q(k),Λ,
为CV约束松弛量。目标函数中的加权{Q(k),Λ,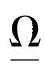 ,Ω}常取为
,Ω}常取为

其中
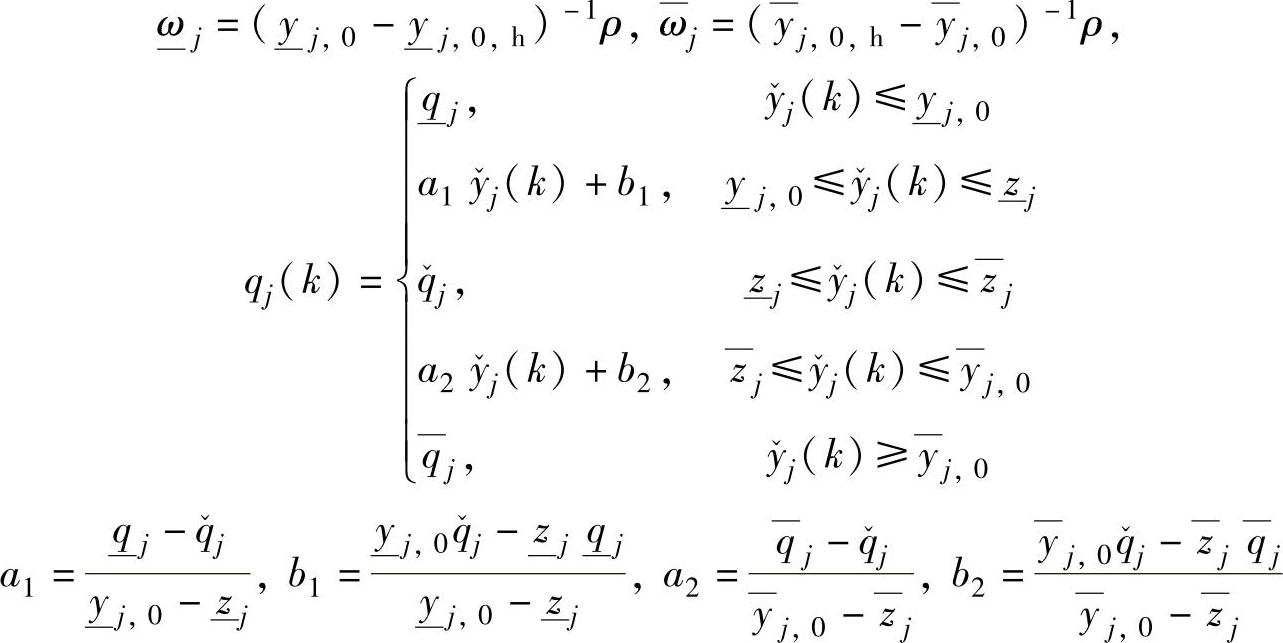
 的选择与y(k)、yolj(k+ik)(i∈{1,2,…,P})、yss(k)都有关系。比如,可以取y(k)与yolj(k+ik)(i∈{1,2,…,P})的算术平均值为yave(k),并采用如下标准:
的选择与y(k)、yolj(k+ik)(i∈{1,2,…,P})、yss(k)都有关系。比如,可以取y(k)与yolj(k+ik)(i∈{1,2,…,P})的算术平均值为yave(k),并采用如下标准:
•如果 或者
或者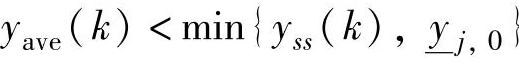 ,则应该取
,则应该取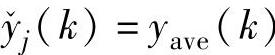 ,以便尽快让CV离开约束界;
,以便尽快让CV离开约束界;
•如果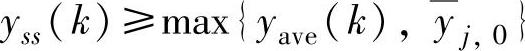 ,则应该取
,则应该取 ,以便延缓CV向约束上界靠近;如果
,以便延缓CV向约束上界靠近;如果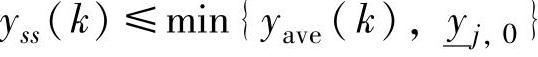 ,则应该取
,则应该取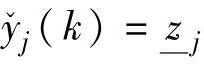 ,以便延缓CV向约束下界靠近;
,以便延缓CV向约束下界靠近;
•不属于以上两种情况,则取 。
。
ρ(调整系数)、{λ1,λ2,…,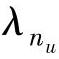 }和
}和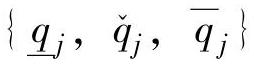 为控制器可调参数(通常
为控制器可调参数(通常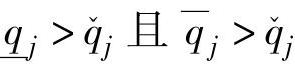 ),
),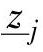 和
和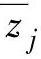 为转换区域的边界。当
为转换区域的边界。当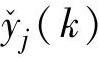 高于CV上界、低于CV下界或者在上下界之间时,采用不同的加权以体现对约束的重视,另外,设置加权的转换区域以防止在
高于CV上界、低于CV下界或者在上下界之间时,采用不同的加权以体现对约束的重视,另外,设置加权的转换区域以防止在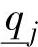 和
和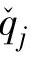 之间或者
之间或者 和
和 来回切换形成振荡。
来回切换形成振荡。
不同于对yss(k)的跟踪,对δuss(k)的跟踪通过在动态控制优化问题中加入如下的约束来实现:

其中,L=[II…I]。在动态控制中,通常考虑如下一些不等式约束(MV变化速率约束、MV幅值约束、CV幅值约束、松弛变量约束):

其中,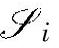 为
为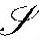 的第i个块行,
的第i个块行,
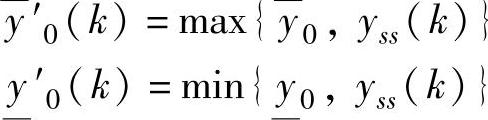
即若CV设定值高于上限,则用设定值作为上限;若CV设定值低于下限,则用设定值作为下限。
总之,在每个时刻k,首先求解优化问题

如果式(4-90)不可行,则进一步求解
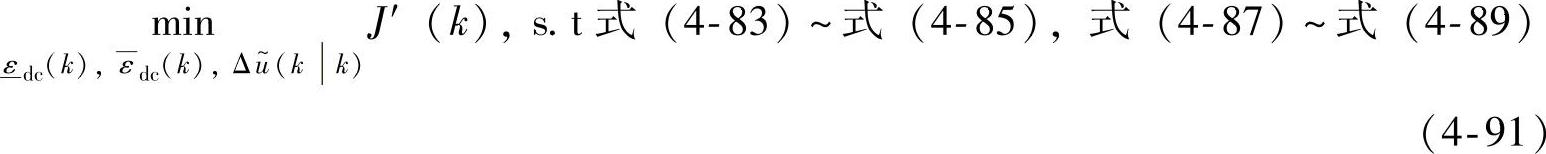
优化问题式(4-90)、式(4-91)都可以采用标准的QP工具求解。在所得的解 中,仅有Δu(kk)是送入实际被控系统的。
中,仅有Δu(kk)是送入实际被控系统的。
求解QP最为常见的方法是内点法和有效集法,而大部分有效的内点法通常称为原始-对偶(primal-dual)算法。这类算法的计算量较大。所以,对于问题规模较大的多变量控制问题,通常没有足够的时间去求解QP问题。由于这个原因,有些商品化的MPC软件采用了一些次优的方法来产生近似的QP解。最为简单的当属PFC(法国Adersa公司的MPC产品),直接采用最小二乘法求解该优化问题,对于超出MV约束界的解直接使用界替代。DMCplus使用了一种稍许复杂的序列最小二乘方法,当计算的某个MV超过其上限或下限时,则令该MV等于该界限值,重新计算最小二乘解。参考文献[37]给出了更合理和复杂的方法,其具体实现可参考文献[85](第110页),比完整的内点法和有效集法计算量低。
注解4.6 在很多文献中,习惯于写Δu(k)=Δu(kk)和u(k)=u(kk)。但注意在实际应用中,由于各种原因,有可能Δu(k)≠Δu(kk)和u(k)≠u(kk)。在实际应用中,在每个时刻k计算MV前,采用u(k-1)的实测值并计算Δu(k-1)=u(k-1)-u(k-2)。
注解4.7 在线控制中,由于Δu(k)还没有被计算出来,总认为每个时刻k检测到的u为k-1时刻发生的。在离线模型辨识中的不同在于,总认为每个时刻k检测到的u为k时刻发生的,这是因为离线辨识时不需要在线优化Δu(k)的缘故。理论公式上的表达,实际上都是基于“瞬时假设”的,也就是隐含地假设了MV优化计算时间、通信时间、执行机构动作时延都可以忽略。
注解4.8 可以不采用式(4-83),代之以在J(k)中加入
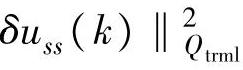 ,其中,Qtrml>0为加权矩阵。定义Yss,P(k)=[yss(k);yss(k);…;yss(k)],
,其中,Qtrml>0为加权矩阵。定义Yss,P(k)=[yss(k);yss(k);…;yss(k)],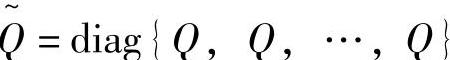 和
和 ,则
,则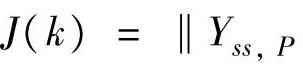
 。最小化
。最小化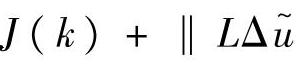
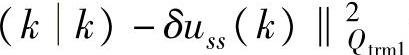 等价于求如下方程组的最小二乘解:
等价于求如下方程组的最小二乘解:
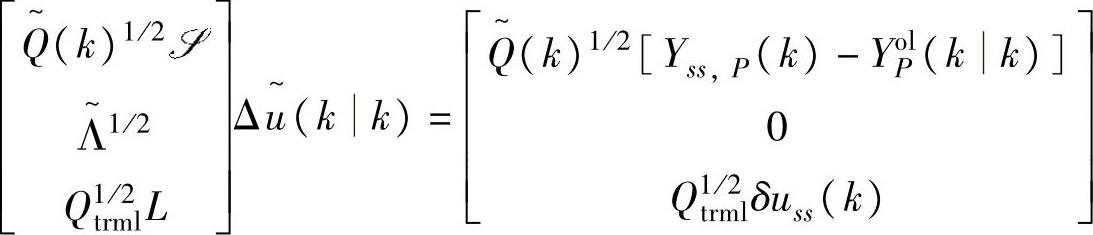
当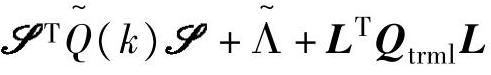 可逆时,解为
可逆时,解为
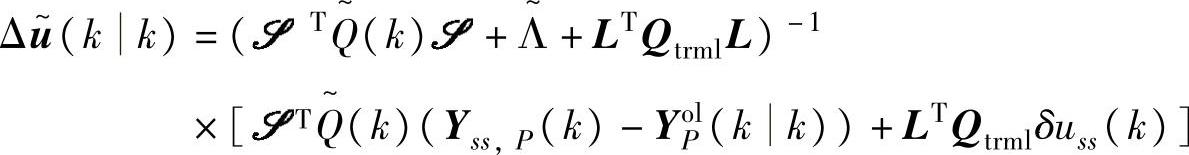
实际求解逆矩阵时一般采用SVD分解。
注解4.9 从减少优化自由度的角度看,在动态控制中加入硬约束式(4-83)相当于让控制时域减小1,因为根据式(4-83)得到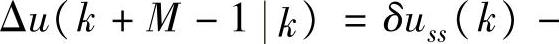
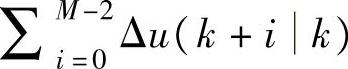 。类似注解4.8,可以得到在满足式(4-83)的情况下,最小化J(k)的
。类似注解4.8,可以得到在满足式(4-83)的情况下,最小化J(k)的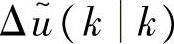 的最小二乘解。
的最小二乘解。
注解4.10 先于式(4-91),求解优化问题(4-90)主要是从控制系统安全性的角度考虑的,即让CV尽量不违反约束式(4-86)。适当地加大 和Ω,可以不用求解式(4-90)。实际上,为了降低计算量,加快动态控制的响应速度,在不影响安全的情况下也可以不求解式(4-90)。另外,一种可行的方法是选定一个参数P″∈{1,2,…,P-1},对i∈{1,…,P″}只要求满足CV的工程约束条件,而仅对i∈{P″+1,…,P}要求满足式(4-86),这时甚至根本不需要引入松弛量
和Ω,可以不用求解式(4-90)。实际上,为了降低计算量,加快动态控制的响应速度,在不影响安全的情况下也可以不求解式(4-90)。另外,一种可行的方法是选定一个参数P″∈{1,2,…,P-1},对i∈{1,…,P″}只要求满足CV的工程约束条件,而仅对i∈{P″+1,…,P}要求满足式(4-86),这时甚至根本不需要引入松弛量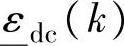 和
和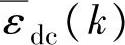 。
。
例4.1 采用第3章提供的重油分馏塔模型,在平衡点附近,其连续时间传递函数矩阵如下:
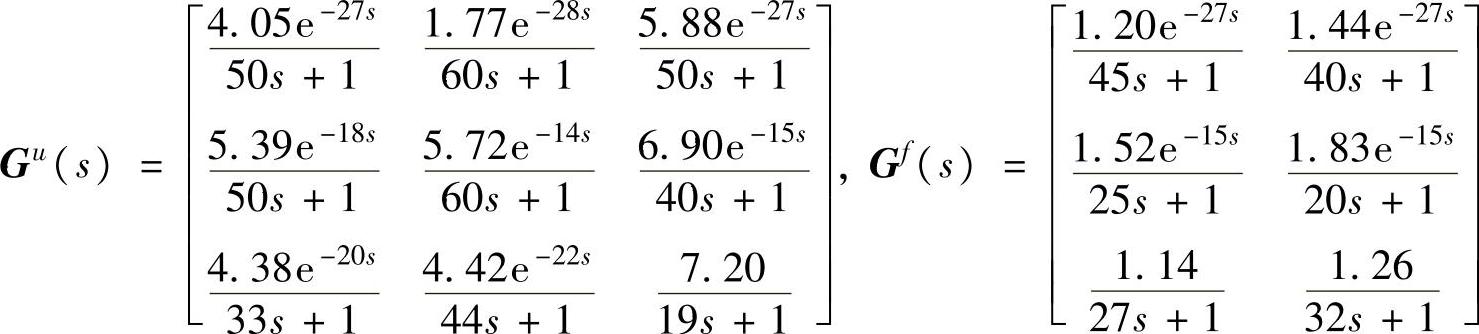
采样周期为4。
取模型时域N=100,采用MATLAB指令tfd2step,用以上传递函数矩阵得到式(4-1)所示的有限阶跃响应模型(即得到分别为针对操作变量u和干扰f的阶跃响应系数矩阵Sui和Sfi)。 、
、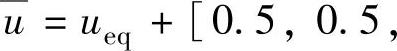
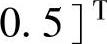 、
、 ;
;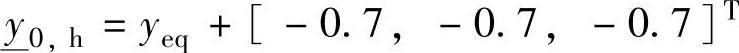 、
、
 、
、 、
、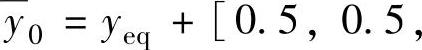
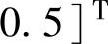 、
、 、
、 、
、 。y1,ss,y2,ss,u3,ss具有外部目标并且其ETrange均为0.5。采用一阶惯性滤波,平滑系数αj=0.5。可行性阶段的相关参数设置见表4-1,在每个优先级中或者只有等式型软约束,或者只有不等式型软约束,含最低优先级软约束。经济优化中,u2为最小动作变量,取h=[-2,1,2]、Jmin=-0.2。在k∈[64,78]时,出现值为feq+[0.20;0.10]的干扰;k≥122时,出现值为feq+[1;-1]的干扰。其他时段内干扰为feq。YolN(00)=[yeq;…;yeq]。取yeq=0、ueq=0和feq=0。下面采用线性规划,给出SSTC的所有优化问题,其中为书写简便,没有完全采用规则r1~r12进行简化。
。y1,ss,y2,ss,u3,ss具有外部目标并且其ETrange均为0.5。采用一阶惯性滤波,平滑系数αj=0.5。可行性阶段的相关参数设置见表4-1,在每个优先级中或者只有等式型软约束,或者只有不等式型软约束,含最低优先级软约束。经济优化中,u2为最小动作变量,取h=[-2,1,2]、Jmin=-0.2。在k∈[64,78]时,出现值为feq+[0.20;0.10]的干扰;k≥122时,出现值为feq+[1;-1]的干扰。其他时段内干扰为feq。YolN(00)=[yeq;…;yeq]。取yeq=0、ueq=0和feq=0。下面采用线性规划,给出SSTC的所有优化问题,其中为书写简便,没有完全采用规则r1~r12进行简化。
优先级1:
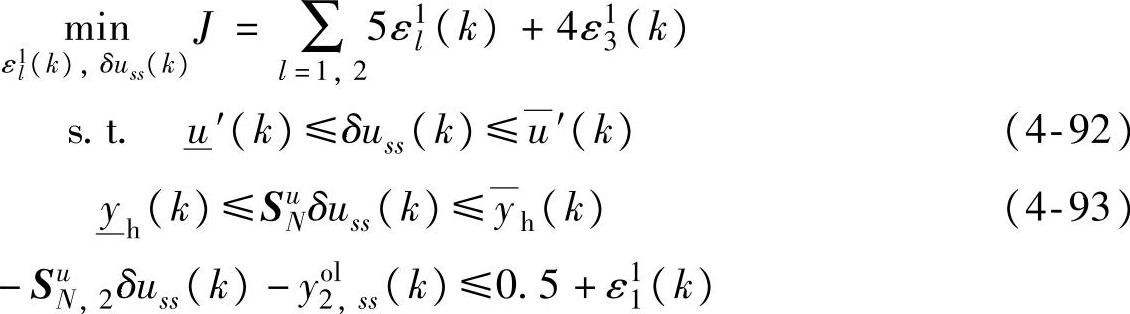 (https://www.xing528.com)
(https://www.xing528.com)
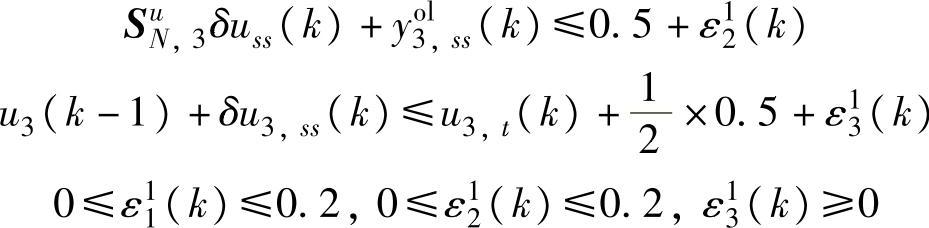
优先级2:
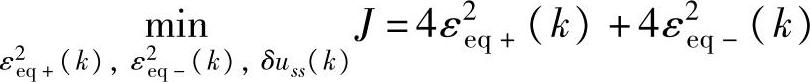
s.t.式(4-92),式(4-93)
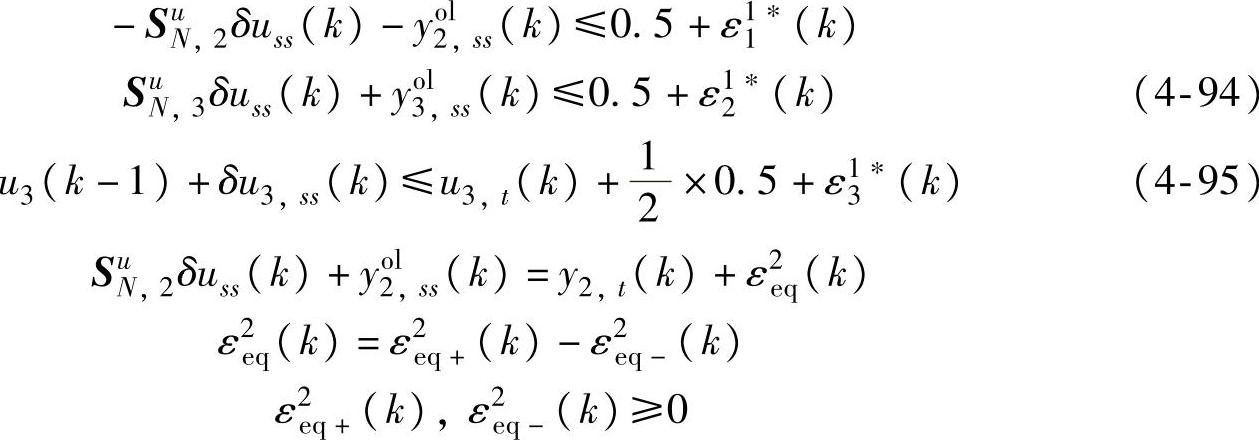
优先级3:

s.t.式(4-92),式(4-94)~式(4-95)
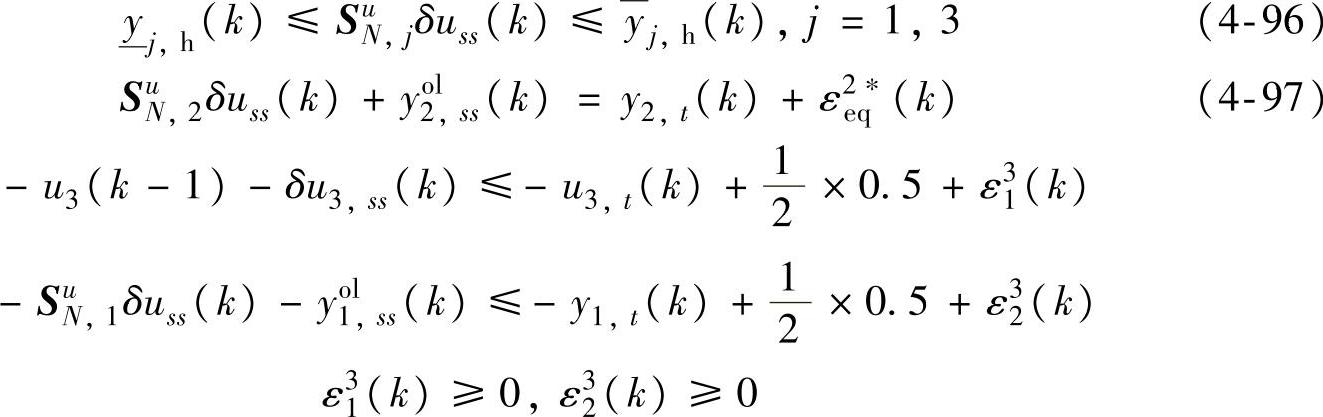
优先级4:

s.t.式(4-92),式(4-94)~式(4-97)

优先级5:
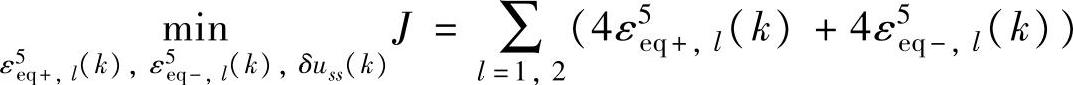
s.t.式(4-92),式(4-94)~式(4-99)
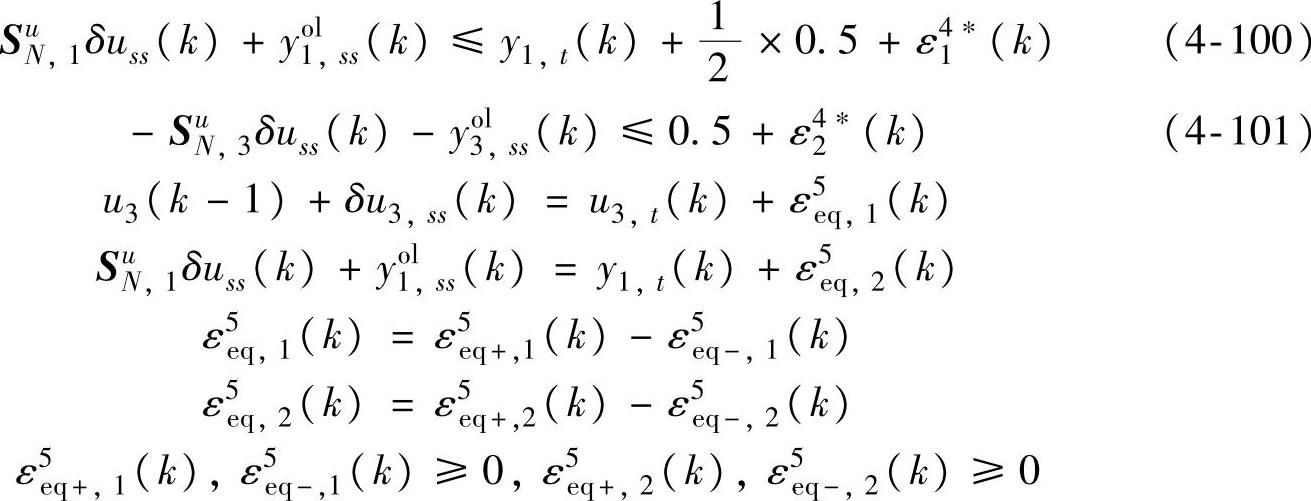
经济化优阶段(最低优先级软约束不起作用):
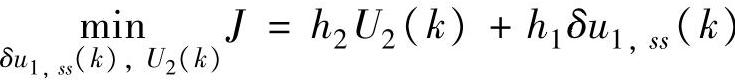
s.t.式(4-94),式(4-97)~式(4-101)

表4-1 多优先级SSTC参数选取

(续)

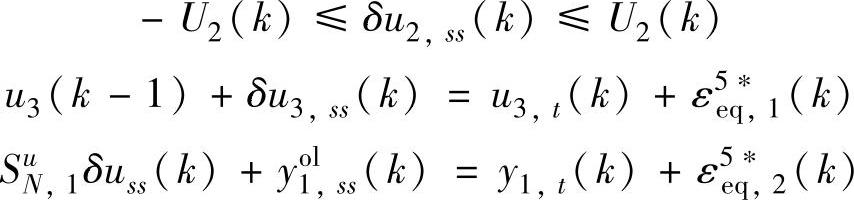
选择P=15,M=8,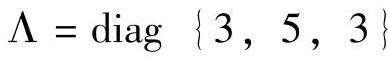 ,
, ,
,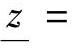
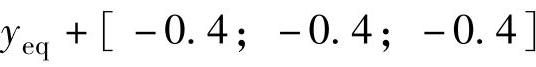 ,
, ,
, ,
,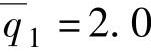 ;
;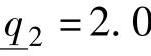 ,
, ,
, =2.0;
=2.0;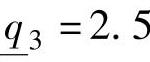 ,
,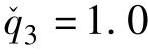 ,
,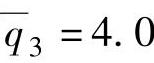 ,ρ=0.2。u(-1)=ueq,y(0)=yeq,Δu(k)=Δu(kk)。真实系统输出用MATLAB SIMULINK利用以上传递函数矩阵产生,并乘以0.9来代表模型与实际系统失配。SSTC可行性阶段采用LP,经济优化阶段采用QP时,动态控制结果见图4-2,表明SSTC层给出的CV和MV的稳态值可以被动态控制层完全跟踪上。
,ρ=0.2。u(-1)=ueq,y(0)=yeq,Δu(k)=Δu(kk)。真实系统输出用MATLAB SIMULINK利用以上传递函数矩阵产生,并乘以0.9来代表模型与实际系统失配。SSTC可行性阶段采用LP,经济优化阶段采用QP时,动态控制结果见图4-2,表明SSTC层给出的CV和MV的稳态值可以被动态控制层完全跟踪上。
注意在本例中,取其他任意{y,u,f}eq(不需满足yeq=SuNueq+SfNfeq)时可能仍然可行。如果所取的{y,u,f}eq满足yeq=SuNueq+SfNfeq且不存在模型失配,则对不同的{y,u,f}eq,仿真结果仅是绝对数值不同、相对变化(即曲线形状)不会改变。这些结果已经得到仿真验证,此处略。
在本例中,如果模型不变,而对产生真实系统输出的传递函数矩阵做如下修改:
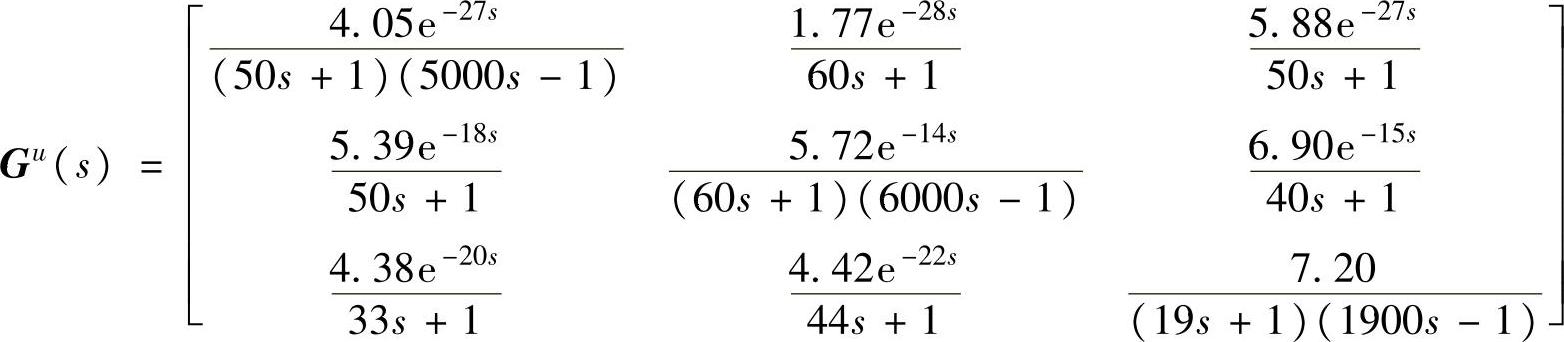
则闭环系统未能镇定;如果模型不变,而对产生真实系统输出的传递函数矩阵做如下修改:
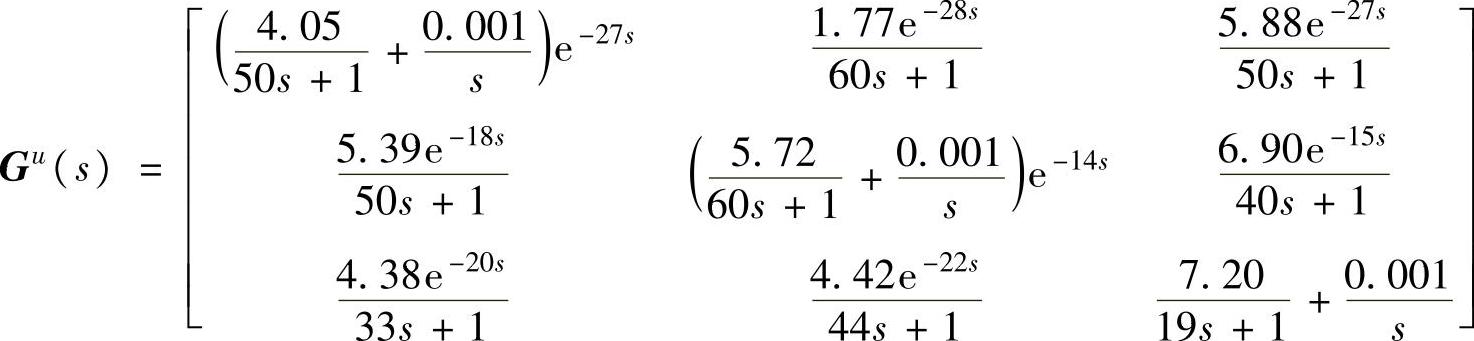
则闭环系统能够镇定。如果产生真实系统输出的传递函数矩阵不变,而阶跃响应模型做如下改变(斜坡):
Sui←Sui(1+0.01i),Sfi←Sfi(1+0.01i)
则闭环系统能够镇定;如果产生真实系统输出的传递函数矩阵不变,而阶跃响应模型做如下改变(翘尾):
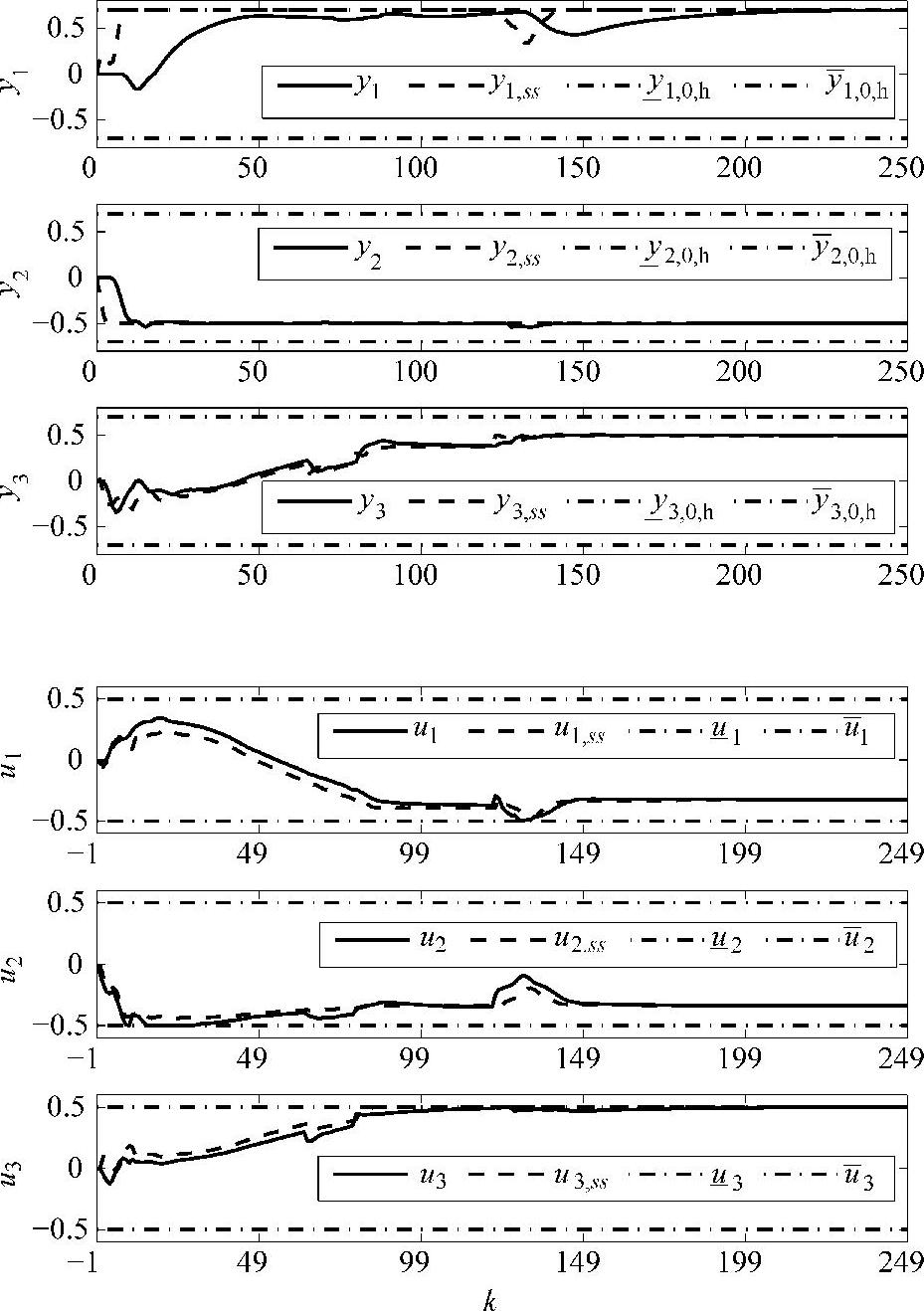
图4-2 控制效果图
Sui←(1+0.01e0.01i)Sui,Sfi←(1+0.01e0.01i)Sfi
则闭环系统能够镇定;如果产生真实系统输出的传递函数矩阵不变,而阶跃响应模型做如下改变(拖尾):
Sui←(1-0.01e0.01i)Sui,Sfi←(1-0.01e0.01i)Sfi
则闭环系统能够镇定。以上能镇定的情况需要修改一些参数。针对一系列仿真,总结如下:
系统不可不稳定,模型可以不稳定;
系统可以有积分,模型可以有积分。
注解4.11 从前面的叙述中可以看出SSTC既有LP方法也有QP方法,而目前主流的MPC工业技术大都采用QP来求解动态控制问题。SSTC和动态控制都是需要求解约束优化的,但是两者的问题规模是不一样的,后者的计算量通常大得多。如果生产单元的规模很大,可能造成动态控制的计算时间超出控制周期、MPC无法得以实施。对于这类大规模的多变量控制问题,工程上的解决方案是按照一定的工艺特点,将某些输入输出变量组合在一起,采用多个独立的MPC完成整个单元的控制。这样的多MPC控制方案如果设置得当,也可以取得较好的控制效果,但是这种配置忽视了生产装置之间的上下游关系,无法使控制系统获得更好的性能。
某些MPC工业技术使用组合SSTC策略(名字参考文献[46]第4页注脚CLP)来解决这个问题,具体的策略:将较大规模的被控过程分解为多个被控子过程,每个子过程配备一个动态控制器。在全过程模型的基础上执行SSTC,并将计算结果分别下传到各动态控制器作为它们的设定值,各动态控制器分别利用各自的子过程数学模型进行动态优化计算。由于SSTC的计算量比动态控制的计算量要小得多,采用这种方法可以在有限时间内对更大范围的生产过程进行稳态优化。此外,某些动态控制器还可将其他一些动态控制器的预测输出作为前馈。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




