稳态目标计算的可行性阶段

在每个优先级的优化问题中，必须满足如下的硬约束：

约束式（4-54）是由式（4-15）～式（4-18）组成的。另外，将该优先级之前所有优先级的约束（可能已经放松）作为硬约束，而将该优先级的软约束放松，最终使得优化后的约束集是相容的。考虑优先级r（较大的r对应较低的优先级）。记通过第r个优先级的优化问题的求解，得到的从第1级到第r级软约束的处理结果为

约束式（4-55）～式（4-56）相对于第r+1个优先级的优化而言，是硬约束，即在求解第r+1个优先级的优化问题时，式（4-55）～式（4-56）必须满足。

易知，式（4-55）由如下一些约束组成：

而式（4-56）由如下一些约束组成：

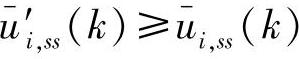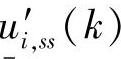
其中，在具体应用时各个集合的生成需要细化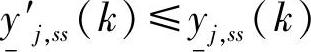，，；，；，；，。式（4-57）～式（4-64）分别是式（4-19）～式（4-20）、式（4-23）～式（4-24）、式（4-27）～式（4-30）放松后的结果。

引理4.1 在式（4-57）～式（4-64）的作用下，式（4-54）被简化为

证明：原理同前面的r1～r12。

证毕

以上引理4.1表明，在求解第r+1个优先级的优化问题时，式（4-54）可以由式（4-65）～式（4-68）代替。因此，在第r+1个优先级中，考虑的约束为式（4-65）～式（4-68）和(www.xing528.com)

其中，ε^（r+1）（k）和ε^（r+1）_eq（k）为松弛变量，对ε^（r+1）_eq（k）的要求应为绝对值越小越好。

对第r+1个优先级的优化问题，或者采用线性规划，或者采用二次规划。如果在一个优先级中，要同时调整多个等式/不等式型软约束，则对它们给予同等重要的关注。对每一个标量松弛变量ε，记其对应的等关注偏差为。对y_j，ss（k）所涉及的CV上界软约束，可以取其等关注偏差为；对y_j，ss（k）所涉及的CV下界软约束，可以取其等关注偏差为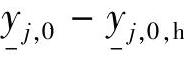。对ET对应的上/下界和等式软约束，可以取其等关注偏差为，其中，对u_i，t（k）和y_j，t（k）分别为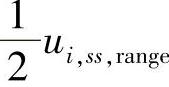和。下面分两种情况讨论。

（1）线性规划。令

其中，ε^（r+1）_eq+（k）和ε^（r+1）_eq-（k）为松弛变量。则求解

s.t.式（4-65）～式（4-68），式（4-69），式（4-70）其中，下角标τ表示对应于ε^（r+1）_eq（k）的第τ个元，而d^（r+1）_eq表示ε^（r+1）_eq（k）的维数；下角标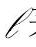表示对应于ε^（r+1）（k）的第个元，而d^（r+1）表示ε^（r+1）的维数。

（2）二次规划，则求解

s.t.式（4-65）～式（4-68），式（4-69）

当第r+1个优先级的优化完成后，式（4-69）则被表达为式（4-55）～式（4-56），其中，式（4-55）～式（4-56）中的r被替换为r+1。