【摘要】：通过对不等式约束引入一系列辅助变量χ≥0，并对软约束同时引入松弛变量ε≥0，可以将式～式，式～式，式～式化成等式约束的形式，如下：由式得到，并代入式、式、式、式、式、式。由式得到，并代入式、式、式、式。以上将不等式约束化成等式约束的做法见参考文献[83]，适合于直接在单纯形法LP中采用。
通过对不等式约束引入一系列辅助变量χ≥0，并对软约束同时引入松弛变量ε≥0，可以将式（4-15）～式（4-20），式（4-23）～式（4-24），式（4-27）～式（4-30）化成等式约束的形式，如下：
由式（4-31）得到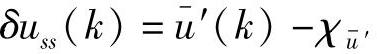
，并代入式（4-33）、式（4-35）、式（4-37）、式（4-39）、式（4-41）、式（4-42）。由式（4-32）得到
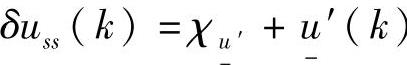，并代入式（4-34）、式（4-36）、式（4-38）、式（4-40）。将式（4-31）与式（4-32）相加。从而得到
在后面的讨论中，统一采用原来的约束式（4-15）～式（4-20）、式（4-23）～式（4-24）、式（4-27）～式（4-30），但也可以采用式（4-43）～式（4-53）得到相同的计算结果。若采用式（4-43）～式（4-53），则决策变量δuss（k）被替换为χ；约束式（4-43）～式（4-53）分别对应式（4-16）～式（4-20）、式（4-23）～式（4-24）、式（4-27）～式（4-30），而式（4-15）被移除[在得到
后，可计算
，相当于利用了式（4-15）]。(www.xing528.com)
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
