开环动态与稳态预测值的优化方法

在第2章，基于FSR模型的状态空间表示已经给出了用Kalman滤波求解开环预测的方法。记k时刻的开环动态预测值如下：

一般取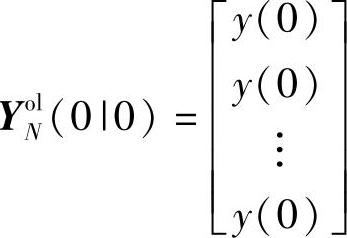作为初值。在k＞0时刻，检测到Δu（k-1）的实际值后，根据式（4-2）可计算出

y^ol（k|k）=y^ol（k|k-1）+S^u₁Δu（k-1）

此处，上角标“fr”被改为“ol”。基于实测被控变量y（k）得

（k）=y（k）-y^ol（k|k）=y（k）-y^ol（k|k-1）-S^u₁Δu（k-1） （4-4）

该ε（k）反映了阶跃响应模型中未包含的不确定因素对稳定型CV的影响，称为预测误差。由于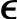（k）可能包含了噪声的影响，可对其进行滤波处理，以一阶惯性滤波为例，得到

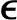′_j（k）=α_jj（k）+（1-α_j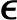）′_j（k-1），k＞0，′_j（0）=_j（0）

其中，α_j∈（0，1]为平滑系数（读者可考虑一阶惯性滤波下如何用Kalman滤波解释）。采用′_j（k）进行反馈校正，并且取反馈校正对未来所有时间点都是恒定的，即

e（k+i|k）=′（k），i≥0 （4-5）

这相当于假设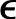′（k）为输出端阶跃型干扰，对稳定型CV通常是合适的。综合式（4-2）和该反馈校正，得到(https://www.xing528.com)

其中，。式（4-6）称为开环动态预测方程。注意在式（4-2）中没有考虑反馈校正，而在式（4-6）中则考虑了反馈校正。

由于采用了式（4-5），故开环稳态预测为

y^ol_ss（k）=y^ol（k+N+i|k），∀i≥0 （4-7）

注意推导式（4-6）时隐含地用到了关系式y^ol（k+N|k-1）=y^ol（k+N-1|k-1），这与式（4-7）中k替换为k-1的情形一致，也就是说以上开环稳态和动态预测没有矛盾（具有一致性）。采用式（4-5）满足了这种一致性的需求。

注解4.1 （k）反映了不确定性对开环预测的影响。根据参考文献[54]的说法，“一般来说，不确定性的来源可分为两类：不可预知输入和不可预知动态”，它们分别表示了没有在模型中考虑的独立变量和建模不准确性的影响。

注解4.2 如果在k时刻还能预测未来干扰的变化，记为

则为了其后的SSTC和动态控制，要替换{Y^ol_N（k|k），N}如下：

其中

采用本章的开环预测的好处是在SSTC和动态控制模块中不需要再考虑干扰的影响。