详解二次规划算法

考虑的二次规划问题为

其中，H是n阶对称矩阵（Hessian矩阵）；c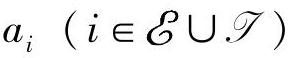，是n维列向量。优化问题共有m个约束，形成可行域记为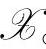。此时的问题就是在满足约束条件的集合（可行域）中寻找一点x^*使目标函数达到最小。

1.等式约束问题的解

等式约束二次规划问题可描述为

其中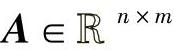，；b是m维列向量。假设A是列满秩矩阵（即A^T是行满秩矩阵）。对等式约束问题式（3-67），可求出解析解。

Lagrange方法

等式约束问题式（3-67）的Lagrange函数为

最优解的必要条件是

写为矩阵形式得

系数矩阵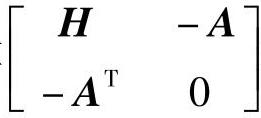称为Lagrange矩阵。如果它是可逆的，则方程组（3-70）有唯一解。

下面来导出方程（3-70）的求解公式。假设H和A^TH^-1A非奇异，则

因此，由式（3-70）可得解的表达式

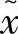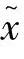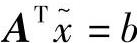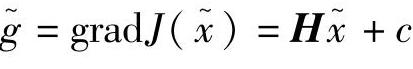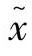下面给出另外一种表达式，设是问题（3-67）的任一个可行点，即满足。而在此点处的目标函数梯度为，利用和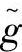，可将式（3-73）改写为

式（3-74）为等式约束问题（3-67）的唯一的最优解和Lagrange乘子。

2.有效集方法

本节对具有等式和不等式约束的二次规划问题的有效集方法进行叙述。首先给出有效集的定义：

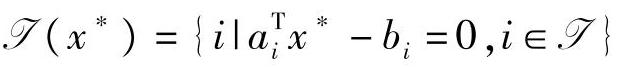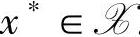定义3.1 记。对任意，称集合

是在x^*处的有效约束集或起作用的约束集，简称有效集。

二次规划问题的可行域是凸集，故当H为半正定时，它是一个凸规划问题，此时，任何局部最优解都是全局最优解。有效集方法是建立在下述结论之上的。

定理3.3 对式（3-66），设可行域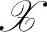非空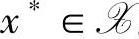，,x^*是全局最优解（K-T点）的充要条件是x^*满足K-T条件，即存在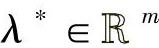使得

同时，还可以得到一个引理：

定理3.4设x^*是式（3-66）的可行点，如果x^*是下述问题

的K-T点，且相应的Lagrange乘子λ^*满足

则x^*是式（3-66）的K-T点。

有效集方法是一种迭代算法，在每次迭代中，都以问题可行点为起点，把在该点的有效约束按照等式约束处理，而把在该点的非有效约束暂时去掉不考虑，这样，把问题转化为仅带等式约束的二次凸规划问题来求解。求得一个新的更好的可行点，再重复以上步骤，经过有限次迭代就可求得凸二次规划问题的最优解。

第一步：形成子问题，并求解。设在迭代的第k步，已知可行点x_k，在该点的有效集为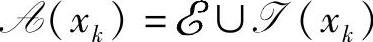，考虑子问题(https://www.xing528.com)

为方便起见，将原点平移到x_k，即令δ_k=x-x_k，代入式（3-78）并去掉目标函数中的常数项，得等价的子问题

其中，c_k=c+Hx_k，用求解等式约束二次规划问题的方法求出上述问题的最优解δ_k。

第二步：δ_k=0。这表明x_k是等式约束问题（3-78）的K-T点。计算相应的Lagrange乘子λ_i。如果对任意，λ_i≥0，则由定理3.4知，x_k是原问题（3-66）的K-T点。

如果存在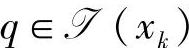，使得λ_q＜0，则x_k不是原问题（3-66）的K-T点。这时，如果在问题（3-66）中去除约束a^T_qx=b_q，则其后的任意可行点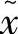满足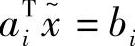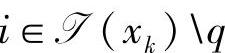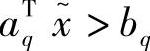：，，。因此，应该让q退出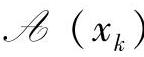，然后转到第一步。

第三步：δ_k≠0。需要分两种情况进行讨论。

（1）当x_k+δ_k是问题（3-66）的可行点时，取x_k+₁=x_k+δ_k；

（2）当x_k+δ_k不是问题（3-66）的可行点时，令x_k+₁=x_k+α_kδ_k，使x_k+₁为可行点。

下面研究如何求解步长因子α_k。因为时，对于任意的α_k都有a^T_iδk=0和a^T_i（x_k+α_kδ_k）=a^T_ix_k=b_i，所以问题的关键为如何满足

对情况（1），必有a^T_iδ_k≥0，且式（3-80）恒成立。对情况（2），必存在a^T_iδ_k＜0，故令

合并（1）～（2）两种情况可得

显然，α_k∈（0，1]。当α_k=1时，有效集不变；而当α_k＜1时，满足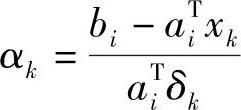的i也满足a^T_ix_k+₁=b_i，把此i加入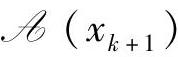，然后转到第一步。

根据上述分析，求解问题（3-66）的有效集方法的算法步骤总结如下：

（1）给定可行点x₀，令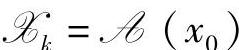，k=0。

（2）求解等式约束二次规划问题（3-79），得δ_k。如果δ_k=0，转步骤（3）。否则，

1）由式（3-82）计算α_k，令x_k+₁=x_k+α_kδ_k；

2）如果α_k=1，令；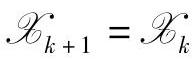

3）如果α_k＜1，求出使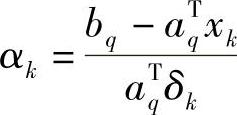的q，令；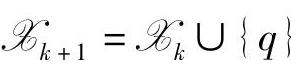

4）转步骤（4）。

（3）计算拉格朗日乘子λ_k=B_kg_k，其中，g_k=Hx_k+c，B_k=（A_kH^-1A^T_k）-1A_kH^-1，而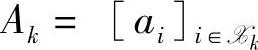。取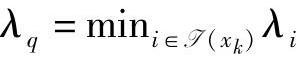。如果λ_q≥0，则x_k已是最优解，停止；否则，令。

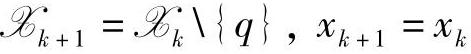（4）令k+1→k，转步骤（2）。

3.初始可行点的选取

初始可行点可以用线性规划得到。随便给，并确定τ_i=-sgn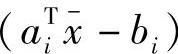，i∈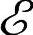。求解下列线性规划：

其中，e=[1，…，1]^T。得到的解记为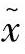。问题（3-83）总是可行的，它的一个初始可行点为

不难证明，如果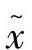是问题（3-66）的可行点，那么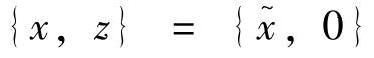就是子问题（3-83）的最优解；反之，如果问题（3-83）的最优值为0，则问题（3-66）有可行解。从而求解式（3-83）产生原问题的一个可行解。当然，该可行解可能离QP的最优解甚远。