优化软约束调整方法及可行性判定优先级

在工业生产中，各种约束的重要程度是不一样的，重要的约束要优先得到满足。采用以上的加权法，在某些情况下无论使用LP还是QP方法都会同时放松若干个软约束，虽然在一定程度上体现了某些软约束的重要性，但无法体现软约束的优先级特性。所谓优先级方法，是指在可行域为空时依据一定的次序来放松软约束^{[17，38，65，66，68，77-79]}。一个软约束所在的优先级（PriorityRank）表示了这个软约束的重要程度，优先级越高越重要。为了表达方便，为每个优先级定义一个级别数作为优先级的编号，并规定：级别数越小，优先级越高。不同的软约束的级别数可以相同也可以不同，同一个变量的上限和下限可以设置在不同的优先级。

过程控制中常见的软约束通常是与生产过程的某些要求相关联的，这些要求按照其重要性可由高到低排列为：安全或环保、积分CV界、模型验证、产品质量、经济性能。安全生产重于一切，可持续发展已经成为当前社会的主题，因而涉及环境保护的生产条件也是企业生产应首要满足的要求。积分CV的重要性在于其关系到MPC系统的稳定性，其越界是非常危险的，因而需要将积分CV的优先级设置为较高。模型验证涉及到在运行的模型是否有效（比如线性模型是与一定的稳态工作点相关联的），因此为了保证模型的准确度，这种软约束条件的重要性仅弱于积分变量。基于保证产品质量所提出的工艺要求，应尽量得到满足，但存在一定柔性（例如允许其在某一范围内波动）。出于经济性能的考虑对MV、CV的期望目标的设置，通常是一种更“软”的约束。

多优先级的做法非常普遍，在社会科学领域比比皆是。《西游记》小说的撰写，似乎遵循了多优先级，从高到低为：佛祖的法力无边；因果循环等佛学理论的宣传；西行的艰难；孙悟空的战斗力强；八戒等的成长等。因此，孙悟空也会受制于各种坐骑、动物演化的魔怪，这与其大闹天宫时的风格有很大不同。管理、人事领域多优先级的例子也很多。因此人们在科学技术中采用多优先级，确实算不上原创，只能算模仿了。

注解3.1 在优先级方法中，对“约束”一词的运用和变化比较多，因此需要首先明确几个概念。软约束是每个优先级所固有的，是随着优先级的确定而确定的。原始硬约束是SSTC所固有的、不允许软化的约束，是对每个优先级都要满足的。所谓某优先级的约束，是指该优先级的优化中要满足的约束，包括了原始硬约束、已经放松的软约束和未放松过的软约束。

当优先级确定后，形式上将每个优先级（假设共有r₀个优先级）的约束记为

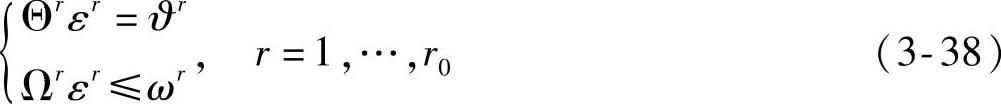
其中，上角标r表示优先级级别数。假设式（3-38）已包含ε^r≥0，并已经消除了ε^r以外的未知量，因此式（3-38）已经包含了所有的硬约束和相关软约束（可能已经放松）。可行性判定与软约束调整的优先级方法在实施过程中有升序和降序两种策略，下面分别介绍。

1.升序策略

基于升序策略的可行性判定与软约束调整的算法步骤为

步骤1：设置各软约束的优先级和权重系数。

步骤2：按照优先级级别数由小到大的次序逐级进行可行性判定与软约束调整。对于级别r，将所有级别数小于r的软约束（可能已经放松）作为硬约束。在级别r，进行可行性判定和软约束调整后，即考虑级别r+1。一直进行到所有r₀个优先级都进行了可行性判定和软约束调整为止。

下面，针对步骤2进行额外说明。考虑优先级级别数为1的情况，要考虑原始硬约束，并加入优先级1的软约束。优先级1的优化问题为

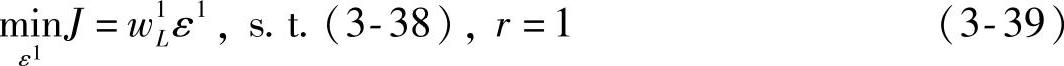
或

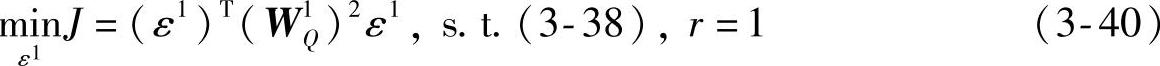
其中，w¹_L为元素皆正的权系数向量；W¹_Q为正定权系数矩阵。优先级1的优化问题可行的充要条件是原始硬约束集是相容的。

考虑优先级级别为2的情况。首先，要考虑原始硬约束、优先级2的软约束，并将优先级1的软约束（可能已经放松）作为硬约束，形成优先级2的约束。优先级2的优化问题为

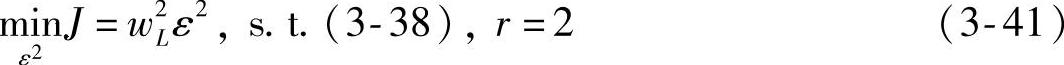
或

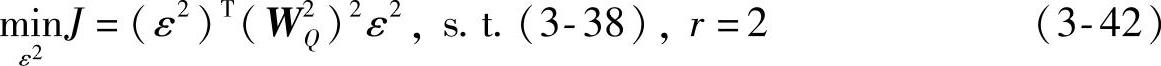
其中，w²_L为元素皆正的权系数向量；W²_Q为正定权系数矩阵。优先级2的优化问题可行的充要条件是优先级1的优化问题可行。

优先级3，…，r₀的情况，与级别2的情况相类似，这里不再赘述。升序策略具有递推可行性，即可行的充要条件是优先级1的优化问题可行。对于第r个优先级的优化结果，可做如下分析：若J=0，说明由优先级r的软、硬约束所构成的区域非空；若J≠0，说明由优先级r的软、硬约束所构成的区域为空，但将优先级r的软约束放松后所构成的区域非空。

通过上面的分析可知，所谓“升序”策略，是一种将软约束按照优先级级别数由小到大的次序，逐级“软”化变“硬”的过程。

2.降序策略

降序策略与升序策略相反，其判定与调整是根据优先级的级别数由大到小的次序进行的，而且它一开始就考虑全部的约束。基于降序策略的可行性判定与软约束调整的算法步骤为

步骤1：设置各软约束的优先级和权重系数。

步骤2：按照优先级级别数由大到小的次序逐级进行可行性判定与软约束调整。在优先级r，如果优化不可行，则将优先级r的软约束放松至最大允许量（比如，放松到工程约束），然后再考虑优先级r-1的优化；如果优化可行，则将优先级r的软约束按照最优解放松，不再进行优先级小于r的优化。对于优先级r，将所有级别数不等于r的约束（可能已经放松）作为硬约束。

下面，针对步骤2进行说明。考虑优先级级别数为r₀的情况。首先，要考虑所有级别数的软约束和原始硬约束，形成优先级r₀的约束。优先级r₀的优化问题为(www.xing528.com)

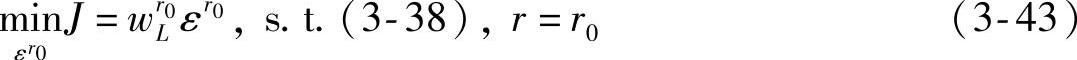
或

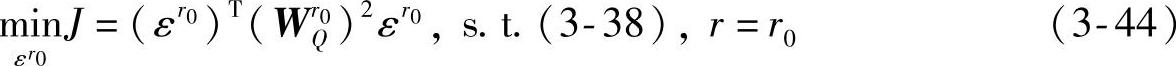
其中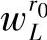，为元素皆正的权系数向量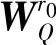；为正定权系数矩阵。可见，仅考虑对优先级r₀所对应的软约束进行放松，而其他级别的软约束作为硬约束处理。

如果在优先级r₀优化不可行，则需将优先级r₀的软约束放松至最大允许量，继续考虑优先级级别为r₀-1的情况。首先，要考虑所有级别数的软约束（可能已经放松）和原始硬约束，形成优先级r₀-1的约束。优先级r₀-1的优化问题为

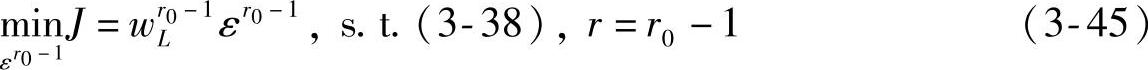
或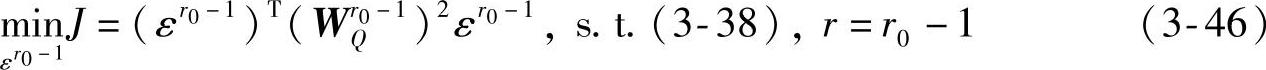

其中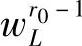，为元素皆正的权系数向量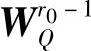；为正定权系数矩阵。可见，仅考虑对优先级r₀-1所对应的软约束进行放松，而其他级别的软约束（有的已经放松）作为硬约束处理。

优先级r₀-2，…，1的情况，与级别r₀-1的情况相类似，这里不再赘述。对于第r个优先级的优化结果，可做如下分析：若J=0，则说明所有的约束（包括已经放松的软约束、还未放松的软约束、原始的硬约束）形成了一个非空可行域；若J≠0，则说明所有的约束所构成的区域为空，但将优先级r的软约束放松后所构成的区域非空。降序策略进行到优先级1，如果优化问题仍然无解，则表明在允许范围内放松软约束不能形成非空可行域。

通过上面的分析可知，所谓“降序”策略，是一种将软约束按照优先级级别数由大到小的次序，由“硬”到逐级“软”化的过程。

注解3.2 特别注意，式（3-39）～式（3-46）的前提条件是未知变量（决策变量）只有本优先级的松弛变量，如果还有别的未知变量，则这些未知变量对应的硬约束都需要满足。另外，对每个优先级r，升序和降序策略的约束式（3-38）并不相同，并且该约束的具体参数是递推地在线更新的，而不是在设置优先级后（步骤1）就可以一次确定的。通常来说，消除松弛变量以外的未知变量未必降低计算量，故不一定要做到，因此式（3-39）～式（3-46）给出的只能属于原理性方法。

注解3.3 从“按照优先级次序最低限度地放松软约束”这个角度看，升序策略是最优的，降序策略并不是最优的。举例说明：假设约束的参数恰好使得只放松第2个优先级的软约束就可以了，这时降序策略会最大限度地放松所有优先级r＞2的软约束。但降序策略由于把软约束放得更松，有利于在经济优化中得到更大经济效益的解。另外，降序策略未必需要执行所有r₀个优化问题，所以与升序策略相比，可降低计算量。如果降序策略运行到r≠1后结束（可行域出现），则在优先级1～r，升、降序两种策略的结果是相同的，且在优先级1～r-1两种策略都无放松。

注解3.4 一种求解多优先级SSTC的方法可参考文献[44]和[73]（该书第93页），不是每个优先级求一个优化问题，而是所有优先级求一个混合整数规划问题。但混合整数规划问题的计算量通常是很大的。从“按照优先级次序最低限度地放松软约束”这个角度看，混合整数规划不可能比前述升序策略获得更好的效果。

注解3.5 席裕庚教授在“复杂工业过程的满意控制”（《信息与控制》，1995）一文中^[81]，提出了“满意控制”的概念。该文指出：“在复杂的工业环境中，由于存在各种软硬约束和多种目标要求，传统的自由度概念已不适用，传统的最优概念已被淡化，而代之以操作者对各种要求通过主观意识加以选择的满意概念”。满意控制的核心在于有约束多目标多自由度优化，包含了对硬约束、软约束、外部目标等的区别处理方式以及多优先级处理方法等^{[62，82，83，85]}，这与SSTC的思路是十分一致的。预测控制的SSTC应为满意控制的一个范例。SSTC的特点是每个控制周期自动进行（控制周期是分钟级的），人的参与一般只发生在MPC投运阶段，在MPC正常运行中进行的参数调整是有限的。满意控制的纵深发展可以与人机协调、计算机辅助设计等结合，属于工程优化方法的新概念。

例3.2 （见参考文献[95]）仍以Shell benchmark问题为研究对象，约定各MV约束界为[-0.5，0.5]，各CV操作约束界为[-0.5，0.5]，各CV工程约束界为[-0.6，0.6]，MV当前稳态目标为[0，0，0]，CV当前稳态目标为[0，0，0]，DV为[-1.7，-1.5]。以CV操作约束为硬约束进行SSTC，可知优化不可行，其原因在于过程受到了幅度较大的扰动的影响。在仿真中，将分别采用加权方法和优先级方法来进行软约束的调整。

（1）加权方法

为了说明权重对调整结果的影响，分别选取了七组参数（假设各CV上、下界的加权系数相同）来指示各CV约束的重要性。首先，采用LP方法，其计算结果见表3-1。其次，使用QP方法，其计算结果见表3-2。

可见，虽然基于LP的加权方法能够计算出使SSTC可行的CV约束界调整量，但软约束调整的结果不能完全反映出操作者设置权重的倾向性要求，这是因为软约束调整的结果是由权系数所构成的下降方向与多约束界相交的顶点共同决定的。基于QP的加权方法同样也无法反映出权重的要求，但与LP有所不同：即对CV约束条件的两个边界都进行了放松。

（2）优先级方法

这里，将CV1、CV2、CV3的约束上下界的优先级级别设为1、2、3。对于每一个CV约束的上下界，其权重的设置是相同的。

首先，根据升序策略进行计算。采用LP方法的计算过程及结果如下：第一步，对优先级级别1进行可行性判定，约束可行；第二步，对优先级级别2进行可行性判定，约束可行；第三步，对优先级级别3进行可行性判定，约束不可行，并调整CV3的上界，调整程度为ε_1，3=0.0172。采用QP方法的计算过程同LP方法一致，而且计算结果也一致（但这只是个特例，不具有通用性）。

其次，采用降序策略进行计算。采用LP方法的计算过程如下：对优先级级别3进行可行性判定（注意在升序策略中，对优先级1、2均不需要软约束调整，因此这里需要求解的问题完全等价于升序策略，所以结论相同），约束不可行，并得到ε_1，3=0.0172。QP方法同理。

表3-1 权系数选取与软约束调整对照表（LP）

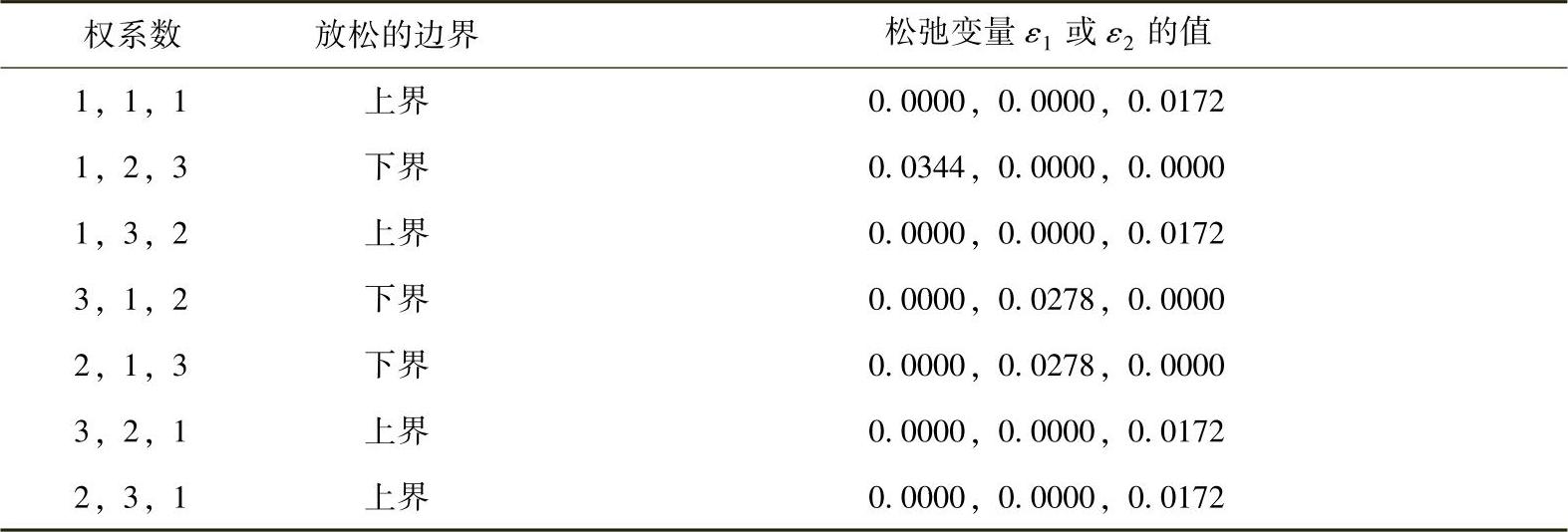
表3-2 权系数选取与软约束调整对照表（QP）

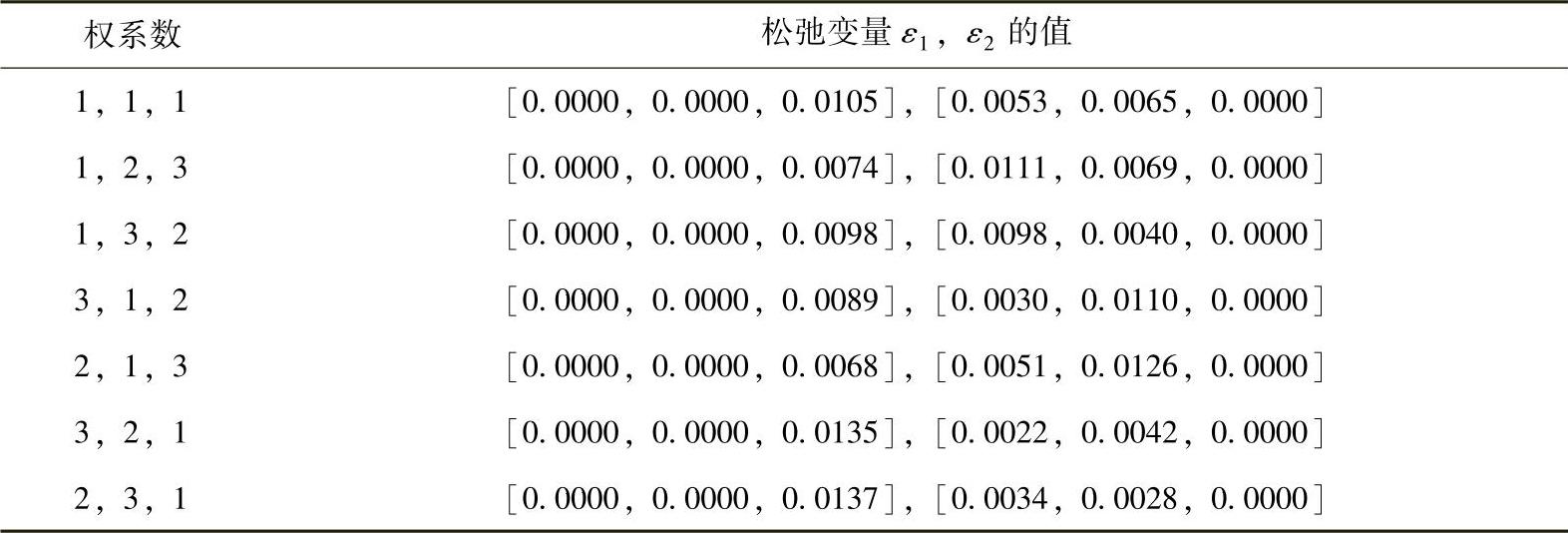
可见，基于优先级的软约束调整方法能够完全反映CV软约束调整时操作者的优先级意愿。