加权方法：可行性判定与软约束调整

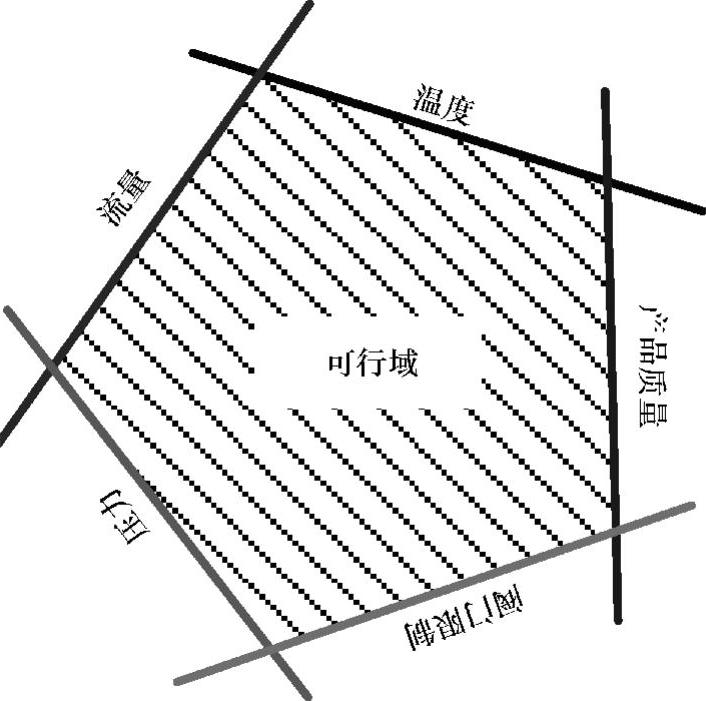
图3-4 多个约束条件构成的可行域

了解了什么是优化可行性，接下来就引出了两个问题，其一是优化可行性的判定问题，即根据过程的稳态模型及约束，判定优化问题是否可行；其二是软约束调整问题，即当判定结果为不可行时如何放松约束界使优化问题可行。只要适当地处理，则前一个问题可以合并到后一个问题。通常，可从软约束调整出发，通过计算得到的调整量来进行可行性的判定。

1.可行性判定与软约束调整方法的图解

首先，图解SSTC的不可行问题。以二维空间为例，每个约束界都可以划出一条直线，直线的一侧是可行的，多个约束条件划出多条直线。多条直线的可行侧能否框定一个非空的区域，这就是可行域的存在性（可行性）问题。如图3-4阴影部分所示，5个约束条件的可行侧构成了一个五边形的可行域。试想，如果其中一个约束条件的可行侧恰好与图3-4中的情况相反，那么现有的可行域就不存在了。

下面，以一简单的一输入两输出过程为例^[95]，来说明如何进行软约束调整以及如何利用软约束调整方法进行可行性的判定。假设稳态模型为

假设只需考虑如下约束

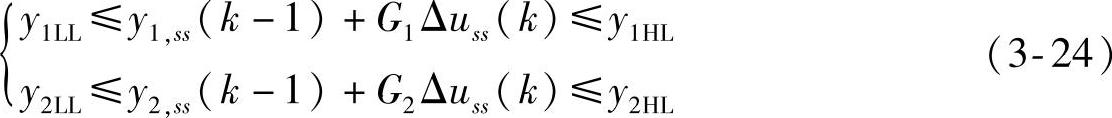
因为只有一个MV，式（3-24）最终可转变为如下的形式

或

其中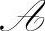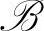，、是实数，且＜。显然，约束条件式（3-25）能够形成可行域，而式（3-26）不能。引入松弛变量ε₁≥0和ε₂≥0。由于松弛变量一般是直接施加在CV软约束上，所以需要引入整合参数α≥0和β≥0。经过软约束调整后，式（3-25）和式（3-26）分别变为

所谓软约束调整，就是在约束不可行时，通过最小程度地调整软约束界使约束变得可行。约束界的最小调整可以通过优化来完成，例如可将目标函数写作

J=λε₁+γε₂ （3-29）

其中，λ和γ是权重因子。由于式（3-27）和式（3-28）中包含Δu_ss（k），该变量对于软约束调整问题是一个未知量，可将Δu_ss（k）移除。对于式（3-27），只要将两个不等式相加即可实现Δu_ss（k）的移除，得到

对于式（3-28），同理得到

针对式（3-25）的情况，软约束调整的优化问题可描述为

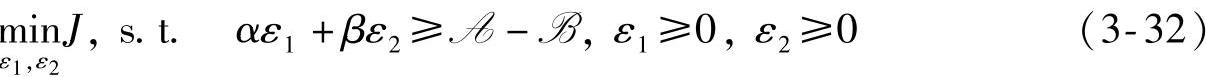(www.xing528.com)

这是一个LP问题，由于决策变量只有两个，因而可直接使用几何方法进行求解。因为α≥0，β≥0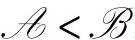，，可知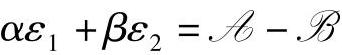这一直线与平面直角坐标系中ε₁轴和ε₂轴的交点都小于0。约束条件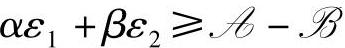包含了直线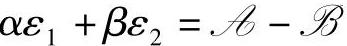上方的区域（如图3-5阴影部分所示），又由于ε₁≥0和ε₂≥0这两个约束条件，可行域为整个第一象限。因为软约束调整的优化目标是求取使λε₁+γε₂最小的ε₁和ε₂，可见最优点解即为原点，也就是ε₁=0、ε₂=0。具体情况，如图3-5所示。

针对式（3-26）的情况，软约束调整的优化问题可描述为

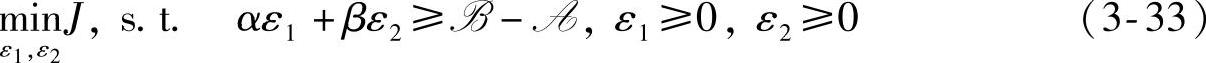
由于分析方法与式（3-32）相同，这里不再赘述。最终的可行域如图3-6阴影部分所示，是个由三条直线所围成的一个区域。由LP的特点可知，优化问题（3-33）的最优点一定位于直线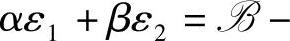与ε₁、ε₂轴的交点上，这两个点中哪个是最优点取决于λ和γ的取值。

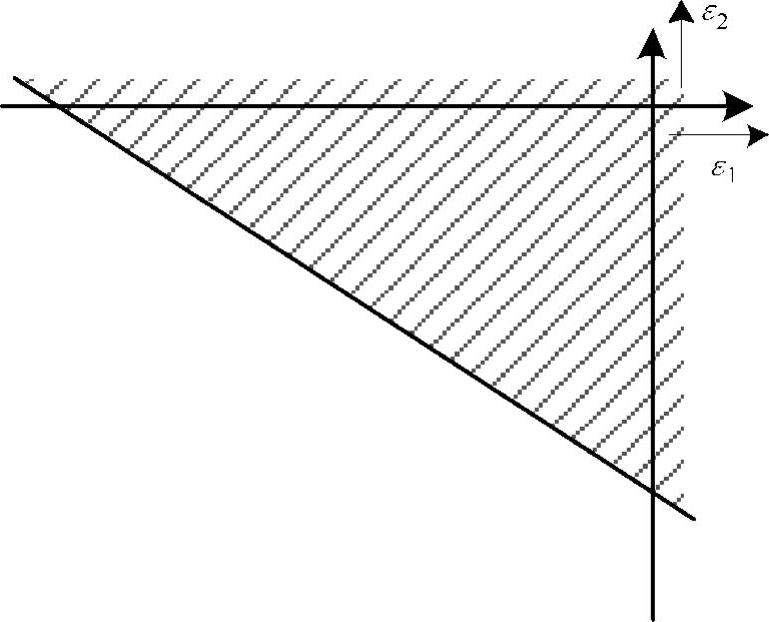
图3-5 SSTC不需软化约束时，软约束调整问题的可行域平面图

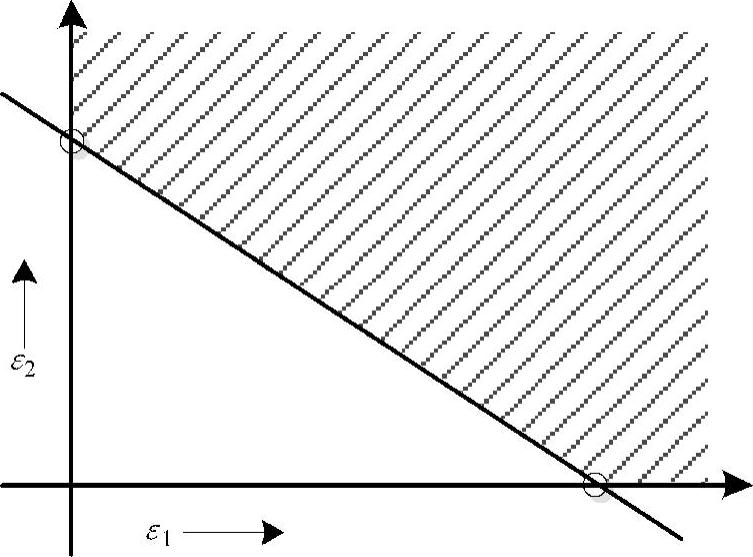
图3-6 SSTC需要软化约束时，软约束调整问题可行域平面图

更一般地，SSTC的优化可行性判定问题可合并到软约束调整问题。当松弛变量的最优解全为0时，说明约束无需软化即已存在可行域；当有非零解时，说明约束需要软化，且使用非零解进行软约束调整后获得可行域；如果无解，说明无法通过软约束调整的方法获得可行域。

2.可行性判定与软约束调整的加权方法

下面对约束条件进行规范化。当无需软化约束时，需满足

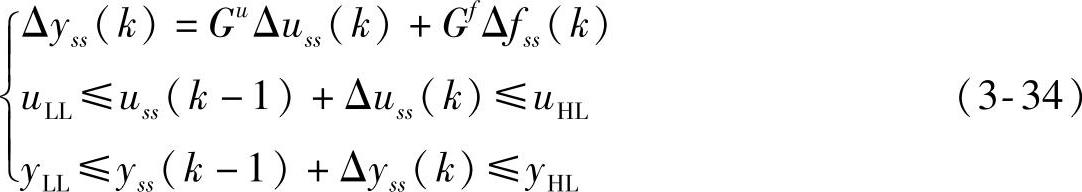
针对CV约束条件引入松弛变量，并将Δy_ss（k）的等式代入，得

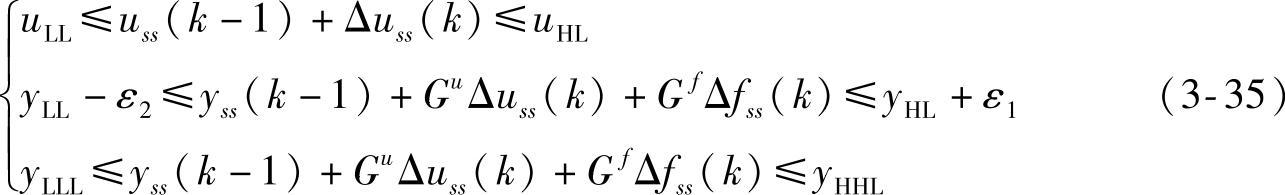
其中，ε₁、ε₂为CV约束条件的松弛变量，不含松弛变量的约束为硬约束。

通常，在进行软约束的调整时，可以通过权重来反映操作者的意愿。将式（3-29）中的目标函数推广为一般加权形式，得到如下的LP问题：

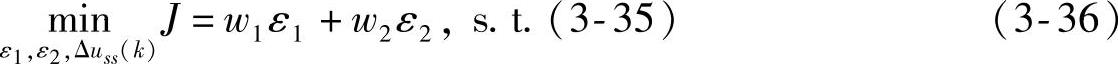
其中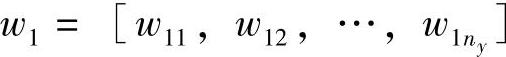，和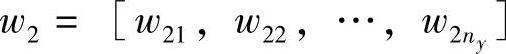的元素皆正。权系数w_ij的大小可反映松弛变量ε_ij的调整意愿。例如，调整ε_ij比调整ε_lt更易于接受，则相应w_ij＜w_lt；对于不希望调整的约束条件，相应的w_ij充分大。求解LP问题式（3-36）且优化可行时，可得到一组松弛变量ε₁，ε₂。

通过求解如下的QP也可实现软约束的调整：

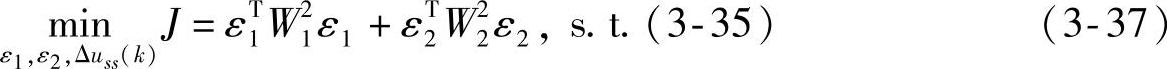
其中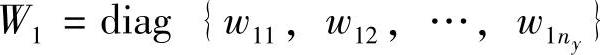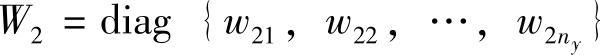，，皆为正定。

需要指出，LP和QP方法都可以进行软约束调整，但其结果一般是不一样的。这是因为在LP的求解过程中，一般不会使每个积极约束（积极约束是指起作用的约束，也称有效约束）都得到放松，而QP会。