经济优化方法：稳态目标计算

1.稳态目标计算的经济优化问题

在经济优化中，目标函数的设计应能够直接反映生产过程经济效益（包括收益和成本）。在经济优化中，常见的目标函数为（见参考文献[33，15]）

J=α^TΔu_ss（k）+β^TΔy_ss（k） （3-9）

目的是将MV与CV的变化所产生的收益最大化或成本最小化。由于Δu_ss（k）与Δy_ss（k）是线性相关的，所以式（3-9）中目标函数的MV、CV变化量可统一为MV变化量。

针对具体工程问题，首要工作是将MV单位变化量所产生的收益或成本标准化，然后使用标准化后的参量h来表示各MV的收益或成本，并使用符号“±”来区分成本与收益，“+”表示成本，“-”表示收益，因此目标函数应取最小化运算。如果MV的变化能够在一定程度上影响生产过程的收益或成本，这类MV在SSTC中被称为代价变量，与代价变量相区别的另一类MV是最小动作变量（关于最小动作变量的相关方法将在后续部分介绍）。最后，体现经济性能的目标函数变为

J=hΔu_ss（k） （3-10）

其中，。显然，h是根据各个MV的标准化收益或成本构建的代价系数向量，目标函数反映了MV发生变化后所产生的收益或成本变化。在SSTC的实施过程中，如何确定各MV的代价系数是个非常重要的环节。在MPC项目实施过程中，需要将过程经济特性和稳态输入输出关系一并进行考虑以估计MV的代价系数。在设置代价系数时要特别注意各MV的量纲，要把它们统一在某一个相一致的尺度上。

SSTC还需要考虑过程输入输出的稳态约束条件，即

其中，u_min和u_max分别为MV的下界和上界；y_min和y_max分别为CV的下界和上界。式（3-11）表示为

这样，经济优化问题可描述为一个LP问题

其中，Δy_ss（k）由式（3-5）代入。

SSTC经济优化问题也可以描述为一个QP问题。如果预先知道J的一个下界值J_min，就可以将目标函数改写为（hΔu_ss（k）-J_min）²，这样QP就向着经济性能最优的方向进行寻优了，而且由于LP与QP目标函数的下降方向是一致的，所以两者的最优解也必定相同。一般地，可这样求解J_min：如果h_i＞0，则代入Δu_i，ss（k）的下界，否则代入Δu_i，ss（k）的上界。

2.经济优化的最小动作问题

在工业生产中，某些MV的变化对经济效益的影响非常小甚至没有。如果作为代价变量，则代价系数过小。即使这些MV发生很大变化，对经济效益的优化的贡献也可忽略。此时较好的方案是对此类MV的动作（变化）进行惩罚，由此将这类MV称作最小动作MV。与代价变量一样，最小动作MV也存在代价系数，且该系数总是正的。针对具体问题，需要根据工艺要求来设置MV到底是代价变量还是最小动作变量。不失一般性，假设前n_mc个MV为代价变量，后n_u-n_mc个MV为最小动作变量。相应地，SSTC的目标函数为

J的前半部分体现经济效益。如果最小动作变量显著影响经济效益（即不是前面所说可以忽略），或者其通过约束影响J的前半部分，则不同的最小动作代价系数将产生不同的经济效益，此时，可先优化，然后固定代价变量的Δu_i，ss（k）、再优化得到最小动作变量的Δu_i，ss（k）。

以上目标函数中包含决策变量的绝对值形式，不利于优化问题的求解。通过引入辅助变量的方法可将绝对值形式转化为一般的标准型。令

|Δu_i，ss（k）|≤R_i（k），n_mc+1≤i≤n_u （3-15）

等价于

-R_i（k）≤Δu_i，ss（k）≤R_i（k），n_mc+1≤i≤n_u （3-16）

继而，目标函数改写为(www.xing528.com)

总之，最小动作问题可归结为如下的LP问题：

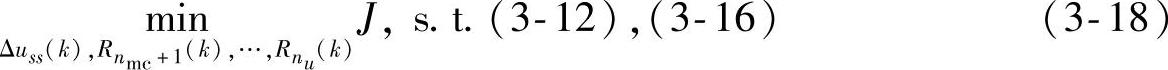
其中，Δy_ss（k）由式（3-5）代入。

例3.1 （见参考文献[95]）Shell重油分馏塔的控制是一个标准（bench-mark）控制问题，它的对象是一个多变量、有约束的系统，具有很好的代表性。重油分馏塔设备有三个产品抽出口，三个循环回流，如图3-1所示。经济目标函数和操作条件将决定分馏塔顶部和侧线抽出产品的浓度指标，底部产品无性能要求，但分馏塔底部有温度操作约束。三个循环回流通过热交换来达到产品分离的目的。所以，被控系统有变热负荷的性质，底部回流有一个焓控制器可以通过调整蒸汽量来达到调节热负荷的目的。

在平衡点附近，重油分馏塔的连续时间传递函数矩阵模型为

其中，MV包括顶部抽出流量u₁，侧线抽出流量u₂，底部回流量u₃；CV包括顶部产品浓度y₁，侧线产品浓度y₂，底部回流温度y₃；DV包括中段回流量f₁，顶部回流量f₂。系统各个变量已进行归一化处理，MV约束为[-0.5，0.5]，CV约束也为[-0.5，0.5]，为了便于观察MV、CV稳态目标的变化轨迹，取MV的单步稳态增量绝对值上限为0.2。

图3-1 重油分馏塔

容易得到系统的稳态模型为（与采样周期无关）

根据分馏塔的操作特性，可以设置各MV代价系数，令u₁、u₂和u₃的代价系数分别为-2、-1和+1，这是因为分馏塔的塔顶产品和侧线产品是塔的重要产物，过程优化要根据产品的价值合理分配塔的两种产品的抽出量，而热负荷的增加则在一定程度上增加了操作费用。需要指出的是，并不是与能源消耗相关的所有MV都有正的代价系数，如果能源来源于废热回收，或者企业能源供应非常充足，则此处的能量消耗可以不予考虑，即将代价系数设为0。

假设k=1时过程处于稳态，其中MV稳态值为（0，0，0），CV稳态值为（0，0，0）。下面，分几种情况，观察和分析SSTC的特点。首先，考虑不存在扰动的情况，经MATLAB仿真得到过程的稳态目标变化轨迹，由于存在增量约束的限制，最优稳态目标的到达是一个渐近的过程，如图3-2a、c所示，MV稳态目标值为0.5、0.2108和-0.4929，CV稳态目标值为-0.5、0.5和-0.4269。部分CV、MV稳态目标值到达约束条件的边界。对于基本的SSTC问题（MV为代价变量，CV为稳定变量），限制在约束界的稳态目标个数等于MV的个数。那么，SSTC的效果到底怎样？仅需观察SSTC前后的目标函数值即可得出结论。优化前的目标函数值为0，优化后的目标函数变化值为-1.7037，即通过SSTC增加了1.7037“份”效益。

其次，考虑扰动存在的情况下。假设f₁=0.2，f₂=0.1。过程的稳态目标变化轨迹如图3-2b、d所示，MV稳态目标值为0.5、0.1343、-0.5，CV稳态目标值为-0.2933、0.5和-0.4625，目标函数值变化了-1.6343。扰动使稳态目标发生变化，目标函数值稍逊于无扰动的情况，即由于扰动的影响使系统损失了一部分收益或增加了一些成本。

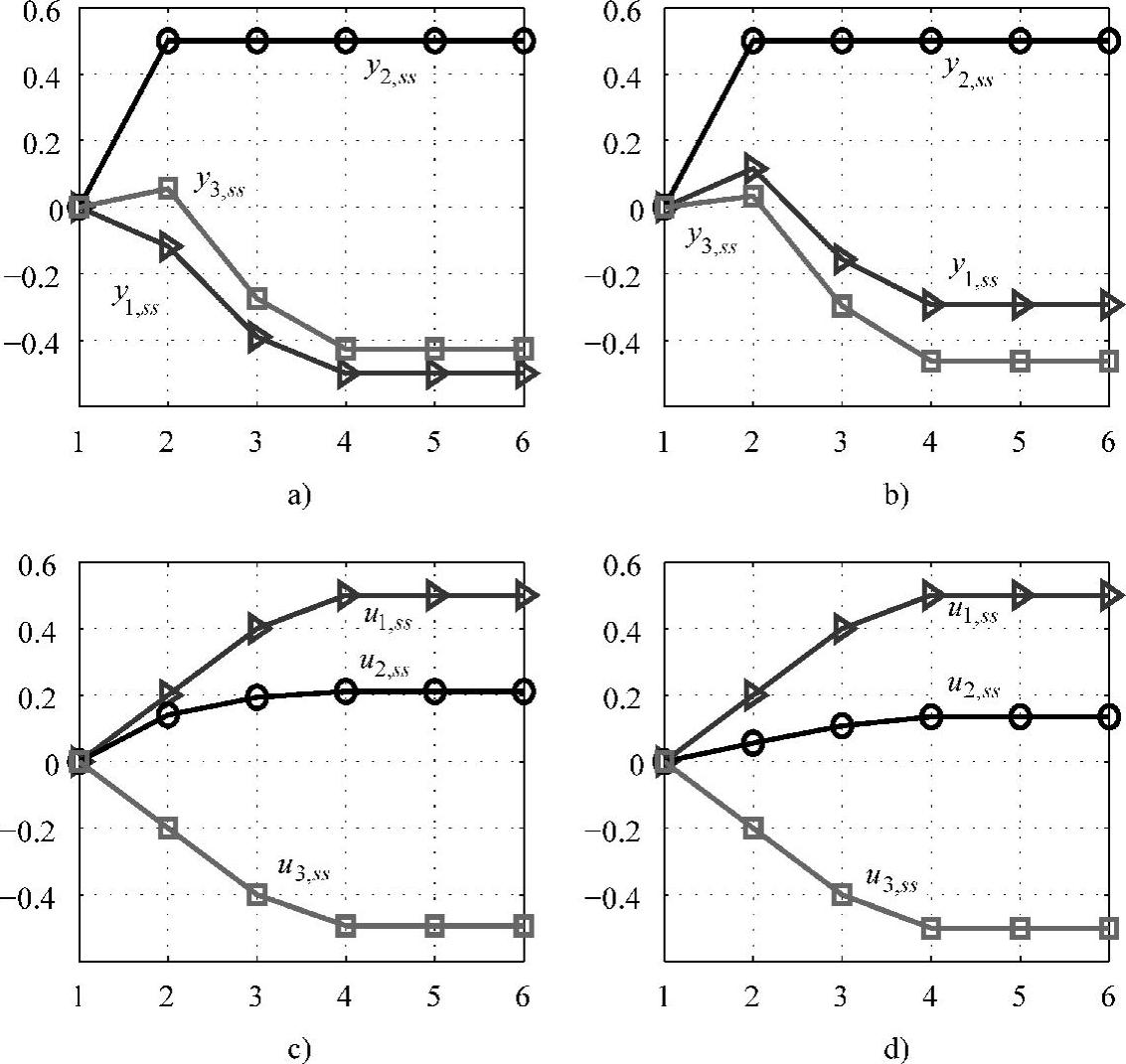
图3-2 稳态目标变化轨迹

a）、c）无扰动 b）、d）有扰动

下面，考虑存在最小动作MV的情况（无干扰）。令u₁和u₂为代价变量，u₃为最小动作变量。取u₁、u₂和u₃的代价系数分别为-2、-1和+2。经过计算得到如图3-3a、c所示的稳态目标变化轨迹，MV稳态目标值为0.5、-0.1113和-0.2259，CV稳态目标值为0.5、0.5和0.0719。由于最小动作代价系数并不大，所以在经济效益的驱动下仍然使最小动作变量发生了变化。再令u₃的最小动作代价系数为+10，经过计算得到如图3-3b、d所示的稳态目标变化轨迹，MV稳态目标值为0.1449、-0.0492和0，而CV稳态目标值为0.5、0.5和0.4175，这时改变最小动作变量的代价变得很大，因而实现了最小动作变量的不改变。

图3-3 含最小动作变量时的稳态目标变化轨迹

a）、c）最小动作变量代价系数较小 b）、d）最小动作变量代价系数较大