基于阶跃响应模型和Kalman滤波器的开环预测优化方法

对稳定CV，考虑如下的有限脉冲响应模型：

其中，上角标“s”表示稳定（stable），H^u，s_i和H^f，s_i分别为针对操作变量u和干扰变量f的脉冲响应系数矩阵。假设H^u，s_i=0，H^f，s_i=0，∀i＞N，而N为模型时域，N′≥N。由式（2-131）得到

由式（2-132）得到如下的有限阶跃响应模型（对所有N′≥N等价）：

其中，S^u，s_i和S^f，s_i分别为针对u和f的阶跃响应系数矩阵，满足S^u，s_N+i=S^u，s_N和S^f，s_N+i=S^f，s_N，∀i≥0。

在时刻k，在尚未得到Δu（k）时，假设已经得到Δf（k）。令y^s，fr（k+p|k）为Δu（k+i-1|k）=0，1≤i≤p和Δf（k+i）=0，1≤i≤p-1的情况下对y^s（k+p|k）的预测值，称为自由预测值，其中，上角标“fr”表示自由（free）。这些自由预测值满足y^s，fr（k+i|k）=y^s，fr（k+N|k），∀i≥N。采用式（2-133）进行预测得到

满足y^s，fr（k|k）=y^s（k）。(www.xing528.com)

对于一阶积分型CV，应该采用CV、脉冲响应系数、阶跃响应系数的增量，即式（2-131）和式（2-133）应该替换为

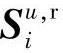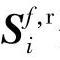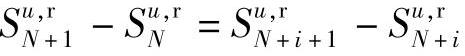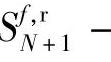
其中，上角标“r”表示斜坡（ramp，是对一阶积分的称呼）；N′≥N+1；H^u，r_i和H^f，ri分别为针对u和f的脉冲响应系数矩阵；和分别为针对u和f的阶跃响应系数矩阵。假设和，∀i＞N，故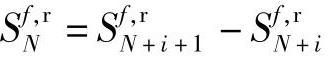，，∀i≥0。在式（2-135）两边不能去掉Δ，因为积分型CV不能表示为操作变量、干扰变量的有限项加权和。对应地，式（2-134）应该替换为

满足y^r，fr（k|k）=y^r（k）。式（2-136）等价于

因此，式（2-137）和式（2-134）具有统一的形式。积分型CV的自由预测值满足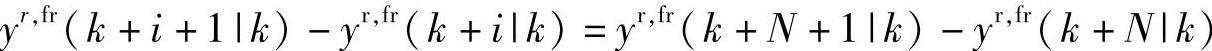，∀i≥N。