时变系统中的有色噪声和噪声相关性

考虑时变系统

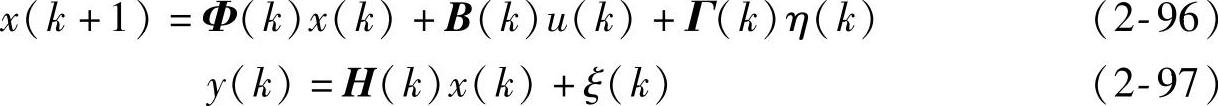
其中，Φ（k）、Γ（k）、H（k）和B（k）是已知的时变矩阵。

假设2.4 η（k）和ξ（k）满足

其中，Q（k）和R（k）是已知的时变矩阵。

定理2.8 在假设2.2～2.4下，时变系统式（2-96）～式（2-97）。有Kal-man滤波器

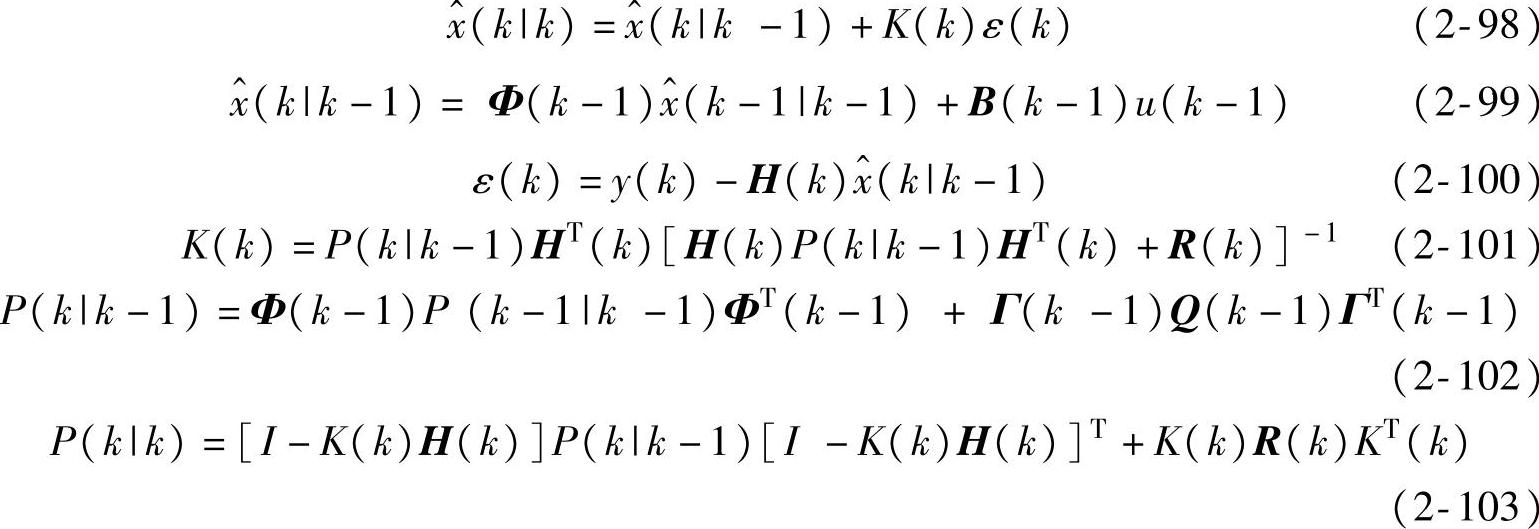
带初值式（2-50）。

此定理证明过程请参考定理2.5。利用式（2-102）～式（2-103）得到Riccati迭代公式：

式（2-86）是式（2-104）的特殊情况。在本节中，还要考虑η（k）和ξ（k）满足更一般的条件时，Kalman滤波器的相应结果，这些对深入考虑线性状态空间模型的预测控制和子空间辨识方法是必需的。

注解2.2 （输入噪声为有色噪声）考虑假设2.4不满足的一种情况，即η（k）为有色噪声。假设η（k）是具有有理谱密度的平稳随机过程，则根据谱分解定理（表示定理），可以描述为

η（k+1）＝Π（k）η（k）+η_c（k）

其中，η_c（k）满足

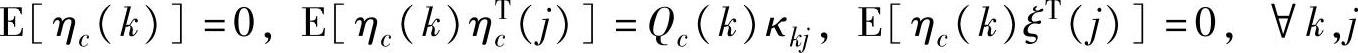
令，η^T（k）]^T，得到如下的增广系统：

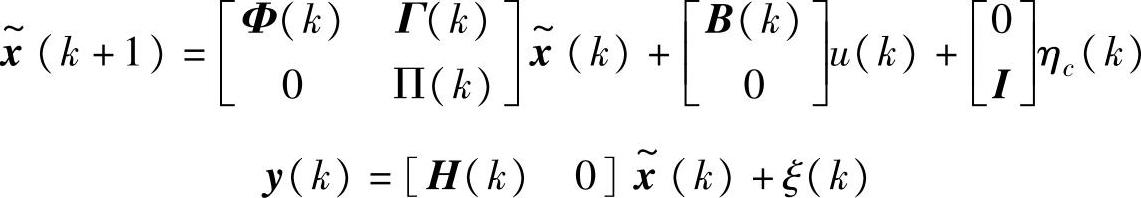
针对该增广系统的Kalman滤波器完全对照系统式（2-96）、式（2-97）。见参考文献[63]。

下面考虑假设2.4不满足的另一种情况：

假设2.5 η（k）和ξ（k）满足

其中，Q（k）、S（k）和R（k）是已知的时变矩阵。

在假设2.5下，由式（2-96）～式（2-97）得到^[2]

其中，。易知，对所有k、j满足E[η^*（k）ξT（j）]＝0，并且

E[η^*（k）η^*T（j）]＝Q^*（k）κ_kj，Q^*（k）＝Q（k）-S（k）R^-1（k）S^T（k）

针对式（2-105）与式（2-97）联立的系统，可适当依赖假设2.4，得到Kalman滤波器和预报器。

定理2.9 在假设2.2～2.3和假设2.5下，时变系统式（2-96）～式（2-97）有Kalman滤波器

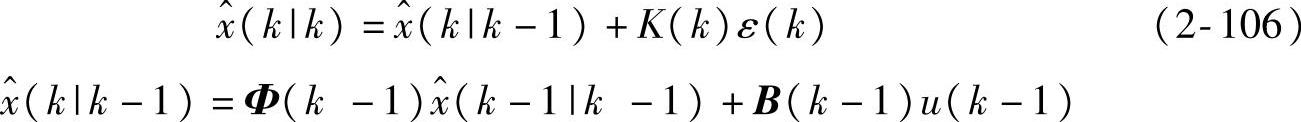
和Kalman预报器

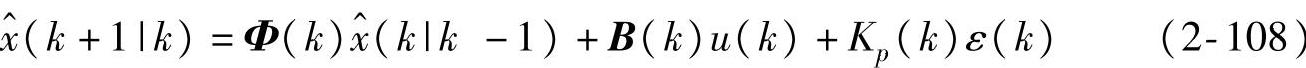
Kalman预报器带初值

(www.xing528.com)

和式（2-50）。在以上Kalman滤波器和预报器中，ε（k）见式（2-100），K（k）见式（2-101），且

而预报误差方差阵满足Riccati迭代

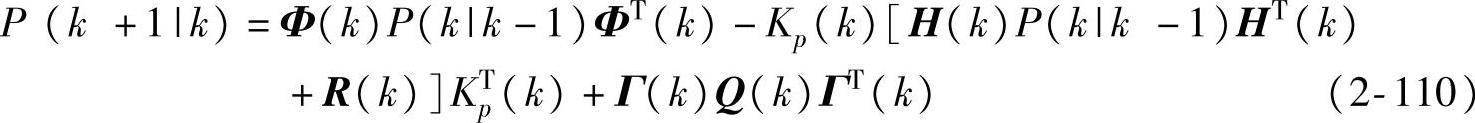
证明：用{[Φ（k）-Γ（k）S（k）R^-1（k）H（k）]，Γ（k）S（k）R^-1（k）y（k）+B（k）u（k）}代替{Φ（k），B（k）u（k）}，类似定理2.8可得到Kalman滤波器。用{[Φ（k）-Γ（k）S（k）R^-1（k）H（k）]，Γ（k）S（k）R^-1（k）y（k）+B（k）u（k），R（k），Q^*（k）}代替{Φ，Bu（k），R，Q}，类似定理2.6（推广到时变）可得到Kalman预报器，其中，P（1|0）和由Kalman滤波继承而来，推导中利用了一个关键的等式

利用该等式，并定义K_p（k）如式（2-109）所示，可以得到[Φ（k）-Γ（k）S（k）R^-1（k）H（k）]K（k）＝K_p（k）-Γ（k）S（k）R^-1（k）等。用{[Φ（k）-Γ（k）S（k）R^-1（k）H（k）]，Γ（k）S（k）R^-1（k）y（k）+B（k）u（k）}代替{Φ（k），B（k）u（k）}，推导可知：式（2-104）变成式（2-110）。

证毕。

注解2.3 （观测噪声为有色噪声）考虑假设2.4不满足的第三种情况，即ξ（k）为有色噪声。假设ξ（k）是具有有理谱密度的平稳随机过程，则根据谱分解定理（表示定理），可以描述为

ξ（k+1）＝F（k）ξ（k）+ξ_c（k）

其中，ξ_c（k）满足

定义

则根据式（2-96）～式（2-97）得到

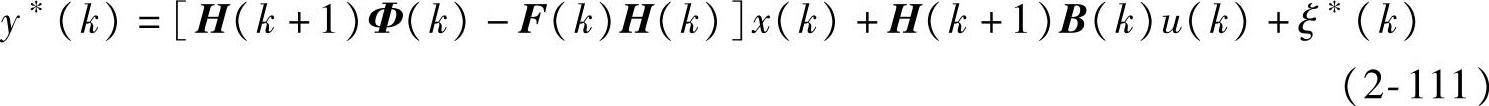
其中，ξ^*（k）＝H（k+1）Γ（k）η（k）+ξ_c（k）。易知

其中，S^*（k）＝Q（k）Γ^T（k）H^T（k+1），R^*（k）＝H（k+1）Γ（k）Q（k）Γ^T（k）H^T（k+1）+R_c（k）（见参考文献[2]）。

显然，这时满足假设2.5。定义y^**（k）＝y^*（k）-H（k+1）B（k）u（k），故

y^**（k）＝[H（k+1）Φ（k）-F（k）H（k）]x（k）+ξ^*（k） （2-112）

类似式（2-105）得到

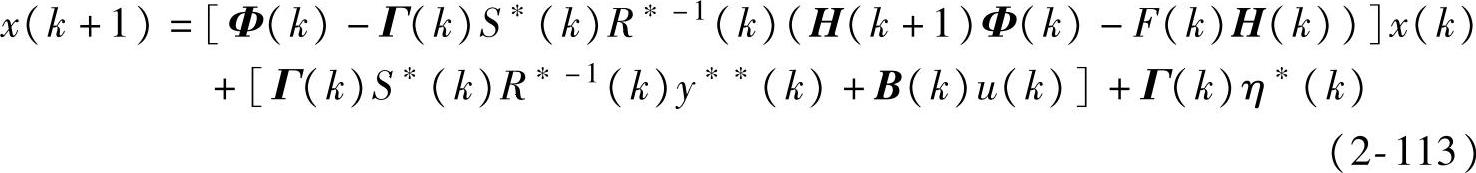
其中，。易知，对所有k、j满足E[η^*（k）ξ^*T（j）]＝0，并且

E[η^*（k）η^*T（j）]＝Q^*（k）κ_kj，Q^*（k）＝Q（k）-S^*（k）R^*-1（k）S^*T（k）

针对式（2-113）与式（2-112）联立的系统，可适当依赖假设2.4，得到Kalman滤波器和预报器。具体地，在k＞1时，利用y^**（k-1）＝y（k）-F（k-1）y（k-1）-H（k）B（k-1）u（k-1），相当于做k-1时刻的Kalman滤波和预报，得到和，因此这里得到Kalman滤波和预报结果总是有一步滞后。

由以上注解2.2、注解2.3和在假设2.5下的处理方法可知，关于η（k）和ξ（k）是互不相关白噪声的假设对线性系统并不是严苛的。

例2.4 考虑注解2.3中的Kalman滤波和如下的时变系统

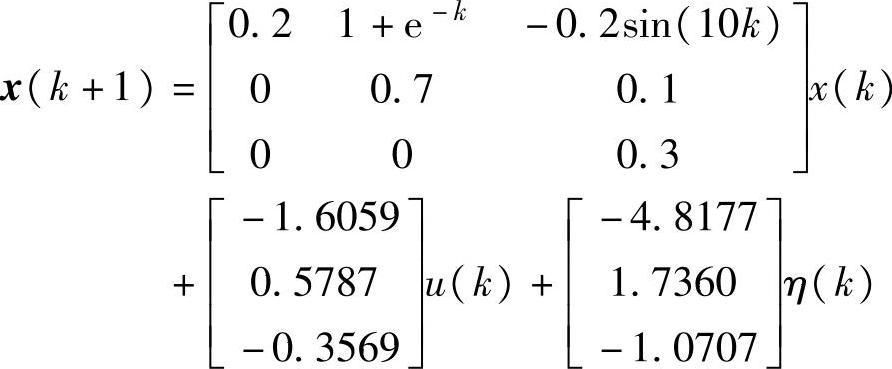
y（k）＝[-1.2193 1.8369 0.4253]x（k）+ξ（k）

其中x＝[x₁，x₂，x₃]^T，Q（k）＝1+0.5cos（k），R_c（k）＝0.75+0.25cos（1+k），ξc（k）和η（k）是具有相应方差的独立高斯白噪声，。取x（0）＝0，（0|0）＝0，ξ（0）＝0.3027，P（0|0）＝0。在u（k）＝0.3的输入作用下，仿真结果如图2-2所示，其中实线为真实值，虚线为估值。

图2-2 状态x（k）和Kalman滤波