【摘要】：由Kalman滤波器可得到如下Kalman预报器与超前m步预报器。定理2.6 系统式～式在假设2.1～2.3下，Kalman预报器为或其中，Kp称为Kalman预报器增益。预报误差方差阵满足Riccati迭代带初值P（1|0）＝ΦP（0|0）ΦT+ΓQΓT，和式。定理2.6中的P（1|0）和是由Kalman滤波器继承而来的。相应的m步预报误差方差阵为其中，P由式计算得出。证明：由式和投影性质有类似于式，有这引出proj（η（k+1）|y（1），…由式迭代m-1次有非递推关系上式减式引出因为，故由式可得式。
由Kalman滤波器可得到如下Kalman预报器与超前m步预报器。
定理2.6 （Kalman预报器）系统式（2-37）～式（2-38）在假设2.1～2.3下，Kalman预报器为
或
其中，Kp（k）称为Kalman预报器增益。预报误差方差阵满足Riccati迭代
带初值P（1|0）＝ΦP（0|0）ΦT+ΓQΓT，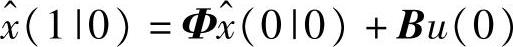
和式（2-50）。
由式（2-47）～式（2-49）得到式（2-86）。定理2.6中的P（1|0）和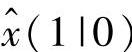
是由Kalman滤波器继承而来的。
定理2.7 （超前m步Kalman预报器）系统式（2-37）～式（2-38）在假设2.1～2.3下，超前m（m＞1）步Kalman预报器为
其中，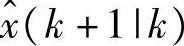
由定理2.6计算。相应的m步预报误差
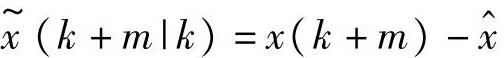（k+m|k）方差阵
为
其中，P（k+1|k）由式（2-86）计算得出。(https://www.xing528.com)
证明：由式（2-37）和投影性质有
类似于式（2-57），有
这引出proj（η（k+1）|y（1），…，y（k））＝0，因而有
同理有
用归纳法得式（2-87）。
由式（2-37）迭代m-1次有非递推关系
上式（2-94）减式（2-87）引出
因为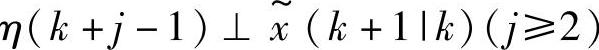
，故由式（2-95）可得式（2-89）。
证毕。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
