定理2.5 (Kalman滤波器)系统式(2-37)~式(2-38)在假设2.1~2.3下,Kalman滤波器为
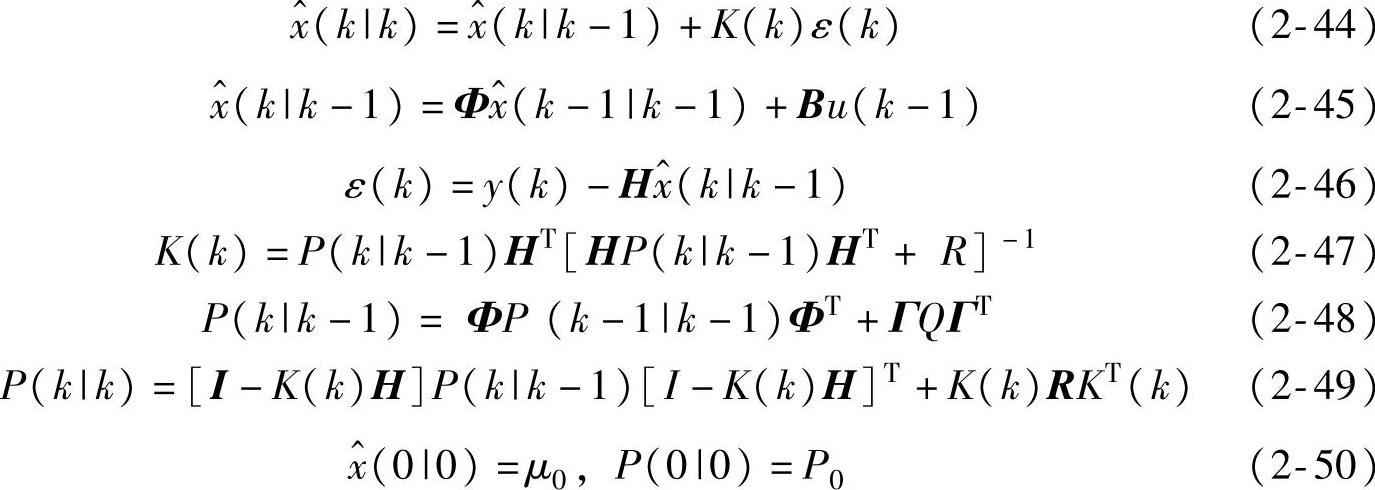
称K(k)为Kalman滤波器增益。
证明:在性能指标式(2-43)下,问题归结为求投影

由递推投影公式(2-36)得到递推关系式(2-44)和
K(k)=E[x(k)εT(k)]{E[ε(k)εT(k)]}-1 (2-52)
对k-1→k的状态方程两边取投影有
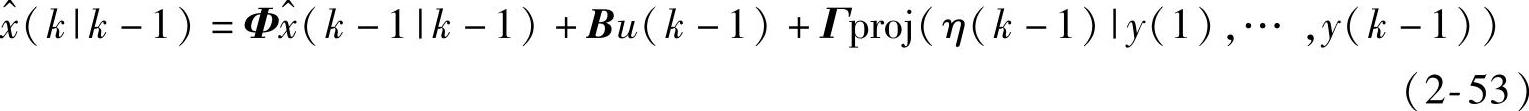
由状态方程迭代可知

且应用观测方程有
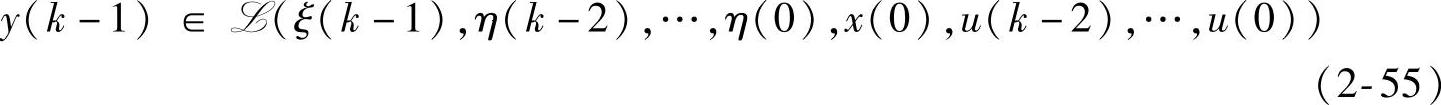
从而引出
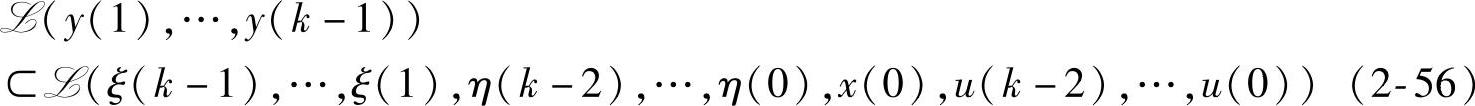
由式(2-56)、假设2.1~2.3有

故
proj(η(k-1)|y(1),…,y(k-1))=0 (2-58)
于是式(2-53)成为式(2-45)。
对式(2-38)取投影有
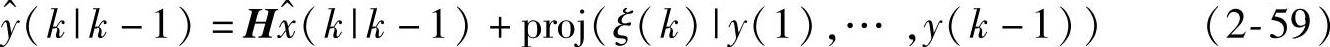
由假设2.1~2.3和式(2-56)有
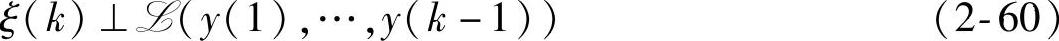
故
proj(ξ(k)|y(1),…,y(k-1))=0 (2-61)
于是式(2-59)成为

这引出新息表达式(2-46)。
记滤波和预报误差及方差阵为
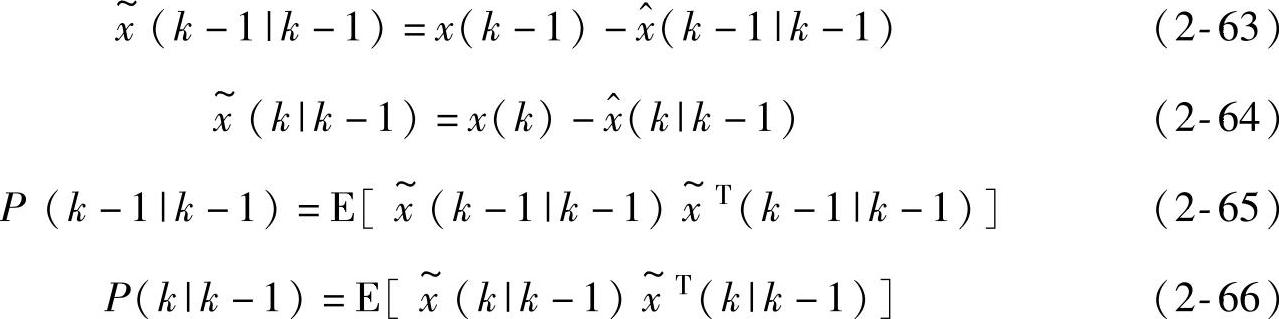
则由式(2-38)和式(2-46),有新息表达式
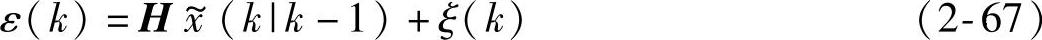
且由k-1→k的状态方程减式(2-45)得

由x(k)=x(k)减式(2-44)得
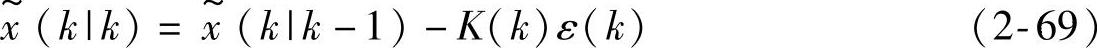
将式(2-67)代入式(2-69)引出
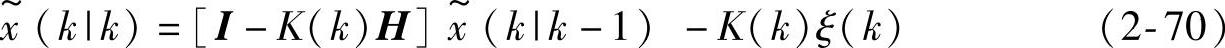 (https://www.xing528.com)
(https://www.xing528.com)
其中,I为单位阵。
因为

故有

这引出
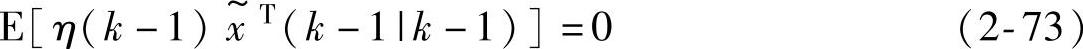
于是由式(2-68)得到式(2-48)。
因为
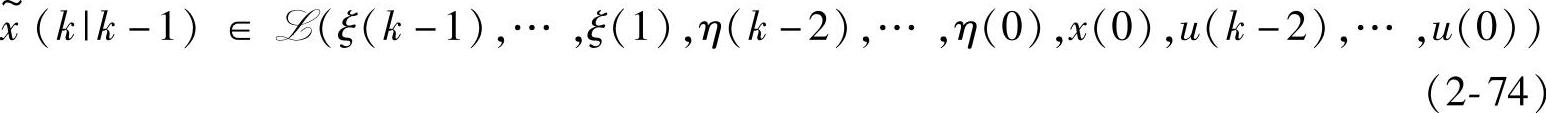
故有

由此引出

于是由式(2-67)得到新息方差阵为
E[ε(k)εT(k)]=HP(k|k-1)HT+R (2-77)
且由式(2-70)可得式(2-49)。
下面求Kalman滤波器增益K(k)。为此,求E[x(k)εT(k)]。应用式(2-67)有
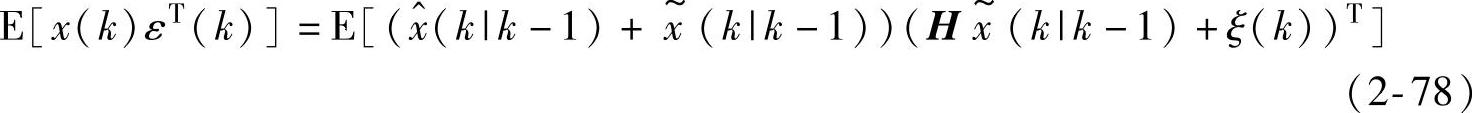
由投影正交性,有

且注意 、
、 ,于是由式(2-78)引出
,于是由式(2-78)引出
E[x(k)εT(k)]=P(k|k-1)HT (2-80)
将式(2-80)和式(2-77)代入式(2-52),得增益式(2-47)。
证毕。
注解2.1 初值取式(2-50)是为了保证估值的无偏性。采用式(2-37)、式(2-38)、式(2-45)、式(2-62)得到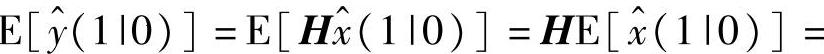

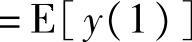 。当k>1时,进一步得到
。当k>1时,进一步得到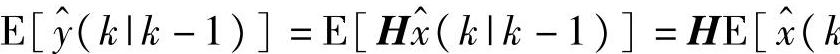
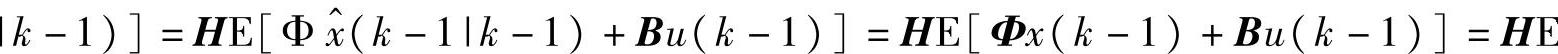 [x(k)]=E[y(k)]。因此,对所有k>0,E[ε(k)]=0。合并式(2-44)~式(2-46)得到
[x(k)]=E[y(k)]。因此,对所有k>0,E[ε(k)]=0。合并式(2-44)~式(2-46)得到
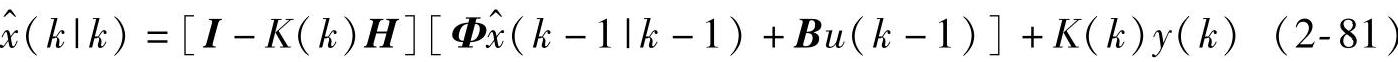
考虑例2.1,取 ,P(0|0)=1,注意ΓQ1/2=0,取R=1,则得到与式(2-4)等价的解,具体求解步骤为
,P(0|0)=1,注意ΓQ1/2=0,取R=1,则得到与式(2-4)等价的解,具体求解步骤为
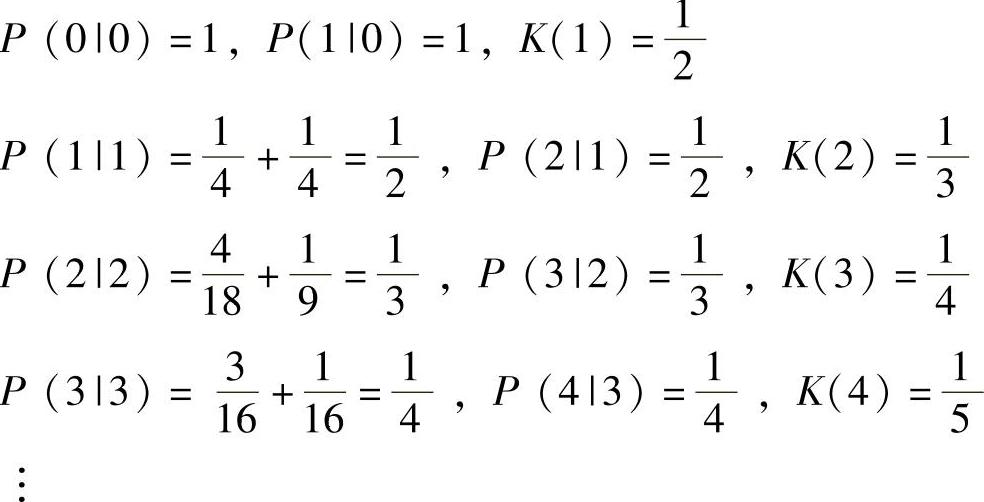
例2.2 考虑系统 ,y(k)=[1 0]x(k)+ξ(k),Q=1,R=2,
,y(k)=[1 0]x(k)+ξ(k),Q=1,R=2,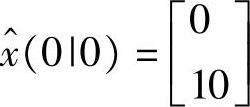 ,P(0|0)=diag{2,3},y(1)=9。由定理2.5可得
,P(0|0)=diag{2,3},y(1)=9。由定理2.5可得


例2.3 考虑系统
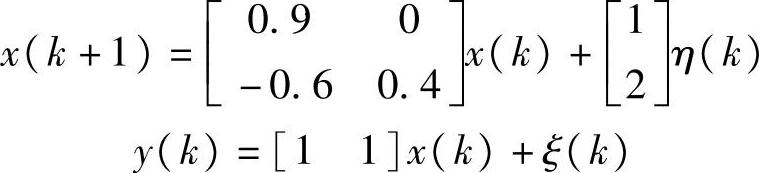
其中,x=[x1x2]T,η(k)和ξ(k)是方差各为0.81和1的独立高斯白噪声,问题是求Kalman滤波器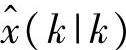 。取初值为
。取初值为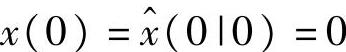 ,P(0|0)=0,仿真结果如图2-1所示,其中,实线为真实值,虚线为估值。
,P(0|0)=0,仿真结果如图2-1所示,其中,实线为真实值,虚线为估值。

图2-1 状态x(k)和Kalman滤波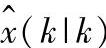
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




